tから学んだこと
「さらが 5まい あります。1さらに りんごが 3こずつ のって います。りんごは ぜんぶで 何こ あるでしょう。」(《問い》)という出題に対し,(略)
これですが,《問い》は次のアレイ図に対応するというのが,算数教育に携わる者の間の共通認識になっていると思われます.
決して,次のアレイ図ではありません.
(略)
このように「一つ分の大きさ」と「幾つ分」を捉えることができるかを確認するよう,デザインされ,出題されています.別の言い方をすると,初めに挙げた図のように認識することが,出題に組み込まれているのです.
りんごのかけ算
66ページの要所を,3項目にまとめることができます.
- 「具体物をまとめて数える」と題した,第1学年向けの授業例です.
- 「子どもが3人います。みかんを1人に2こずつあげます。みんなでなんこいりますか」を出題しています.
- 「1個ずつ置くか,2個ずつ置くかという置き方ではなく,置いた結果に着目させる」を,指導上の留意点として挙げています.
「かけ算の順序」のダブスタ考
工学的な言い方をしてみると,立式時にコストをかけておく(教育者・学習者にかけさせる)ことで,「立式」と「計算」を分離をするという利得があるということです.
この“分離”は,プログラミングに携わる者として「疎結合」を連想します.日本では「一つ分の大きさ×いくつ分=全体の大きさ」,他国では「いくつ分×一つ分の大きさ=全体の大きさ(に相当するその国での言葉の式)」を,立式時に適用できるルールにそれぞれ入れておけば,国内外での式表示の違いを吸収でき,『坪田耕三の算数授業のつくり方 (プレミアム講座ライブ)』のいう「式は世界共通」「式の裏に隠れている文化は違います」(p.138)に納得できるわけです.
こうして場合分けをしていくと,「5×2=10を正解とするための理路」が見えてきます.「1あたり量×いくつ分=全体量」のみでは,不正解となり,これが「かけ算の順序は数教協も守っている」という主張の背景になります.そこに,遠山が著したトランプ配りか,『かけ算には順序があるのか』に記載されている法則・手法を加えることで,正当化できるわけです.
Towards Japanese Multiplication Instruction
- "If the multiplication is identified, then we do not need the distinction between a multiplicand and a multiplier." --- The identification is much harder than you think because the choice of operation is a well-known issue in math education. Even limited to the multiplication, the way of recognition like that would disable children to choose two factors accurately in an infoglut situation, say "You are going to buy 4 bottles. Each bottle contains 280mL of juice and costs you 136 JPY (Japanese yen). How much do you have to pay?"
なぜ教材研究
- 教材研究をせずに先生が授業をすると,教科書などの読み上げや,ドリルなどを解かせることに終始してしまい,子どもたちに,個別の問題を解くことや算数的な活動の意義が見出せないように思います.
算数教育そして教材研究から離れて,類例を挙げてみます.
- コーディングにおいて,他で見つけたコードをチェックせずに取り入れると,前提条件が異なるためバグが発生する可能性があります.また稼働後にライセンスの問題が発生し,金銭的な損失や対外的な信頼の低下が発生するおそれもあります.
- 本を,書かれているままに受け入れると,だれのどの主張も正しいということになってしまいます.
- あっちのゼミで発表したスライドそのままで,こっちのゼミで発表すると,聞き手は訳分からないという顔をすることになります.
ななめ
ポイントは,長方形の面積を縦×横の公式に適用して求める場合,「縦はどれであるか」ではなく「縦をどこにするか」を問うことです.発見ではなく選択,と言ってもいいでしょう.そして,縦になる辺を選択すれば,横の長さは確定します.
算数ものづくり
これらの情報から,「わる数とわられる数に同じ数をかけても,同じ数で割っても商は変わらない」は,最新(2008年)の学習指導要領で取り込まれたことが見て取れます*2.
*2:さらに言うと,「分数のわり算では,わる数を逆数にしてかける」といった形の記述がありません(現行ではp.194で計算事例の中で,その操作を見ることができますが).言い方を変えると,「分数のわり算で,わる数を逆数にしてかけるのはなぜか?」の答えを得たいとき,学習指導要領を読むだけでは不十分で,他の解説書や多くの計算をもとに,学ぶ者として納得する(子どもらに理解させる)必要があるということです.このことは,「かけ算の順序」においても,留意すべき点のように思えます.
アレイ図
「じゃあどうする」に対するよい結論,言い換えると一本化は,難しいようにも思います.アレイ図が与えられたとき,どんなかけ算の式と結びつけられるかについては,状況によって異なります.いろいろ目にしてきた限り,日本の小学校では,「1種類(縦×横)」「2種類(縦×横,横×縦)」「多数」が,その状況に合わせて採用,使用されています.
海外では,Webでざっと見た印象として「1種類(縦×横)」が多く,ついで「1種類(横×縦)」で,2種類以上というのは見かけませんでした.
4マス関係表
問題にならない,言い換えると混乱しにくいのは,おそらく,2×2の表だけで見るのではなく,そこに,矢印と「×数」「÷数」を添える点にあるようです.
(略)水やりをする面積が一定のとき,(手分けして)水やりをする人数と,水やりに要する時間には,反比例の関係があるというのを前提としています.
ということで,テープ図を描くなど,4マス関係表にする前の段階で「いつもと違う(比例ではない)」と見抜けますし,3人で12分,4人だと1分と求めてから,「あれ,おかしいぞ」と気づけるよう,数量の感覚を養っておけばいいわけです.
算数ものづくり2 - 授業研究における指導案とは
指導案を改善していく試みは不可欠ですが,完璧なものを目指すのにはなじめません.料理のレシピを連想します.作る人も味わう人も,時代の流れで変化しますし,キッチンもお皿も,レシピどおりとはいかないのです.
「かけ算の順序」と算数教育をより深く理解するための3つの四字熟語
こういう区別もできます.教材研究のゴールは,類題と比較してその教材や出題の意義を見出すことです.一方,授業研究は,上下学年を含む他の学習内容との連携も必要となり,児童・(一般的な意味での)学習に対する理解と相まって,より高度なものが要求されます.
長方形の面積,数直線でかけ算わり算
とまあ書きましたが,学校教育としては,単位正方形の個数から,「長方形の面積=たて×よこ」を公式とし,「よこ×たて」でもいいよねと確認して,平行四辺形の面積の公式へともっていくのかなと思います.「かけ算の順序」の件と同様に,「面積の式はね,外国では…」と話すネタにもなりそうです.
Shampoo Boy
感謝です.で,リンク先を一通り読みましたが,どちらかというと,問題文中の2つの数値の“出現の順序”として,使用しているように見えます.啓林館の「児童は数値の与えられた順に立式してしまう(4×5とする)ことが多い」のところだけは,式の順序と読むこともできますが,これも問題文中の数値の出現順という意味合いが無視できません.
- 「ここに4まいのふくろがあります。かずや君が,1まいのふくろにりんごを3こずつ入れました。りんごは,ぜんぶでなんこありますか。」に子どもが「4×3」と書いたらバツとし,正解は「3×4」だ,これがかけ算の意味なのだという指導
に反発する一方で,
- 当雑記の2012年3月8日(九九する究めるハックする・4. 式と図)は,それがどのような背景・意図で出題され,正答率が算出されているのかを示すために書いたのに対し,「誤読」と言い,「いくつ分×1つ分の式を間違いとする教え方は間違っているのではないか」を論点にすること
は,新たなダブスタであるように見えます.
8マス関係表
興味深いのは斜めの方向です.この種の表で,斜めは通常,関連が薄いのですが,これに関しては,斜めに見るのにも意義があります.何かというと,
- さらが 5まい あります。1さらに りんごが 3こずつ のって います。りんごは ぜんぶで 何こ あるでしょう。
と
- 1さらに りんごが 5こずつ のって います。そのような さらが 3まい あります。りんごは ぜんぶで 何こ あるでしょう。
は,「5」が先,「3」が後に出現している,という共通点があります(残りのペアは,「3」が先,「5」が後です).
2つの数の出現順は同じだけれど,りんごの個数・さらの枚数に注意すると,それぞれ異なる場面というわけです.
教育者,経験的科学者,学者的哲学者
- 教育者の伝統:教師の行動の体系化,教師重視
- 経験的科学者の伝統:量的研究および質的研究,学習者重視
- 学者的哲学者の伝統:論理的な分析,教師・学習者から距離を置く
0にかける,0をかける
「かけ算の性質を利用する」を採用するとき,次のようにするのが,誤解を生じにくいように思えます.
- 3×1(被乗数は,1から9までならどれでもいい)から3×5あたりまでとその計算結果を書く.
- 「乗数が1増えれば積は被乗数分だけ増える」ことを確認する.
- 逆方向から見て,「乗数が1減れば積は被乗数分だけ減る」ことを確認する.
- 3×1の式の上に3×0を書いて,この式の答えは何とすればいいかを問う.
- 3×0=0を,みんなで共有する.
本から学んだ「かけ算の順序」ツアー
この出題で期待されているのは,つばさが6×2,あおいが2×6ということなのでしょう.
そして,まとめとして引き出したいのは,“かけ算の式で表すときは,問題文から「1つ分の大きさ」と「いくつ分」を見つけるようにする”だと思います.
これを見たとき,こういう反論もできそうです.“このように,ペアで与えられた場合には,書き分けるのに賛成するが,このうち一方しか出題されなかったら,交換法則やトランプ配りを使って,どちらのかけ算の式でもよい”です.
この種の対立は,「かけ算の順序論争」のいろいろなシーンで,見ることができます.そこはどちらが教育的であるか,学習者である子どもたちに配慮されているか,でもって,先生方そして学校が選択していただくしかないのかな,と思っています.
問題と解答の展開
- 学校教育では,8つのうち,《被順》と《乗逆》になる4つだけを,正解としています.
- 文章題をもとに,かけ算の式を書く授業やドリルでは,《乗》からではなく《被》から始まります.《乗》は,途中で意図的に出題されます.
数学と教育の協同
バスが数学者,ボールが現場教師(教育実践家)です.推測ですが,教師は,たとえ児童が授業で,間違いをしていると即座に気づいても,「どうしてそうなるの?」と尋ねます.対話して,言葉を引き出していきながら,「そうね」と共感します.それから,正解を得るにはどうすればいいかを確立していきます.その際の教師・児童の対話は,必ずしも一対一ではなく,先生のコントロールのもとで,他の児童の発言が差しはさまれることもあるでしょう.
このとき,教師の言う「そうね」は,正しい答えに持っていくための,スイッチとなる言葉となります.そう言うのが,朝起きたときに「おはよう」と言う,通夜に駆けつけたときには「ご愁傷様です」と言うのと同じくらい,ボールにとっては当たり前のこととなっているわけです.
児童によるつまづきと,それに対するボールの対応---必ずしも「そうね」と言っているかは分かりませんが---をいくつも,ビデオ(もしかしたら実地でも)で見たバスは,「だって, あなたは何でも正しいことにしてしまうんだ」と言います.これによって,数学者(バス)の感じる魅力と教師(ボール)のそれとが異なることが,明らかとなったわけです.
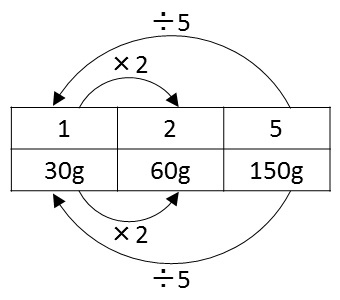
2×30g
さてこの2人の考え方は,表を作って関係を添えると,違いが明確になります.男の子のプロセスは,次の表になります.
4マスではなく6マスですが,「1と5の列」と「1と2の列」の2つの4マスをくっつけた次第です.
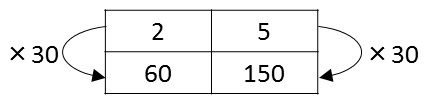
女の子の表は,次のとおり.
「2」と「5」は無次元量で同じ種類の数なので,上の行に書き,「60」と「150」は重さでこれまた同じ種類とできるので下の行に置きます.
黒板の「小麦粉の比に×30をすると150になります」は,5と150という上下を見たときの関係を言っているわけです.(略)
評価と設計
前々から気になっていたのは,ここで関心を持っている文章題が,“診断的評価”“形成的評価”“総括的評価”の順で,子どもたちに出題されているわけではない,という点です.
より具体的にいうと,“診断的評価”としては,その文章題は3年のかけ算の単元のところで現れます.すなわち,2位数に1位数をかけるだとか,被乗数または乗数が0の場合だとかいった,九九より広い範囲でも,かけ算が使え計算できるというのを学習していく前に,2年のかけ算のことをきちんと理解しているか,忘れていないかを確認するために,出題しているのです.
その一方で,教育評価とシステム設計の共通点,そして“3点セット化”の意義として,次のことを挙げたいと思います.すなわち,何らかの出題や,システムの技術的な要素を見たときに,「ああ,それはあそこのことだな」と,全体からの位置づけが推測できるのです.何か改善・解消したい状況であれば,“問題の切り分け”と言ってもいいでしょう.
Towards Japanese Multiplication Instruction Using Array
Although the children need not learn Cartesian product, the usage of sets is closely related to the modernization of math education. The modernization brought just a decade enthusiasm and confusion, I suppose. However the arrays survive now, as a tool for understanding the multiplicative structure.
筆算の順序
C2さんの疑問を,大人モードで表すと,こうです:分配法則を使って42×3=40×3+2×3=120+6=126になるのだけれど,なぜ「4×3」「2×3」ではなく,「3×2」「3×4」とするのでしょうか.
回答するなら,「かける数・かけられる数がいろいろ変わっても,計算しやすく,混乱(間違え)にくくするため」というのが良さそうです.
- 筆算ではかける数なのに,内部計算の九九だとかけられる数にしているのは,その段の九九だけで答えを出せばよいからです.
- 下の位からかけていき,足していくのは,繰り上がりがあるような筆算に対処しやすいからです.
包含除と等分除 再考
結論として,歴史的にも国際的にも,初等教育における除法には,2種類の意味づけがあると言っていいでしょう.
加えて,現在の日本の算数教育では,「言語活動」「算数的活動」のウエイトが高まっています.そうしたとき,ある出題(文章題,場面)に対して,子どもたちが答え(個数,人数など)だけ,あるいは式と答えだけを書くのでは不十分であり,その判断・根拠を説明できるようになることまでが期待されています.包含除と等分除の区別は,演算決定の根拠をより明確にし,算数(数学)と日本語を結びつけたコミュニケーションを図りやすくするのに寄与すると言えそうです.
被乗数先唱 俺流まとめ
- Q: 海外では,かけられる数とかける数が日本と反対になります.日本の算数も,「かける数×かけられる数」になっていくのでは?
- A: 「たされる数+たす数=和」「ひかれる数−ひく数=差」「かけられる数×かける数=積」「わられる数÷わる数=商」として四則演算を見ると,基準量となるものを,演算記号の左に書くことにすれば統一がとれ,合理的です.なので,「かけられる数×かける数」を支持します.(略)
被加数・加数の順序
YESなのは,「かけ算の順序論争」の知見が使えそうな点です.すなわち,
- 乗法に〈乗数と被乗数が区別される文脈〉と〈乗数と被乗数を区別しない文脈〉があるのと同様に,加法にも〈加数と被加数が区別される文脈〉と〈加数と被加数を区別しない文脈〉が考えられます.
- 〈加数と被加数が区別される文脈〉は「増加」(または「添加」),〈加数と被加数を区別しない文脈〉は「合併」という名称で,算数教育の場で十分に普及しています.
- ただし,加法は〈加数と被加数を区別しない文脈〉から先に学習するのが良いとされています.乗法が〈乗数と被乗数が区別される文脈〉から先なのと対照的です.
「7+5=12は△,正解は5+7=12」の件
この問題は,算数教育においては「逆思考」の問題と呼ばれます.「のこりは」とあるけれども,ひき算ではなく,たし算の式を書いて求めるのですよ,というものです.
小学校学習指導要領解説 算数編では,以下のとおり,これに関連する例題が記載されています.
- 「はじめにリンゴが幾つかあって,その中から5個食べたら7個残った。はじめに幾つあったか」(p.96,第2学年)
- 「はじめにリンゴが幾つかあって,5個もらったら12個になった。はじめに幾つあったか」(p.97,第2学年)
- 「ひもを4等分した一つ分を測ったら9cmあった。はじめのひもの長さは何cmか。」(p.107,第3学年)
期待される式はそれぞれ,7+5=12,12−5=7,9×4=36です.2番目に現れる数が,式では最初(被加数,被減数,被乗数)に来る,という規則があるわけではなく,文章題で書けばそういう流れになるのが自然なのでしょう.
小学校の算数には数学がないのか
日本で「順番は関係がない」という主張が普及しているのは,
- 数学教育協議会を結成した遠山啓の考え方や,「トランプを配るときのやり方」を含む記事を信奉しているから
- 学校教育に対して信頼を置いておらず,何かあったら追及したがるから
あたりのほうが大きく寄与していると思っています.
(略)「算数≠数学?」については,次のように考えています.同じか違うかで言うと,違います.それぞれを1次元あるいは多次元の数量ではなく,集合としたとき,算数∩数学=∅ではないのも,また確かでしょう.すると,「算数にも数学にもあるもの」,「算数にあって数学にないもの」(加える「何か」),「数学にあって算数にないもの」(引く「何か」)を,追究したくなるのです.