1. 俺教材研究2
教科書にある,「いくつ分」×「1つ分の数」の実例 | メタメタの日に対して,はてブしました.
見直すことにします.ちなみに前回の「俺教材研究」は去年の8月2日です.
(1) あまりのあるわり算
「76まいの色紙を,3人で同じ数ずつ分けます。1人分は何まいになって,何まいあまりますか。」という問いから始まります.1人分は25まいで,1まいあまる,になるのでしょうね.
筆算をすると,商は25で,あまりは1です.そして教科書には,「3×25+1=76」という数式と,「わる数×商+あまり=わられる数」という言葉の式があります*1.「3×25+1=76」という数式の「3」は,「76÷3=25あまり1」という式の中の「わる数」です.「25」は「商」,「1」は「あまり」,「76」は「わられる数」です.このようにして(本当はもっとたくさんの出題でたしかめられるといいのだけど,時間の都合で)「わる数×商+あまり=わられる数」という言葉の式を得ました.…
いえいえ,話は,完結していません.「3×25+1=76」って何でしょう?
教科書には等式が書かれていますが,右辺を無視して,左辺の3×25+1だけを見て,計算することにします.3×25+1=75+1=76です.ここで3×25の筆算をさせ,76÷3の筆算と見比べると,「15」と「6(60に相当)」が共通して現れる*2点も,押さえておきたいところです.ということで,教科書ではいきなり等式ですが,ここは右辺を隠して,左辺だけで計算し,隠した「76」になることから,「3×25+1=76」をたしかめるようにしましょう.
ところで,「3×25+1=76」のところは,「25×3+1=76」としてはいけないのでしょうか.
「25×3+1=76」だと,「76まいの色紙を3人で分けたとき,1人25枚ずつの色紙を持ち,1まいあまります」という場面を表します.そして,「20×3+16=76」ともできます.「76まいの色紙を3人で分けたとき,1人20枚ずつの色紙を持ち,16まいは(例えば,色紙入れに入っていて)だれのものでもありません」といったところでしょうか.「あまり」「あまった」はわり算を連想するので,ここでは使わないようにします.
それに対し,「3×25+1=76」すなわち「わる数×商+あまり=わられる数」については,「あまりがわる数より小さくなる」という制約がつきます.なので,「3×20+16=76」にはなりません.その制約は,「25×3+1=76」や「20×3+16=76」という表し方では出て来ないものであり,わり算特有の面白い(でも難しさもある)性質に思えます.
教科書外の情報に当たってみましょう.学習指導要領では第4学年A(3)ウで「除法について,被除数,除数,商及び余りの間の関係を調べ,次の式にまとめること。(被除数)=(除数)×(商)+(余り)」とあります.wikipedia:除法には「m=qn+r」という式で,商が先,除数が逆の積の表記です.そういえば中学ではa=bq+rだったかな.しかし中学校学習指導要領解説数学編には,記載がありません.wikipedia:Division_algorithmでは「a=bq+r」と書いていますが,あとの文章を見ると「a=qb+r」という書き方もあります.どちらでもよさそうですが,ここは教科書と学習指導要領に合わせておきましょう*3.
ところで最初の問題は,等分除です.包含除だと例えば…「76まいの色紙を,3まいを1セットとして分けます。何セットできて,何まいあまりますか。」となります.わり算の式は「76÷3=25あまり1」,たしかめは「3×25+1=76」と,同じです.包含除でも同様に,あまりを含む場面で適用すると,「わる数×商+あまり=わられる数」が成り立つわけです.
ただしこの場合には,かけ算ベースでも「25×3+1=76」や「20×3+16=76」という式にはならないところもまた,興味深いものです.って,授業でここまでできる時間はあるかな?
(2) 4人のならび方
「Aさん,Bさん,Cさん,Dさんの4人の子どもがいます。4人がならぶと何通りのならび方があるか考えましょう。」という問いから始まります.
□×□×□×□は,4×3×2×1ですね.「1番目は4人のうちの1人を決めるので,4通りの決め方があるね。2番目は,その1人に対して3通りの決め方があるね。ということは,2番目までは 4×3通り あるんだね。」という,あおいさんの考えが吹き出しになっています.
これは,「Bを『基準にする大きさ』,Pを『割合』,Aを『割合に当たる大きさ』とするとき,B×P=Aと表せる。」(《算数解説》p.166)で,B=4,P=3*4として,A=B×P=12と考えるのがよさそうです.教科書では,「基準にする大きさ」「割合」「割合に当たる大きさ」のことを何と書いてたっけ…*5.
1番目だけだと4通り.2番目を書くと,1番目と2番目の並び方は12通り.これが「4×3通り」です.4通りが3倍で12通りになった,という言い方もできそうです.
3番目は,2番目までの並び方が2倍になるので,24通り,「4×3×2通り」と書けます.
4番目を入れると,かけるいくつかな…なのですが,1番目,2番目,3番目を選ぶと,4番目はただ一つに定まります.これは,樹形図を描いたときに,3番目と4番目の線がどれも1本ずつ(1対1対応)ということからも分かります.「1倍」として,「4×3×2×1」が,求めるための式です.
表にできますね.
| 1番目まで | 2番目まで | 3番目まで | 4番目まで |
|---|---|---|---|
| 4通り | 12通り | 24通り | 24通り |
| 4 | ×3 | ×2 | ×1 |
ここで,「1×2×3×4」または「2×3×4」とすることはできないか,考えてみましょう.
1番目がAとなる,4人のならび方は,樹形図から分かるように6通りです.この6を「一つ分の大きさ」とし,1番目がBのときも,Cのときも,Dのときも6通りなので,「幾つ分」を4とすれば,6×4です.
1番目はAというのを固定します.それで,2番目がBという,4人のならび方は,2通りです.2番目がCのときも,Dのときも,2通りなので,「一つ分の大きさ」を2,「幾つ分」を3(B,C,D)とすると,2×3=6です.
これは,24→6×4→2×3×4をやっているように見えます.ちょっと子ども向けではなさそうです.
因数を「4×3×2×1」という降順にすべきか,「1×2×3×4」という昇順にすべきか,というのは,確認しておきましょう.今回の問いでは「4×3通り」という書き方から,降順が期待されているようです.人数を変えて,「Aさん,Bさん,…,Jさんの10人の子どもがいます。その中から4人がならぶと何通りのならび方があるか考えましょう。」という問題文だったら,10×9×8×7という式にしたいところです.昇順だと,最初が6か7か迷いそうです.再度Wikipediaを引くと,wikipedia:順列もwikipedia:階乗も,降順ですので,高校数学との連携という面でも,このほうがいいのでしょう.
(3) 俺教材研究2・まとめ
- 思ったことを書き出しましょう.
- その中から,授業で子どもたちに引き出してもらいたいことを発見・確認しましょう.
- 教える側が言うべきこと(発問,アドバイスなど)を,言うタイミングとともに押さえておきましょう.
- 類題を作りましょう.
- 他の情報源と照合しましょう.
以下しばらく「教材研究」から離れます.ちゃんとオチはつけますので,どうかお忘れなきよう.
2. 「掛け算順序固定」問題対策本部について
年末に,- 「掛け算順序固定」問題対策本部 - アットウィキというのができました.日々,コンテンツ追加や内容の見直しが図られているようです.私のエントリにもリンクされています.いくつかは,こちらから要望しました.
さてその中の,「アレイ・グリッド (AG)モデル」「ターゲット・オペレーション (TO)モデル」(- 「掛け算順序固定」問題対策本部 - アットウィキ),「アルイメージ(RI)解法とテキストパターンマッチング(TPM)解法」(- 「掛け算順序固定」問題対策本部 - アットウィキ)といったラベリングから,米国式の改革が根底にあるように感じました.
「米国式の改革」とは,次のことです.
この改革運動において米国数学教育学会が取った方策は,米国における改革に共通して見られる方法の具体例であると言えます。専門家が招集され,教職に関する研究と実践とを調べ,改革に向けた勧告を作り上げます。このような勧告は文書のかたちにされて広く配布されます。それらの文書の一つ,米国数学教育学会の「算数・数学科学習指導の専門職的基準」は,児童・生徒の学習水準の向上のためになぜ学習指導の変革が必要であるかについて,かなり明確に述べています。米国数学教育学会が描く変化は本質的なものです。
(『日本の算数・数学教育に学べ―米国が注目するjugyou kenkyuu』p.102)
その結果,教師の理解度調査は「知っている」の回答が高いものの,ビデオ撮影した授業を分析する限り,授業にはほとんど生かされていない,という展開です.
飛び飛びですが,次の2つの記述が目を引きます.
学習に関する長期的にわたる改善のかわりに,限られた特性とか活動によって学習指導の成功を定義するためにこのようなことが起こるのです。このことが生じるかぎり,改革論者が最善のものとして提示した計画は期待に反した結末を迎えます。
(p.104)
米国の教科教育学者は大きな変化を比較的短期のうちに求めてきました。実際,正にこの「改革」という言葉は突然の大規模変化という意味を内包しています。これに対して,日本の教科教育学者は,学習指導に関する長期にわたる漸進的,微小増加的改善が生じる方式を制度化してきました。この方式は明確な学習目標,全国的に共通なカリキュラム,および授業実践における漸進的改善に立ち向かう教師の勤勉,努力を含むものです。
(p.106)
とはいえ,違いもあります.開米瑞浩氏([twitter:@kmic67])は算数・数学教育の専門家ではなく,「研究と実践とを調べ」ている形跡もありません.
形跡がないと判断している根拠を,2つ挙げておきます.まず,「TPM解法」についてですが,そうならないよう指導をすべきことが,算数教育のいろいろな本に記載されているのに,そういうのを踏まえた書き方ではないのです.
手元にある本の中から,書き出してみます.
文章題は時間がかかっても、問題はノートに写させます。写しながら読み取る力がつきます。次にキーワードとなる言葉や数字に線を引かせます。そのときに気をつけないといけないのは、
- 「もらう」「みんな」「来る」「あわせて」「買う」「多い」…加法
- 「あげる」「使う」「残る」「取る」「少ない」「食べる」…減法
というように、これらの言葉だけで演算決定しないことです。
(『まるごと2年生 2年生担任が まず読む本 (教育技術MOOK)』p.18)
学習指導要領の解説では,「〜してはいけない」という形をとりませんが,例題と考え方を示しています.
(1)数量の関係表現は減法の形であるが,計算は加法を用いることになる場合
例えば,「はじめにリンゴが幾つかあって,その中から5個食べたら7個残った。はじめに幾つあったか」を求めるような場合である。図で表せば,次のような場合で,□を7+5として求める。
(テープ図:省略)
………
式を用いて説明するに当たっては,例えば(1)の場面であると,「幾つかあるリンゴから食べたリンゴの5個を取ると7個残る」ということから,残った7個に取った5個を返す(たす)と7+5という式になるというように,式の部分である「7」,「+」,「5」と場面とを関連付けて説明することが,また,そのことを(1)で示したようなテープの図とも関連付けて説明することが,加法と減法の相互関係について理解し,式を用いる能力を伸ばすために大切である。
(《算数解説》pp.96-97)
なお「5+7ではいけないのか」については,今回の本題ではありませんが,9月12日に書いています.
「形跡がない」の2点目ですが,「アレイ・グリッド (AG)モデル」「ターゲット・オペレーション (TO)モデル」については,当雑記の「積指向」「倍指向」と認識が似ています.そして積指向についての課題も,文献から知ることができます.
《積指向》による,数学的な定義や数学教育の書籍は,目にしていません.ないわけではなく,もう少し具体的に書くと,《積指向》で乗法を導入して,成功しているという事例・書籍は,見かけません.その一方で,国内外の専門家が,次のように指摘しています.
累加の考えをさけようというのは,算数の指導についての基本的な立場の相異によることであって,乗法という問題だけで考察することは適切とはいえない.(略)しかし,乗法と加法の特別な場合を簡潔に表すという立場から意味づけることは,とくに,低学年の場合には,教育的にも意味のあることであり,さきのラパッポルト氏の反論にもある.
わが国でもこの立場をとっているが,アメリカの新しい計画による教科書でも,この立場をとっているものが多い.これには,ラパッポルト氏の指摘にもあるように,整数の段階では,集合の直積に近い意味づけをしても,累加の考えに帰著してほぼ処理できることや,直積の考えのままでは,実際に乗法を適用するに当たって,困難をともなうことなどの理由があげられよう.
([中島1968b] p.76)The Cartesian product is so nice that it has very often been used (in France anyway) to introduce multiplication in the second and third grades of elementary school. But many children fail to understand multiplication when it is introduced this way. The arithmetical structure of the Cartesian product, as a product of measures, is indeed very difficult and cannot really be mastered until it is analyzed as a double proportion. Simple proportions should come first.
([Vergnaud 1983] p.135)This class of situations corresponds to the formal definition of m × n in terms of the number of distinct ordered pairs that can be formed when the first member of each pair belongs to a set with m elements and the second to a set with n elements. This sophisticated way of defining multiplication of integers was formalized relatively recently in historical terms.
([Greer 1992] p.277)中国の教科書で被乗数と乗数の区別を廃止したという例がありますが,[国教研2009] p.181には以下のように書かれており,簡単ではないことがうかがえます.
「倍」と「積」から学んだこと 10.《倍指向》と《積指向》には,起源,または数学的な裏付けがあるのでしょうか?乗法の学習は第2学年上半期に九九に伴って始まる。1つ前の教育課程から, 「一部分の学習者が被乗数と乗数の区別に難儀を感じる」,「中学校に入ったら被乗数も乗数も因数として扱う」などの理由で,被乗数と乗数の区別をなくし,最初から因数として扱うこととした(略)。これについて現場の授業等を観察したことがある。この処理は数計算の場合大きな差支えがないかもしれないが,量の扱いではやはり不具合があって,教師たちの丁寧な対応によって乗り越えているところである。
ちなみに個人的には,これらの記述をもって「AGモデル」「積指向」がダメだ,とは思っていません.その認識を算数教育で採用すると,困難な点が多いことが,先人の著書・刊行物に記されているのです.加えるなら,当該エントリ作成者はその書き方から,認識をしているようには見えません.それでもなお,AGモデルをメンタルモデルの一つとして掲げる,すなわちかけ算(そして算数)の学習や指導において理解しておくべき概念であると主張していくのなら,プラスアルファを期待したいのです.
あと,アレイ(長方形的配列)による表現は,「数学教育の現代化」と関係します.現代化は,昭和43年改訂の小学校学習指導要領に色濃く反映され(例えば,教科書いまむかし 数学教育現代化時代(小学校) -大日本図書-),批判を浴び(教科書いまむかし 基礎・基本の時代(小学校) -大日本図書-),その次の改訂では削られたという経緯もあります.
そういった歴史を踏まえた上での「AGモデル」であるように見えないのです*6.「TPM解法」も同様です.そんなので,コンテンツをどんどん作っていったとして,それが算数・数学教育に携わる人々にどのように役立つのだろう,カーゴ・カルト・サイエンスにならないのか,という思いを抱かずにはいられないのです.
3. 「4つの質問」に回答
- 「掛け算順序固定」問題対策本部 - アットウィキに,回答してみます.
小学2年生へかけ算を教えるときの、式の順序は「1あたり×いくつ分」に固定すべきである、という立場の先生へおたずねします。
「1あたり」は好みでないので,「一つ分の大きさ」に読み替えます.それと「に固定すべきである」のところは「は導入時には適切だし,乗法の適用対象の拡張や,日常生活での活用においても,この考え方は有用だ」と理解しています.あと,「式の順序は」も取り除きます.
Q1 :「掛算の式には正しい順序があり、それは 大人になっても同じ である」と考えますか?
回答:NO.
まず,「掛算の順序」という言葉は,曖昧である上に数学教育学において議論が見られず,「マイナスイオン」と同様に駆逐されるべきだと考えています.
「一つ分の大きさ×いくつ分」は,かけ算の式で表せる方法(十分条件のようなもの)の一つに過ぎませんので,長方形の面積の公式や,上に書いた(回答文よりも前です)「B×P=A」など,別のかけ算の式が利用可能なときは(公式は導くか,信頼できる情報源を根拠に),それを使うだけのことです.
なお,以下の絵と式(『まるごと2年生 2年生担任が まず読む本 (教育技術MOOK)』p.16)のように,被乗数と乗数に書く数を区別したいという状況はあるでしょうし,その際には,「一つ分の大きさ」をかけられる数にするというのを小学校のときから学んでおくと,コミュニケーションが円滑に進むと思われます.

Q2 :「2×8なら答の16はタコの匹数になってしまうことをおさえる」 とする教え方を肯定しますか?
回答:YESでもNOでもありません.
2×8という式から,かけ算の式にするにあたり,タコの匹数と足の数を取り違えたんだなと考えます.それを面白おかしく分からせるために,「(それだと)タコの匹数になってしまう」と指導しているのでしょう.
Q3 :「2×8ならタコ2本足」という教え方を肯定しますか?
回答:YES.
より具体的には「2×8だとタコ2本足と思われちゃうよ(君がそうじゃないという明確な意図をもって書いたとしても)」です.
書いた人がどう考えたかよりも,そう書いたらどう受け取られるかに注意します.
なお,Q2とQ3では,2×8という式に対する解釈が異なっています(Q2では一つ分の大きさが「タコ2匹」なのに対して,Q3では「タコ2本足」)が,これについては『板書で見る全単元・全時間の授業のすべて 小学校算数2年〈下〉』pp.46-47に先例があり,個人的にも12月27日に考察を試みています.
Q4 :遅くとも小学校卒業までに掛算はどちらの順序でも正しいことを教えるつもりはありますか?
回答:NO.
ある状況では,一つの式が正しくなる(ように,既習事項をもとに授業やテストで出題している)し,別の状況では複数の式や考え方があり得るというだけの話です.
そのことは問題集や学習指導案をいくらか読めば,小学校教育の素人であっても確認でき,「掛算の順序」に類する言葉が出る余地はありません.
上記に関する注意事項です.
- 「4つの質問」ページの内容は変わる可能性があるので,回答時に参照した質問文を引用しています.
- 当雑記ではリリース後でも頻繁に書き換えています.本エントリも,そうする可能性が非常に高いです.なので以上の回答をもし,ページ内に書いていただくのでしたら,回答文を切り貼りするのではなく,当エントリのURLを示すにとどめることを強く要望します.氏名・日時などは,つけていただいてもかまいません.
- 私は情報通信分野に関わる大学教員ですが,小学校の教育には関与していません.そういった立場から,子どもたちの教育が,より良い方向に進むのを期待しています.このことをベースとした回答であることも,ご理解ください.
4. 解くべき問題は何か?
「かけ算の順序論争」を,はたから見ている者ですが,それでも,そこで解くべき,あるいは設定すべき問題を何とすればよいのかというのは,考えてみる価値がありそうです.
直球勝負なら,「順序はあるのか,ないのか」でしょうか.某ページのタイトルを借りて,「かけ算の式の順序にこだわってバツを付ける教え方の是非」なんてのもいいでしょうね.
もう少し上のレベルにしてみると,「算数教育はどうあるべきか」「乗法に関する指導はどうあるべきか」でしょうか.
しかしここまで書いたどれについても,その答えを出すために必要不可欠な情報について,見当がつきません.また仮に,答えを出したとしても,内外に与える影響というのもよく分かりません.
しかし次のようにすれば,具体的であり,自分にも手に負える問題となります.「小学校の算数を通じて,児童が解けるようになってほしい問題は何か」です.ここで「問題」という単語の意味が違ってくるのですが,それについては後述します.
「児童が解けるようになってほしい問題」を知るための手がかりは,学習指導要領解説算数編(《算数解説》)です.例題と考え方が記されています.その知識をもとに,Webの情報や,書籍に当たり,事例や知識を増やしていきます.
この活動を通じて,到達できたことが大きく3つあります.一つは,《AB型》《BA型》《B型》《複数解》,あるいは「倍の乗法」「積の乗法」といった,「a×b=p」の式として書かせる文章題のタイプ分けです.なお,- 「掛け算順序固定」問題対策本部 - アットウィキで「倍指向」「積指向」が取り入れられ,診断チャートを含むコンテンツが大きく変わったのにはびっくりしましたが,私自身は「〜指向(=考え方)」よりも「〜の乗法(=対象)」を重視するほうが,汎用性が高いと考えています(関連:11月15日(5)).
2番目は,[Greer 1992]という文献による,乗法・除法が用いられる場合の分類(10月13日)です.12月5日にも書いています.著者であるGreer単独の貢献ではなく,そこで引用されている様々な文献の著者,そしてそのもとになっている算数・数学の指導が集約して,出来上がった文章だと理解しています.
そして最後は,自作スクリプトの99qgです.仕事算や植木算も,やろうと思えば2年生向けに出題できるのでした.
99qgはRubyで書いていますから,その仕様変更など(処理系のバージョンアップ)に応じた見直しは,頭の片隅に置いています.コンテンツ面においても,どんな「問題」をどんな形式でRubyのコードで表し,またアウトプットすればよいかというのは,限りはないけれど,“手ごろなところ”は自分なりに見出しています.もし明らかに足りないところがあると,他の方が判断されたら,githubで公開しているので,forkしてくれればいいのです.
先ほどの「問題」という言葉について.文章題は英語でword problemといいます.「問題」の訳語には,problemのほか,issueがあります.問題をissueとして見ると,
で「課題(issue)」と書いていました.これが
で取り上げられ,はてブで
- http://d.hatena.ne.jp/takehikom/20111013/1318452891
- http://d.hatena.ne.jp/takehikom/20111024/1319387411
- http://d.hatena.ne.jp/takehikom/20111115/1321302821
と推移したことを記しておきました.これは,私の頭にあるissueが変化した事例と言えます.
5. アレイ図への適用
- 「掛け算順序固定」問題対策本部 - アットウィキを最初に見たとき*7,AGモデルでは具体的な文章題を図解しているのに,TOモデルはそうでないこと,言い換えるとTOモデルは「3人に4つずつ おはじき を配りました。おはじきは全部でいくつ?」という問題を解くのに適したモデルではないという印象を与えているように感じました.
それで,

と対比するための図として
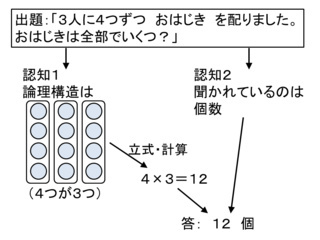
というのを描き,Twitterで報告しましたが,却下されました.その理由をもとに,
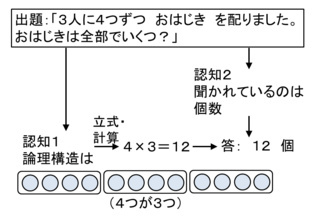
と修正してみましたが,もう連絡する予定もありませんし,採否のほどは分かりません.
なお,AGモデルが融通性において弱点を持つことは,次の図で示すことができます.アレイ図が与えられ,その○の数をかけ算の式にして求めます.倍指向,より正確には小学校の算数で学習する方法に基づけば,4通りの式が得られるのに対し,AGモデルでは,点線の2通りだけです.
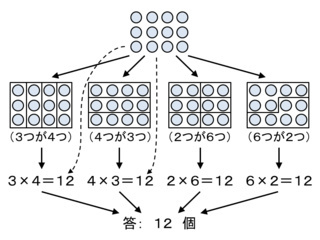
配置を変えることなく,4通りの考え方と式が得られるのは,当雑記でたびたび書いている「まとめて数える」の成果です*8.なお,「6つで2つ」の囲い込みについて,L字型でなくてもよいのですが,このような切り分け方は,合同な図形による敷き詰めに関係します.
もちろん,縦3個横4個の配置を見せてただちに「2×6」と書く子を育てたい,発見したいというわけではありません.「3×4=12」と「4×3=12」を確認した上で,「他にもあるんじゃないかな.考えてみて?」と尋ねて,引き出したいものです.
6. なぜ教材研究
教材研究とは何か,については,wikipedia:教材研究をご一読ください.なお,教材については物品にとどまらないという,wikipedia:学習材の記述に賛成です.
手元の本で「教材研究のwhy」や「教材研究のwhat」を探してみました.幸いにもwhatについては,1冊,記載がありました.
授業は指導目標の達成を目指して展開される教師,児童,教材を主な構成要素とする有機的・組織的活動である。したがって,授業にあたっては児童の実態とともに,指導目標,内容,方法を検討し,どのような展開過程で,どのような指導を行うのかを学習指導案に示さなければならない。学習指導案の作成にあたって行われる種々の研究活動を一般に教材研究という。学習指導案に示される指導目標や展開過程,学習指導法,教具,発問,板書計画などは,この教材研究をもとに決定されるものである。(略)
(『小学校 算数科の指導』pp.187-188)
「教材研究」という四字熟語が書かれている本はほかにもあって,『算数科教育の基礎・基本』(p.118),『すぐに役立つ!365日の算数授業づくりガイドブック―教師力をアップするスタンダード57』(p.9)です.上の本と合わせて,「教材研究のhow」に主眼が置かれています.言い方を変えると,教材研究という概念は,教師にとって当たり前のことであるように思われます.
上の引用で,「教材研究のwhy」も言えそうなものですが,自分なりにwhyを考えてみます.使えそうなのは,「もし教材研究をしなかったら」です.
- 教材研究をせずに先生が授業をすると,教科書などの読み上げや,ドリルなどを解かせることに終始してしまい,子どもたちに,個別の問題を解くことや算数的な活動の意義が見出せないように思います.
算数教育そして教材研究から離れて,類例を挙げてみます.
- コーディングにおいて,他で見つけたコードをチェックせずに取り入れると,前提条件が異なるためバグが発生する可能性があります.また稼働後にライセンスの問題が発生し,金銭的な損失や対外的な信頼の低下が発生するおそれもあります.
- 本を,書かれているままに受け入れると,だれのどの主張も正しいということになってしまいます.
- あっちのゼミで発表したスライドそのままで,こっちのゼミで発表すると,聞き手は訳分からないという顔をすることになります.
これだけ並べれば,長文好きな自分でも,手短に説明できそうです.教材研究とは,準備です.そして,他と対話をする前の,自分自身との対話でもあります.なぜ教材研究をするのかというと,すでにある教材・題材を,自分の中でより豊かにしたいからです.
*1:この言葉の式がもし前までのページにあれば,それを見直すことになりますが,ここが初出と仮定して,話を進めます.
*2:「25×3」の筆算だと,その仕方にもよりますが,私が小学校のときに学んだやり方では,「6」が現れません.
*3:「どちらでもいいことにしましょう」という結論にすれば,それはまた別の人の「俺教材研究」となります.
*4:ここは先生モードではなく算数教育初心者モードですが,「割合というのは0から1までの範囲なのでは?」と思って,《算数解説》を見たところ,1を超える整数も割合とみなせることが,p.142(第4学年),p.169(第5学年)から確認できました.
*5:5年の教科書を調べる必要がありますが,私は教科書を持っていないし,そもそも小学校の先生ではないので,「必要があります」とだけ書いてその作業を省きます.
*6:AGモデルに類する考え方を,アレイによる表現が教科書に登場する前から,児童ら(全員でなくてもいいので)が認識しているというエビデンスがあれば,AGモデルを検討する意義も高まるのですが.
*7:以下毒:今見ると,冒頭に太字でコメントが入っていますが,そう言うのは算数の(または小学校の)教育を通じて教師・児童が認知し共有できるイメージを十分に分類してからにしないと,教育に携わる人の賛同は得られないよなあと感じます.手元の本では,『数学教育学研究ハンドブック』の第5章が関連しそうです.
*8:《算数解説》p.65には「この活動では,既に幾つかずつにまとめられた具体物を数えるのでなく,自分で適当な大きさのまとまりを作って数えたものを整理して表すことが大切である。」とあります.たし算の式にするのなら,これは,1年生でもできるのです.