1. 長方形の面積
いきなりですが問題です．
あなたは先生(T)です．児童(C)と対話をして，次の長方形の面積を求める式と答えを書かせましょう．
ポイントは，長方形の面積を縦×横の公式に適用して求める場合，「縦はどれであるか」ではなく「縦をどこにするか」を問うことです．発見ではなく選択，と言ってもいいでしょう．そして，縦になる辺を選択すれば，横の長さは確定します．
そのことを踏まえて，解答，いや，対話例です．
T：これはどんな図形かな?
C：長方形です．
T：どうしてそう分かる?
C：問題文に，そう書いてあります．
T：あ，そうだね．それで，何をすればいいのかな?
C：面積を求めます．
T：どうやって求める?
C：長方形の面積の公式です．
T：どんな公式だっけ?
C：縦×横です．
T：ほお，じゃあ，この図形で，縦はどこにする?
C：3cmのところにします．
T：なるほど．それで，どうする?
C：そうすると，横は，5cmです．
T：そうだね．
C：面積は，3×5＝15で，15平方cmです．
T：よろしい．よくできました．
もちろん，児童が縦として（長い）5cmのほうを選択すれば，「3」と「5」が入れ替わるだけです．思考のプロセスを，図にしました．
発問という言葉を使っていいのなら，主発問は「長方形の面積の求め方（公式）は?」ではなく「縦はどこにするの?」だと考えています．そして上の対話では，直接的に「縦はどこにする?」と問いましたが，「縦はどれ?」と尋ねて，3cmと答えたら「5cmのほうじゃないの?」と揺さぶりをかけるのも，子どもによっては有効かもしれませんね．
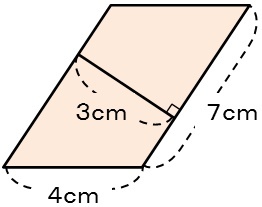
2. 平行四辺形の面積
またまたですが問題です．
あなたは先生(T)です．児童(C)と対話をして，次の平行四辺形の面積を求める式と答えを書かせましょう．
問題の出典は，平成23年度全国学力・学習状況調査として実施を予定していた調査問題の小学校算数A大問4です．
さっそくですが対話例です．
T：これはどんな図形かな?
C：平行四辺形です．
T：どうしてそう分かる?
C：問題文に，そう書いてあります．
T：ああ，そうだね．それで，何をすればいいのかな?
C：面積を求めます．
T：どうやって求める?
C：平行四辺形の面積の公式です．
T：どんな公式だっけ?
C：底辺×高さです．
T：ほお，じゃあ，この図形で，底辺はどこにする?
C：7cmのところです．
T：4cmのところじゃないの?
C：だってそうすると，高さが分からないじゃない．
T：そうか．じゃあ，7cmのところを底辺にしよう．それで，どうする?
C：そうすると，高さは，3cmです．
T：そうなるね．
C：面積は，7×3＝21で，21平方cmです．
T：よろしい．よくできました．
「解く」ならそれでおしまいですが，ちょっと対話を続けてみます．
T：でもさあ，面積が出たのなら，底辺が4cmのほうの高さも，出せるんじゃないかな?
C：21÷4，ですか?
T：そうだね．計算したら，どうなる?
C：21÷4＝5.25です．
T：高さは?
C：5.25cmです．
T：底辺×高さの公式に，当てはめてみて．
C：はい．この平行四辺形の底辺を4cmのところにすると，高さは5.25cmとなって，公式を使って4×5.25＝21と表せます．面積は，21平方cmです．
T：うん．で，この式じゃ，ダメなの?
C：この問題の，式にですか?
T：そう．
C：ダメだと思います．
T：どうして?
C：図の中に，「5.25」がないからです．
T：でも今，高さ5.25cmって出したじゃない．
C：それは，面積は21平方cmと求めていたからです．それと，4×5.25＝21という書き方だと，先に答えが21平方cmだと分かっていて，つじつまを合わせるために，5.25を持ってきたように見えるんです．
T：「見える」って，だれが?
C：マルとかバツとかを判定する人です．
T：そこまで考えてるんだね．
ところでこの問題は，全国学力テストでぽっと出てきたというわけではなく，《算数解説》p.174に説明が入っています．そこでは「底辺をどこにとるかで高さが決まること」「必要な情報を自ら選び出し面積を求めること」と書かれています．
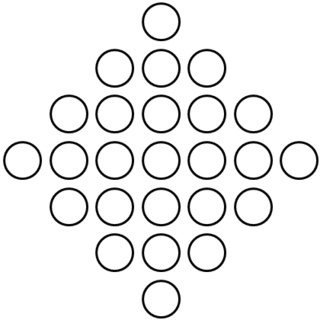
3. ダイヤモンド的配置
ここでやっぱり問題です．
おはじきが，次の図のように並んでいます．全部でいくつありますか．
かけ算を使った式と答えを書きましょう．
これも出典がありまして，『算数科教育の基礎・基本』pp.108-109です．「平成元年に日米の数学的問題解決能力を比較するために，両国の小学校4年生に出題された問題」とのこと．なお，「かけ算」から始まる文は，独自に追加しました．
ななめになった長方形的配列のように見えますので，45度，回転させてみましょう．
残念ながら，長方形的な配列でない…と思いきや，4×4の配置と，3×3の配置が，重なっているように見えます．ということで，4×4＋3×3＝16＋9＝25によって，総数を求めることができました．
念のため1個ずつ順に数えても，あるいは2飛びでも，もしくは1＋3＋5＋7＋5＋3＋1＝（3＋7）＋（5×2）＋（1＋3＋1）＝10＋10＋5＝25としても，25個となることが確認できます．
「25＝5×5」*1に気づけば，もとのダイヤモンド的配列のおはじきを4つだけ，移動することで，正方形的配置になることが分かります．
ここまでの解法は，すべて，取り上げた書籍に書かれています*2．もう少し，考えてみます．
十字型に，切り分けてみましょう*3．上下左右の端を含む十字型を，4つ作ることができます．紙と鉛筆でなら，囲い込みをするところですが，PowerPointによる作図では，美しさに欠けるので，塗り分けることにします．
5つのおはじきからなる十字型が，4つ．残りは…塗りつぶしていない，白のおはじきも，ななめに見ると，十字型です*4．ということで，5つが5つで，5×5＝25を得ることができます．
塗り分けパターンがもう一つ，浮かびました．一つ分の大きさを「3」とします．L字型で，グルーピングをしていくわけです．
を経て，
とすると，3つが8つ，それと中心は，どのグループにも入っていないので足すことにして，3×8＋1＝24＋1＝25となりました．
*1:http://www.kasanken.com/03shidouan/2nen/2-20071006-kakezan.pdfに「アレイ図カルタ」というのがあります．「2×3と3×2は，カードの向きがちがうだけで，おなじなのにお手つきはおかしい」という児童の文句のほか，「余談になるが『5×5』のカードを探すときに，『まだもう一枚ある。』といって探していた子に，ほかの子が『1枚だけだよ。』と冷静に教えていたのがおもしろかった」が，目を引きます．アレイ図について，そのうちrepriseエントリを書きます．
*2:書籍に書かれていて，私が思いつかなかった考え方には，タマネギの皮を剥くように，ダイヤモンド型で外側から囲んでいくものがありました．それぞれの周の個数を数えて足し合わせれば，3×4＋2×4＋1×4＋1＝12＋8＋4＋1＝25を得ます．
*3:某日追記：この方法は，『算数好きにする教科書プラス 坪田算数2年生 (TEXT BOOK PLUS)』p.67に書かれていました．
*4:細かいことを言うと，おはじき間の距離は，他の十字型より倍長いのですが．
