わさっきhb

大学（教育研究）とか ，親馬鹿とか，和歌山とか，とか，とか．

2012年に「×」から学んだこと

5×3

目次

  • 問題を簡単に説明してくれますか?
  • 「かけ算の順序」への批判を，どのように考えていますか?
  • 「かけ算の順序」という言葉を使わずに，説明できますか?
    1. 無意味な問題も，意味のある問題もある
    2. 海外の順序，日本式の順序
    3. トランプ配りの適用
    4. 学校教育はその考え方を採用していない
    5. 数学ではなく数学教育
    6. 交換法則ではない
  • タダで，この問題を理解するには，何を見ればいいでしょうか?
  • 本を買いますので，この問題をもっと理解するには，どうしたらいいでしょうか?
  • 子どもが，学校で正しいとするかけ算の式で書いているか，チェックする方法って，ありますか?
  • トランプ配りで考える子が，いましたよね?
  • 「かけ算の順序」について書いた論文は，本当にないのですか?
  • あなたは，どんな子どもになってほしいと願うのですか? かけ算の式は一つ，ですか?

問題を簡単に説明してくれますか?


「さらが 5まい あります。1さらに りんごが 3こずつ のって います。りんごは ぜんぶで 何こ あるでしょう。」という文章題（《問い》）と，「しき」と「こたえ」を書く欄があります．
子どもは「しき」に「5×3＝15」，「こたえ」に「15こ」と書いたところ，「こたえ」はマル（正解）だけれど，「しき」のほうがバツ（不正解）で，そばに「3×5＝15」と赤で書かれました．
このようにバツとするのが適切なのかどうかが，議論の対象です．
ここで私のスタンスを書いておきます．私は，この出題でバツをつけることに賛成です．この1問を通して見える，それまでの授業，そして算数・数学教育に，共感を覚えます．これまでに読んできた書籍・論文や，Webの情報（とりわけ学習指導案）から，学んでもらいたいことの共通項を知ることができました．その知識やものの見方を，大学での研究教育，また子育てにも活用しています．
最近（ともに2011年12月），注目を集めた類題がありますので，リンクします．

「かけ算の順序」への批判を，どのように考えていますか?

できるだけ簡潔に，批判の分類と私の見解を書いてみます．

  • 順序づけることが無意味 → 無意味な問題も，意味のある問題もある．
  • 海外では逆 → 多くの関係者は知っている．そして日本式の良さを言う人もいる．
  • トランプ配りで考えれば，逆にできる → トランプ配りの適用が非現実的な場面がある．
  • アレイ図で考えれば，逆にできる → 学校教育はその考え方を採用していない．
  • 単位をつければいい → 学校教育はその考え方を採用していない．
  • 数学は自由であるべきだ → 数学そのものではなく，数学教育の課題．
  • 交換法則により5×3＝3×5 → 場面に対応するのは，その性質・等式ではない．

「かけ算の順序」という言葉を使わずに，説明できますか?

(1) 無意味な問題も，意味のある問題もある

[Greer 1992]では，かけ算が使われる場面を〈乗数と被乗数が区別される文脈〉と〈乗数と被乗数を区別しない文脈〉*1に大別し，それぞれの中で細かい分類を試みています．詳しくは2011年10月13日（Greerによる，乗法・除法が用いられる場合）をご覧ください．
《問い》は，〈乗数と被乗数が区別される文脈〉に該当します．そこに現れる，「5」と「3」という2つの数は，異なる役割を担っています．皿の枚数は「乗数（かける数）」であり，1皿に乗るりんごの数すなわち「被乗数（かけられる数）」に作用して，答えとなる総数が得られるのです．
〈乗数と被乗数を区別しない文脈〉として，デカルト積，長方形の面積，電力量などの物理量が記載されています．したがって，バツへの反論として見られる「面積を考えたら…」「アレイ図にしたら…」「物理学では…」といった種類の批判は，“かけ算は一つ”と言っているようなものです．そこには（2年のかけ算の導入にとどまらず，全学年を通じた）乗法の意味理解を促す活動に対して，配慮が不十分であるように思えます．
なお，かけ算で表される対象やその方略として，これまで《倍の乗法》《積の乗法》《倍指向》《積指向》と命名し，検討してきました．2011年11月15日（「倍」と「積」から学んだこと）をご覧ください．

(2) 海外の順序，日本式の順序

[Greer 1992]では，乗数と被乗数の区別をしたときに，「乗数×被乗数」と書くべきか，「被乗数×乗数」と書くべきかについては，論じていません．これらは，各国の言語や文化，そして教育内容によって（国ごとに）決まる，と考えるのが良さそうです．[馬場2002]pp.35-39に，「掛け算の語順」を含め，留意すべき点が記されています．
[銀林1975a]では，「乗数×被乗数」による表し方に“乗数先書”，「被乗数×乗数」には“被乗数先書”という名称をつけています．「a倍のb」や「a times b」は乗数先書であり，一方，「aのb倍」や「a multiplied by b」は被乗数先書と言えます．
このようにしたとき，確かに，日本では被乗数先書であり，海外では乗数先書です．これらの違いに注意し，日本の数学教育の成果や教材を，海外で活用してもらおうとするときに，配慮をしているいくつかの事例を，2011年11月9日（日本の「かけ算」，世界へ・世界と）にまとめています．
被乗数先書すなわち日本式のメリットが記されたものに，[中島1968b][森2009]*2[筑波2012]の3つがあります．前二者は，2012年2月24日（2aは「2つのa」）で紹介しています．[筑波2012]（磯田正美「我々は，何を，なぜ，いかに教えるか」pp.10-11）では下図のように，日本式とスペイン語での，三の段の違いを示しています．

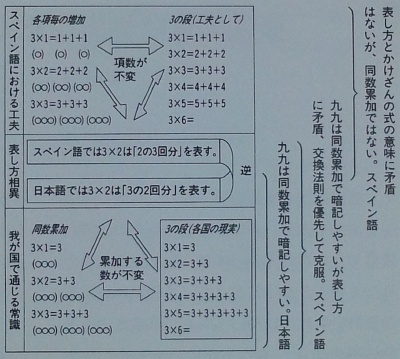
残念ながら，被乗数先書が良いとする海外文献は持っていません．かけ算から離れ年月日の表記については，ISO8601，RFC3339で日本式の「年，月，日」が採用されているとのことです（日付の順番がややこしい件 - エキサイトニュース(1/3)）．

(3) トランプ配りの適用

「トランプ配りって何?」という方は，まず2012年1月6日（トランプ配り）をどうぞ．
私の知る限り，トランプ配りの乗法への適用を最初に試みたのは，遠山啓です．科学朝日1972年5月号に記事があり，[遠山1978]pp.114-121で読むことができます．
現在では，トランプ配りは，等分除の説明で用いられます．日本ローカルではなく，[Greer 1992]にも載っています．
トランプ配りでかけ算を考えるのが非現実的な場面として，連続量×分離量になるタイプ，分離量×分離量になるタイプが考えられ，2011年12月26日（小学校の算数は解決を待っている魅力的な文章題でいっぱいだ）で列挙しています．以下，その中から1問を紹介します．
「ボートが ３そう あります。１そうに ２人ずつ のって います。ぜんぶで 何人 のって いますか。」は，東京書籍の教科書に載っている問題です．これに対して，ボートを3そう用意しておき，1人ずつ2回乗せていくという，トランプ配りに基づくと，「3×2＝6」とする余地はあります．しかし現実のボートで，そういう乗り方は，考えにくいですね．1人がボートに乗った状態で2人目を待つ，そんなボートが何そうもあるというのは，運営上，ずいぶん危険です．

(4) 学校教育はその考え方を採用していない

「問題の場面をアレイ図で捉えること」「式に単位をつけて，“5まい×3こ/まい＝15こ”のように解釈すること」は，学習指導要領解説や，Webで知る限りの教科書，また出題例と照らし合わせて，現場教育に相容れません．
まず，アレイ図は，「数学教育の現代化運動」に合わせて出現した，比較的新しいモデルです．現代化は昭和52年の学習指導要領改訂で，姿を消しています．
そういった政治的な話と別に，アレイに基づく乗法的構造の理解・モデル化には，2つの弱点を指摘できます．「倍概念」「量の感覚」「結合法則」の理解が困難であることと，一つの場面から2種類しか式が得られないことです．アレイ図の特徴や限界は，2012年1月25日（アレイ図）でまとめています．場面と式について，例を示します．

●●●●
●●●●
●●●●

上の図で，●の数を求める式を書きましょう，という質問をすれば，3×4＝12，4×3＝12が容易に思い浮かびます．しかし，アレイに基づくと，●を移動しない限り，そこでおしまいです．
「一つ分の大きさ×幾つ分」に基づくなら，“3個が1列で4列”，“4個が1行で3行”のほか，“2個ずつ6組”，“6個ずつ2グループ”といった取り方ができます．したがって，2×6＝12，6×2＝12という式もまた，正解に加えることができます．●を動かさなくても，そういった多様な考え方そして式が得られるのは，「一つ分の大きさ×幾つ分」で考えることの良さを示しています．
“5まい×3こ/まい＝15こ”のように，式に単位をつける方針を，学校教育に採用して欲しいという人は，数学的な土台すなわち量の理論と，その方針による小学校算数の一貫した指導方法について，構築・提案をお願いしたいと思います．
私は[銀林1975a][銀林1975b]を読み，複内包量・逆内包量といった興味深い量まで知ることができましたが，両書の中に，“5まい×3こ/まい＝15こ”あるいは“3km/(km/時)×4km/時”（[高橋2011]p.43）のような式や量の表記，そしてそれらを導出する理路を，見つけることができませんでした．

(5) 数学ではなく数学教育

「数学教育学」は，「数学」と別の学問として，確立しています．数学教育学を詳しく知りたい人は，[日数教2010]，[杉山2012]をどうぞ．
2つの違いを，いくつか挙げてみます．「数学の論文*3」と「数学教育学の論文」は，異なります．したがって「数学者が読む論文」と「数学教育学に携わる人々が読む文書」も，異なります．とうぜん，「数学者の語彙」と「数学教育学に携わる人々の語彙」も，異なります．
しかし最も大きな違いは，次のことだと思います．数学（という学問）では，論文を書く人と，それを読む人は，対等であることを前提とします．一方，数学教育においては，問題を作る人と，それを解く人は，対等ではありません．
算数・数学（という教科．入試を含みます）では，出題者が，解答者の能力や学習事項も考慮した上で，問題文を作成し提示することになります．
「解答者の能力」「学習事項」のバリエーションを意識し，どのように問題を提示してそこから解決・学習をさせるかについては，数学（という学問）の知見のみでは得られません．
そこではむしろ，教材研究・授業研究(jugyou kenkyuu，[スティグラー2002])に代表される教師の活動や，診断的評価・形成的評価・総括的評価を含む各種教育評価の手法が，重要な役割を担ってきたわけです．
そういったことを無視し，「数学では…」「数学者は…」という言い方を根拠として，バツにするのはおかしいと語るのは，適切でないと考えます．

(6) 交換法則ではない

《問い》を見て，

  • 「ひとつぶんの大きさ×いくつぶん＝ぜんたいの大きさ」のしきで，あらわすことができます．ひとつぶんの大きさは，「りんごが 3こずつ」の3です．いくつぶんは，「さらが 5まい」の5です．だから，3×5と書いて，九九で「さんご，じゅうご」だから，「3×5＝15」です．答えは15こです．

と答える（考える）子と，

  • こうかんほうそくをつかって，あらわすことができます．3×5も5×3もおなじです．しきは「5×3＝15」です．答えは15こです．

と答える（考える）子，どちらを育てたいでしょうか．
交換法則は，例えば「5×3」といったかけ算の（フレーズ型の）式が与えられたときに，これは「3×5」という式と等しいといった使い方をします*4．アレイ図から明らかという主張に対しては，(i)《問い》を（囲い込みのない）アレイ図と対応づけていいのか，(ii)囲い込みのないアレイ図からなぜ「5×3」や「3×5」といった式が得られるのか，を解決しないといけません．
場面からかけ算の式を得ようとするとき，交換法則は使えません．すでにある式に対して，適用するのならいいのですが，《問い》のように式が書かれていない，それどころか，かけ算の式で表せるかどうかから判断しないといけない状況では，活用のしようがないのです．
「式に表す活動」と「式を読み取る活動」の違い，そして「私（子ども）が式を読み取ること」と「あなた（先生，大人）が式を読み取ること」の違いには，配慮をしたいものです．

タダで，この問題を理解するには，何を見ればいいでしょうか?

目的を「かけ算の順序論争に決着をつけること」ではなく「乗法の意味理解についての知識を持つこと」とすれば，読んでおくといい情報はかなりあります．ここに整理してみます．

まず，現在の小学校で，算数指導の基準となる文書が

  • 小学校学習指導要領解説編 算数編（《算数解説》）

です．PDFファイルになっています．入手方法は2011年8月30日（学習指導要領を読む）にまとめています．小学校の算数は，平成21年度（2009年度）からこの内容に基づいています（先行実施; 移行期間あり）．
通し読みもいいのですが，文書内検索をして，用語がどこで出現するか，慣れ親しむことをおすすめします．「順序」「累加」「感覚」「をかける」あたりで，試してみてください．
次に，用語集をブックマークしましょう．分からない言葉を見かけたとき，立ち返りやすくなります．次のサイトと各ページには，よくお世話になっています．

では，「乗法の意味理解」に関する論文を読みましょう．

かけ算を主なテーマとしない文章題も，読んでおいて損はないと思います．

古い論文を読んでいると，「今の算数教育と，同じなのだろうか」という疑問が出てきます．学習指導要領は，だいたい10年のスパンで改訂されています．次のサイトから，読むことができます．

国際比較，外国の指導方法などについても，おすすめの情報があります．

ここで日本に戻ります．“何の何倍”すなわち倍概念に基づき，数学的に検討した「量の理論」があります．南雲道夫の論文は，和文・英文とも，無料です．

多くの出題例を知っておくと，出題と学習事項とのつながりが見えやすくなってきます．

本を買いますので，この問題をもっと理解するには，どうしたらいいでしょうか?

はい．何はなくとも，まず次の本でしょう．

この本については何度か取り上げていて，2011年12月19日（「かけ算の順序」のダブスタ考）で主要なものにリンクしています．「どっちでもいい」に基づく教育こそ，「1株61万円で売る株を，1円で61万株を売るという誤発注」（[高橋2011]p.iii）を引き起こしやすくなるように思えてなりません．
トランプ配り（カード式配り方）について書かれていて，比較的容易に手に入る本（と該当ページ）には，次の3冊があります．

遠山啓，矢野健太郎，森毅のいずれも，日本の数学そして数学教育を代表する者であると言っていいでしょう．数学教育協議会会員（物故者でもありますが）という共通点もあります．
そういったカリスマだけが，算数教育を，かけ算のことを，論じていたわけではありません．学会や研究会は，会誌に載った論文・論説を整理して，新たに出版しています．「乗法の意味」が整理されている本を，日本数学教育学会と新算数教育研究会から，1冊ずつ挙げます．

現場の先生方の考え方や取り組みについて，おすすめの本をいくつか並べます．

「どちらでもいい」とする本も，あります．

数学と数学教育の関わりについて，次の2冊に感銘を受けました．

そろそろ，用語集も必要になってきます．次の辞典は，学習指導要領改訂のたびに改訂されています．

論文に移ります．CiNiiで見つかる文献には，有料ダウンロードできるものがあります．次の2つは，乗法の意味理解に関する論文として，何はなくともです．

古いだけでなく，[中島1968b]にある「わが国の立場」は，[日数教2010]の「乗法・除法の意味づけ」(pp.73-75)の結論と同一である点も，無視するわけにいきません．
[中島1968a]は，タイトルからは分かりにくいのですが，乗法の意味の拡張に関する意識調査です．これを踏まえ，実施時期の状況に合わせた実態調査の論文が複数あります．有料ダウンロードできる一つを，書いておきます．

電子配布されていない論文の中で，乗法の意味を小学生と大学生に問い，比較しているものがあります．

洋書における「乗法の意味理解」のうち，次の2つは，日本の数学教育の論文・解説書でよく，参考文献に挙げられています．出題例・式の解釈が豊富です．

「量の理論」に関する，数学者が著した本には，大きく2つの系統があります．一つは倍概念に基づくもので，高木貞治，田村二郎，小島順の名前を挙げることができます．2012年2月13日（数学者による「かけ算の順序」）からご覧ください．
もう一つの「量の理論」は，“内包量×外延量”に象徴される，数学教育協議会ベースのものです．銀林浩による2冊の本から読み始めるといいでしょう．

あとは，最新刊の本や雑誌を読んで，著者の主張が，これまで書かれたうちのどこに位置づけられるかを見ていくのがいいでしょう．まさにいま最新の1冊を，書いておきます．

子どもが，学校で正しいとするかけ算の式で書いているか，チェックする方法って，ありますか?

チェックをしたいという気持ちは分かりますが，お願いが2つあります．一つは，正誤判定，すなわちマルかバツかだけにとらわれないことをお願いします．間違いなら，どうすれば正解になるかを，話し合ってください．正解ばかりのときにも，その中から1問「どうして?」と聞いてみると，相互理解が深まり，うまくやればお子さんに自信をつけることができます．
もう一つは，〈乗数と被乗数を区別しない文脈〉が2年の学習内容にも含まれていることへの理解です．その種の問題ではおそらく，かけられる数とかける数を交換した式も，正解となります．お子さんよりのいないところで，問題集と解答を通し読みしておけば，そのことに気づきやすくなります．これもまた，配慮だと思います．
とはいえ，いろいろ読む中で知ったり，自分も作ったりした中で，良さそうな問題を挙げていきます．
一つは，連続量×分離量のタイプです．1問，示します．

  • ひもを4等分した一つ分を測ったら9cmあった．はじめのひもの長さは何cmか．

これは《算数解説》で，第3学年の中に記載されています．乗法と除法の関係（「等分」と書いてあるからといって，わり算ではないこと）を確認するための出題です．しかし2年でも，場面を適切にイメージして，かけられる数とかける数が何になるかを判断し，式で表すことができます．
このように，何問かの文章題の中に，かける数がかけられる数よりも先に出現し，かつかけられる数が連続量（cm，秒，mlなど），かける数が分離量（回，枚，人など）となるような問題を入れてみてはいかがでしょうか．
次は，反比例に基づく出題が考えられます．

  • いつも3人で手分けして，庭の水やりをします．11時30分に始め，11時42分に終わります．ある日，あなたひとりだけで，庭の水やりをすることになりました．12時ちょうどのお昼ごはんに，間に合うでしょうか．

これは自作したもので，初出は2012年1月27日（4マス関係表）です．
立式・計算なら，2年でもできます．学年が上がり，水やりという仕事への理解や，時間を用いた量の感覚が不十分な子どもだと，12÷3＝4とやってしまうかもしれませんよ．
最後は，5〜6年になりますが，全国学力テストに，かけ算かわり算かを判定（演算決定）させる出題があります．

答えが210×0.6の式で求められる問題を，下の1から4までの中から1つ選んで，その番号を書きましょう。

  1. 砂糖を0.6kg買って，210円はらいました。この砂糖1kgのねだんはいくらでしょう。
  2. 210kgの大豆を0.6kgずつふくろにつめます。大豆を全部つめるには，ふくろはいくついるでしょう。
  3. 1mのねだんが210円のリボンを0.6m買いました。リボンの代金はいくらでしょう。
  4. 赤いテープの長さは210cmです。赤いテープの長さは白いテープの長さの0.6倍です。白いテープの長さは何cmでしょう。

（平成19年度 全国学力・学習状況調査 小学校算数A 大問4）

「掛け合い」でテンポ良く答えられるようにしたければ，"99qg"の利用をご検討ください（2011年8月24日（九九文章題ジェネレータ“99qg”をリリース））．

トランプ配りで考える子が，いましたよね?

2011年12月22日（大人の私たちの考えは，教育現場に届かない）に書いた，発言小町の件の件ですね．
荒療治とも言える対策は，これまで書いてきましたが（2011年12月26日（小学校の算数は解決を待っている魅力的な文章題でいっぱいだ），2012年1月4日（なぜ教材研究）Ｑ３），別の観点から，「トランプ配りで考える子」への疑問点を，示しておくことにします．
それは，「トランプ配りで考える子」の存在を，学術評価に耐える形で確認できておらず，それどころか，適切な方法で確認することが困難なのではないかということです．
発言小町でトピ主さんが書かれた“確認方法”では，会話中や，会話後（レスとして書くまでの間）の，トピ主さんのバイアスが無視できません．
バイアスを取り除いて「確かに，トランプ配りで考えている」と示すのには，数学教育学にこだわる必要はないとしても，量的研究または質的研究の手法が不可欠と言えるでしょう．
とはいえ私は，「トランプ配りで考える子の存在」にあまり関心を持てませんし，数学教育に関わる大部分の現職教師や研究者も，論文や記事などを読む限り，トランプ配りに関心を持たれていないようなので，その存在を実証し，論文として公表するのは，それをしたいという強い意欲のある人に，お任せとなります．
「適切な方法で確認することが困難」というのは，現在の学校教育で，乗法の意味理解にトランプ配りを取り入れていない点から，検討を始める必要があるでしょう．
その検討の結論は，例えばこうなります．《問い》の「しき」に「5×3＝15」を書き，どうしてかと聞かれてトランプ配りを行う子は，親や教師にとって「それは，お兄ちゃんかお姉ちゃんか，それともインターネットで，知ったのかな」という反応に至る可能性が高く，「自分でよくそこまで考えたね」とはならないように思えるのです．
「確認する」ことは，適切にセッティングすれば，おそらくは可能でしょう．しかし“トランプ配りモデル”が本当に，授業や日常生活の経験を経て，自分の中で作られたイメージであるかを判断するのは，容易ではないということです．日常生活を2年生の子（それと親）に根掘り葉掘り聞くのでいいのですか，と付記することにします．

「かけ算の順序」について書いた論文は，本当にないのですか?

「かけ算の順序」のことが書かれている，学術文献は，把握している限り2つあります．
一つめ．

この中には，「式の順序とかけ算の意味との対応づけ」「かけ算の意味と式の順序との対応づけ」「『一あたり量×いくつ分』という順序」といった形で“順序”が使われています．
もう一つ．

こちらは，引用しましょう．

そこで問題となるのは、例えばタイでは自然な語順が日本語式であるにもかかわらず、教科書は英語式の順番に従っている。単にかけ算の順序が逆になっただけで小さなことのようであるが、初めての学習者にとってはかなりの認知的な負担が強いられるだろう。
(p.38．強調は引用者)

それぞれ読めば分かるように，順序がどうあるべきだという議論ではありません．日本では被乗数先書，これを前提としています．その上で，子どもに定着させるにはどうするか，海外向け教材開発はどうすればいいのかについて，それぞれページをとっています．

あなたは，どんな子どもになってほしいと願うのですか? かけ算の式は一つ，ですか?

上に書いた，縦に3つ，横に4つのアレイの事例から，「かけ算の式は一つ」ではないことは，ご確認いただけると思います．
ふだんの研究・教育活動から得た問題意識は，1文に凝縮できます．

  • 「一つの問題に対して，複数の解決法があるとき，どれを選んで，形にするか?」（2011年2月14日（自分を支えるものは何か，考えてみた））

工学の要素を取り除いて我が子に教え，自らも行動し苦悩し，子らに引き継いでもらうことを，今のところ，人生をかけた目的の一つとしています．
（最終更新日時：Tue Mar 20 06:15:46 2012ごろ．文献ラベルの[銀林1975a]を[銀林1975b]に変更しました．）

*1:これらのラベリングは，[小原2007]によります．

*2:初出は「科学朝日」の1977年．

*3:2011年2月4日（論文を読もう，引用しよう）に書いたうち「広義の論文」を指します．以降の「論文」も同様です．

*4:5×3＝3×5を（例えば代数的に）確かめるには，5×3＝15，3×5＝15として，これでいいじゃないかと言いたくなりますが，不十分です．等号が同値関係であることを用いてやっと，5×3＝3×5と書けます．このとき，同値関係の諸性質，具体的には反射性・対称性・推移性を，いつ学習すればいいのかという問題も出てきます．

*5:Thanks: http://ameblo.jp/metameta7/entry-11130552407.html