「かけ算の順序論争」も今は昔,なんて思いつつ,本を読んでみると,まだまだ気になることが出てきました.本日もその一つを書いていくのですが,中期的には,「論点」「対立」の洗い出しというのを,していけばいいのかなと考えています.
一例を挙げておきます.
この出題で期待されているのは,つばさが6×2,あおいが2×6ということなのでしょう.
本から学んだ「かけ算の順序」ツアー
そして,まとめとして引き出したいのは,“かけ算の式で表すときは,問題文から「1つ分の大きさ」と「いくつ分」を見つけるようにする”だと思います.
これを見たとき,こういう反論もできそうです.“このように,ペアで与えられた場合には,書き分けるのに賛成するが,このうち一方しか出題されなかったら,交換法則やトランプ配りを使って,どちらのかけ算の式でもよい”です.
この種の対立は,「かけ算の順序論争」のいろいろなシーンで,見ることができます.そこはどちらが教育的であるか,学習者である子どもたちに配慮されているか,でもって,先生方そして学校が選択していただくしかないのかな,と思っています.
一般化すると,こうです.ある問題(issue)に対して,Xという考え方とYという考え方があり,どうやら学校教育ではXを採っているのに対し,「かけ算の順序」を旗印に言動をしている人々は,Yを採っている,そんなXとYのペアを見つけていこう,というものです.
といったところで,新たに読んだ本を.

読み取り表す力を育てる「足場」のある算数授業―すぐに使える!読解問題付き
- 作者: 石田淳一
- 出版社/メーカー: 明治図書出版
- 発売日: 2011/02
- メディア: 単行本
- この商品を含むブログを見る
2学年で学習するかけ算から,抜き出します.
ベンチが4つあります。1つのベンチに子どもが3人ずつ座りました。まだ,5人立っています.子どもは全部で何人いるでしょう。
T この問題を図でかいてみましょう。
T 図Aと図Bのどちらが,この問題に合っていますか。
C 図Bは,4人ずつになっているから違う。
C 図Aは,3人ずつだし,ベンチも4つある。
T 図を見て,どんな式になるのか説明しましょう。
C 3人ずつのまとまりが4つあるので,3×4です。まだ,5人残っているので,それをたします。
(p.29)
○問題文では基準量が後に示されているので,図をかくことによって,3が基準量であり,4がいくつ分であることを理解させる。
(同)
この授業事例では,「基準量×いくつ分=全体の量」(p.28)という書き方を採用しています.「基準量」という言葉は,あまりなじみでない…と思いきや,すでに少なからぬ数を書き出していました.
ただ,今回取り上げた出題は,《BA型》あるいは《乗》に,「まだ,5人立っています」という,たし算が入っています.《AB型》あるいは《被》に,たし算を入れた問題,ひき算を入れた問題も見られます.
一つの問題に対して,かけ算を使って複数の方法で異なる式を立て,共通する答えを求めるのは,pp.32-33にも見られます.ですが,ああこういうのこそきちんと,当雑記で取り上げないとと思ったのは,p.108にあります.6学年で,「比を使って問題を解こう」という授業事例です.
「さとうと小麦粉の重さの比を2:5にしてケーキをつくります」という前提を置き,いくつか問題を解きます.本エントリでは「小麦粉を150gにすると、さとうは何gいりますか」という問題1に着目します.
男の子(たくやさん)は「比の1にあたる量を求めます」という方針をとっています.帰一法ですね.150÷5=30で,比の1にあたる量は30gです.さとうは比の2にあたる量なので,30×2=60とし,答えは60gです.
女の子(えつこさん)は,2:5=□:150という,比の形の等式を利用します.コロンのあとの5と150から,「×30」という関係を得ます.2と□にも,「×30」の関係がある(「等しい比の性質」)ので,2×30=60とし,答えは60gです.
式だけを見ると,「30×2=60」と「2×30=60」のいずれも,この問題を解くのに使用してよい式と言えます.なお,一つの場面に対して,かけられる数とかける数を交換した2つのかけ算の式がともに正答とできる事例を,第2用法で書いていますが,単位のつけ方と,後で述べる「数量関係」に着目すると,今回はそれとは異なる事例と言えます.
さてこの2人の考え方は,表を作って関係を添えると,違いが明確になります.男の子(たくやさん)のプロセスは,次の表になります.
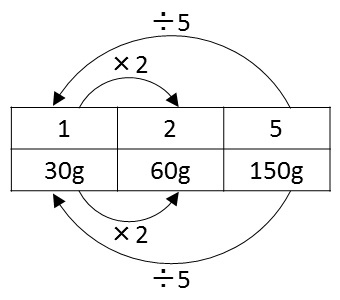
4マスではなく6マスですが,「1と5の列」と「1と2の列」の2つの4マスをくっつけた次第です.
女の子(えつこさん)の表は,次のとおり.
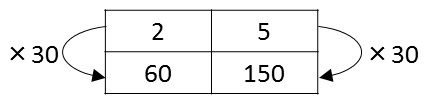
「2」と「5」は無次元量で同じ種類の数なので,上の行に書き,「60」と「150」は重さでこれまた同じ種類とできるので下の行に置きます.
黒板の「小麦粉の比に×30をすると150になります」は,5と150という上下を見たときの関係を言っているわけです.このように,2つの異なる種類の数を「×数」と結びつけることは,[Vergnaud 1983]のp.130,『算数・数学科重要用語300の基礎知識』p.187,『田中博史の算数授業のつくり方』p.146でも見ることができます.
なお,上述のとおり「5」は無次元量ですが,「150」にはgという単位が付きます.ということは,「×30」は「×30g」にすべきではないか,と考えることもできます.すると,5×30g=150g(あるいは150g÷5=30g),そして2×30g=60gとなります.
Vergnaudほかから学んだところでは,2つの異なる種類の“量”を「×数[次元]」と結びつけることで,「a[d1]×b[d2/d1]=p[d2]」という式を得ることもできます.これは「いくら分×1あたり量=全体量」の形であり,学校で学んでいる式と,かけられる数・かける数が反対になっています.
その式は,次のように解釈できます.「×b[d2/d1]」が,a[d1]とp[d2]の間の乗法的関係を結びつける関数作用素であり,bの次元はaとpbのそれらをもとに(次元解析によって)定まる,ということです.このときbは,数教協スタイルで2年から学習している「1あたり量」というよりは,「単位あたり量」となります.「1あたり量」は,乗法の構成要素(積を求めるための因数の一つ)として導入されるのに対し,「単位あたり量」は,既知の2つの量の商によって算出する,という違いがあります.なお,学習指導要領では「単位量当たりの大きさ」と表記されています.
別のアプローチとして,単位を取り除き,先ほどのえつこさんの表のように,同じ列の上下の値の関係を式にすると,□=△×30(上の数を30倍したら下の数になる)と表せます.このように,2つの数量の関係を式で表すことは,学習指導要領でも第4学年と第5学年で記載されています.4つの領域(数と計算,量と測定,図形,数量関係)のうち「数量関係」に属します.
さて,上下の値の関係は,□=30×△という式で書くこともできます.△と□に値を代入することで確認できますし,直感的には,乗法の交換法則が成り立つことを根拠とするのでもいいでしょう.そして絶妙なことに,交換法則を他の法則とともに整理するのもまた,第4学年の数量関係のところです*2.
他の本からも学んだことを加え,さしあたりの結論を書いておきたいと思います.小学校の算数の出題において,「かけられる数とかける数を反対に書いてもよい(バツとされない)」のは,交換法則や,それに限らない数量の関係を○,△,□などで表すようになる時点,学年で言うと4年あたりからではないかということです.
まったくどうでもいい話ですが,男の子と女の子の人名のうち一方は,pp.108-109記載のものから変更しています.
(最終更新日時:Wed Jun 6 06:14:43 2012ごろ)

