wikipedia:かけ算の順序問題が,11月3日にずいぶんと充実しました.その後,差し戻し,そのまた差し戻しとあって,定着しない段階の編集はこんなことになるのかと,外の者ですが驚きを隠せません.
ともあれ今後,オンライン百科事典の1項目として整備していくにあたり,最も厄介そうな問題は,何度も使用されている「かけ算の順序」という言葉の,発生経緯と普及度です.
個人的に把握しているのは次のとおり.*1
- 『新式算術講義 (ちくま学芸文庫)』p.31に「加法及乗法は(略)其順序を如何様に変更するとも結果は常に同一なり」とあります.
- 遠山啓「6×4,4×6論争にひそむ意味」には,「順序」が見られません.
- http://www.math.tohoku.ac.jp/~kuroki/keijiban/a0018.html#a19980821195612は,個人的に知り得る,インターネット上で最古の「掛け算の順序」です.「掛け算に順番はあるのですか?」がSubjectを含め2度出たあとで,最後の文に「掛け算の順序」とあるのも,目を引きます.
- 出題例とその解説,授業例を見る限り,論争の意味での「かけ算の順序(順番)」を,小学校では使用していない模様です.例えば,http://www.shinko-keirin.co.jp/keirinkan/sansu/jissen/1003/2nen/index.htmでは「かけ算を使う場面把握・被乗数と乗数の理解」が要所と言えます.ページ中に,以前に《BA型》《複数解》とラベリングした出題も,見ることができますが,そこでも順序・順番という言葉は出てきません.
- 『算数授業研究 VOL.80』に見られる「順序性」などは,『かけ算には順序があるのか』に影響されたものでしょう.
- 「かけ算の意味理解を促すための問題状況の図示の試み」には,論争と対応する「式の順序」「正しい順序」が何度も現れます.これらの言葉が何によって入り込んだのかは,謎です.藤野(1985)の文献も,本文の言及を見ると,そこに「順序」が書かれていないのが推測できます.
「かけ算の順序」という言葉を使用することの課題は,既存の,算数・数学教育における「順序」の使用と衝突するところにあります.
まずは,学習指導要領解説に書かれている「計算の順序」です.
第4学年では,数量の関係を式に表したり,式を読み取ったりする力を伸ばすとともに,計算の順序についてのきまりなどを理解し,適切に式を用いることができるようにすること,さらに,既習の式と,具体的な場面での立式などを基に,公式についての考え方を身に付けさせることをねらいとしている。
(p.157)
「計算の順序についてのきまり」については,直後(次のページ)で示されています.手短に言うなら,「カッコ優先」「乗除先行」です.
ア 四則の混合した式や( )を用いた式
第4学年では,単に式の計算に慣れさせるだけでなく,数量の関係を四則の混合した式や,( )を用いた式に表したり,そのような式を読み取ったりして,式のよさが分かるようにするとともに,式を適切に用いることができるようにすることをねらいとしている。
四則の混合した式や( )を用いた式は,前学年までにも指導してきているが,一つの数量を表すのに( )を用いることや乗法,除法を用いて表された式が一つの数量を表したりすることを確実に理解できるようにすることが主なねらいである。このことについて,いろいろな場面や問題で式に表したり,式から場面や一般的な関係を読み取ったりすることを通して,理解できるようにしていく。
指導に際して,乗法,除法を加法,減法より先に計算すること,( )の中を先に計算することなどのきまりがあることを理解できるようにし,習熟を図る。さらに,四則を混合させたり( )を用いたりして一つの式に表すことには,数量の関係を簡潔に表すことができるなどのよさがあることが分かるようにし,四則を混合させたり( )を用いたりして一つの式に表すことができるようにすることが大切である。
(p.158)
これと別の種類の,「計算」の「順序」もあります.それは交換法則と結合法則に関するものです.学習指導要領解説では,第2学年に入っています.
ウ 加法,減法について成り立つ性質
幾つかの数をまとめたり,順序を変えて計算したりする場合がある。例えば,25+19+1の計算をするとき,計算を能率的にするために25+(19+1)と考えることがある。また,16+8の結果と8+16の結果とを比べることで,計算の確かめをすることができる。このようなことを通して次第に計算に関して成り立つ性質に着目できるようにする。
ここで扱う性質としては,第2学年の「内容の取扱い」の(3)で「ウについては,交換法則や結合法則を取り扱うものとする」と示しているように,加法に関して成り立つ交換法則や結合法則を指導する。(略)
(p.85)
なお,乗法の結合法則に関する説明の初出は,第3学年のp.108で,学習指導要領の記述をなぞったにすぎず,式の例も見当たりません.
ここで,「計算の順序とは何なのか」から脱却してみます.交換法則と結合法則を合わせて,「計算の順序」に関する性質であると,設定することにします.
複素数の範囲までで,加法と乗法はそれぞれ,計算の順序を変えても答え(和,積)は同じになり,減法と除法では変わる(ので計算の順序を変えられない),となります.なお,a÷b÷c=a÷c÷bという等式もまた,「計算の順序を変えても結果は同じ」と言われることもあるので,注意したいところです.
このように設定した「計算の順序」と,合致する例はいくつかあります.まず冒頭に書いた,『新式算術講義』の話は,まさにこの意味の「順序」です.pp.33-34では,3つの数に対する「十二様の順序」を列挙しています.
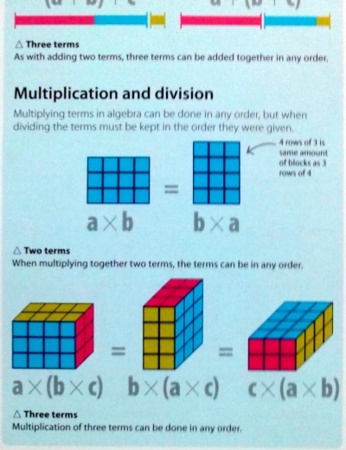
次に,『Help Your Kids With Maths』に書かれている,"multiplying terms"の"order"を見ます.
"Multiplying terms in algebra can be done in any order"を訳すと,「代数において,かけ算はどのような順序で計算してもよい」でしょうか.そして2つの項(因数),3つの項のかけ算の例は,和訳本と同じ図・式です.
ただしキャプションは違っていて,英語は「△Two terms」「△Three terms」,『親子で学ぶ数学図鑑:基礎からわかるビジュアルガイド』では「△乗法の交換法則」「△乗法の結合法則」です.前後のページも見ましたが,原文(英語版)には「交換法則」「結合法則」に対応する表現が見当たらりません.なので和訳の段階で,盛り込まれたようです.
3番目の例です.
今手元に教科書がないのですが、例えば
http://d.hatena.ne.jp/filinion/20101118/1290094089#c1350698256
「1個57円のおかしが、1箱に5こずつ入っています。これを2箱買うと、代金はいくらですか」
のような問題においては、「5×2=10」先に計算しても(おかしの数を先に求めても)よい、というのが確か教科書の立場でしたし、私もそう思います。
ここでは、式から1個あたりの値段を知ることはできません。
この引用より前に,同じ方(ブログ主さん)がコメントとして書かれている内容は,「a×bかb×aの一方か,それとも,どちらでもよいか」で,交換法則が関係する話です.しかし上記は,もっぱら結合法則に関する事例です.なぜこれが出てきたのかというと,交換法則と結合法則を合わせて一つの概念,つまるところそれを「計算の順序」として意識されていたからだと,推測できます.
これだけ事例があるのだから,交換法則と結合法則を合わせて「計算の順序」と言うのは十分定着しており,とりわけ加法・乗法についてはその順序を変えてもよいと考えてよいのかというと,実は判断を保留したいのです.
理由は2つあって,一つは,数学の観点です.交換法則と結合法則は,違う性質なのです.
周知の通り,行列の積は,交換法則が一般に成立せず結合法則のほうは成り立ちます.情報処理の分野で,行列を用いた座標変換(wikipedia:アフィン写像)に応用されます.http://www.hcn.zaq.ne.jp/___/SVG11-2nd/coords.html#NestedTransformationsが典型的でしょう.2つの変換行列を交換すると結果が変わり得る(交換法則は成立しない)のに対し,行列を順に左からかけていくのではなく,合成した行列を作ってそれをかけても,同じことを意味するというのは,結合法則があってこそです.
スカラーの場合と,比較をしておきます.y=x×3×2ならば,y=x×2×3です.ですがxやyをベクトル,2や3を適切な行列へと拡張したとき,同様の“ならば”関係は,必ずしも成り立ちません*2.なお「行列を左からかける」のは慣習であり,列ベクトルを転置させて行ベクトルとし,行列も転置させれば,その行列を右からかけることで,同じ結果になります.
交換法則が成り立たない数としては,他に「四元数」も押さえておきたいところです.複素数の拡張であることは,wikipedia:四元数のはじめに記されています.算数教育の観点でも,「形式不易の原理」に関連して,『算数教育指導用語辞典』p.19で取り上げられています.ここで数学から離れまして…
理由の2番目は,小学校の授業例です.乗法の結合法則を取り扱う中で,交換法則に関係する考え方を排除している例を,見かけるのです*3.
書籍からだと,『小学校算数 板書とノートを変えると子どもが伸びる』p.50が該当します.授業で「1こ60円のおかしが1はこに4つ入っています。このはこを2つ買うと,代金はいくらですか」という問題を提示し,目指すのは「(60×4)×2=60×(4×2)」です.その一方で,「4×2×60は問題場面に合わない」としています.
Webで読めるものだと,第3学年 算数科学習指導案(平成18年10月24日,調布市立杉森小学校)も同様の構成です.「1こ90円のシュークリームが、1はこに3こずつ入っています。2はこ買うと、代金は何円になるでしょう?」から90×(3×2)=(90×3)×2を導き,「かけ算はかける順番がかわっても、答えは変わらない」とまとめています.途中,「90×2=180 180×3=540」も,予想される児童の反応に入っていますが,これに対しては「机間指導する」となっていて,間違いとみなしています.
これらを見たあとで,filinionさんの持ち出された例題を確認すると,先に1箱あたりの値段を算出する「57×5」においては,「1箱に5こずつ」の5がかける数になり,先におかしの個数を求める「5×2」において5はかけられる数になります.2つのかけ算の式を見比べれば明らかですが,それぞれのかけ算の,5のもう一方の数が,異なっています.
結局のところここが,交換法則と結合法則の共通点そして相違点を表しているように思います.
いいまとめが思い浮かびません.「かけ算の順序」を批判する方々が,ここまで読んでいただいて,どうかどうか,算数教育における,かけ算を含めた「順序」の多彩な使われ方に,目を向けてくれないものかなあと,願ってもおそらく無駄でしょうしね.
(最終更新日時:Sun Nov 11 18:44:02 2012ごろ.「四元数」のことを追加しました)
*1:関連:かけ算の順序の伝統, かけ算にまつわる順序, 2012年に「×」から学んだこと(「かけ算の順序」について書いた論文は,本当にないのですか?)
*2:例えば,対角行列に制限すれば,行列どうしの積の交換法則も言えるのですが.
*3:「排除したいから」ではなく,2年で学習した「かけ算の意味」を,この場面でも---数が九九の範囲を超えるとともに,答えを得るために使う数が3つになっても---活用できることが,意図に入っているのでしょう.