累加・比例・面積〜ぼくのかんがえた Multiplicative Structures 2012

	離散的	連続的
区別あり	累加	倍
区別注意	1あたり	比例
区別なし	直積	面積

解き方

「さらが 5まいあります。1さらにりんごが 3こずつのっています。りんごはぜんぶで何こあるでしょう。」という問題に対して，

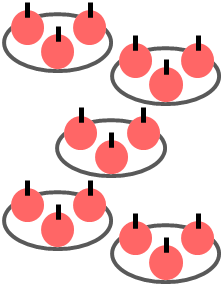
「累加」では，次の図を使って，3＋3＋3＋3＋3＝15と計算します．この左辺を「3×5」と書きます．

「倍」では，上の図を使って，“3”をかけられる数，“5”をかける数と認識し，3×5と式にして，3×5＝15と計算します．
「1あたり」では，上の図を使って，“3こ/さら”を1あたりの数，“5さら”をいくつ分と認識して，3こ/さら×5さら（または3×5）と式にし，3こ/さら×5さら＝15こ（または3×5＝15）と計算します．
「比例」では，次の図を使って，“3”を比例定数（または単位量当たりの大きさ），“5”をいくつ分と認識して，3×5と式にし，3×5＝15と計算します．

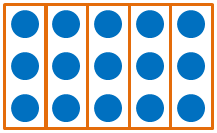
「直積」では，次の図を使って，3×5＝15（または5×3＝15）と計算します．

・・・・・
・・・・・
・・・・・

「面積」では，次の図を使って，3×5＝15（または5×3＝15）と計算します．

いくつか注意

2つの数の積によるかけ算を，対象としています．結合法則（□×（△×○）＝（□×△）×○），体積*1，複比例*2は今回，対象外となります．
「区別」とは，かけられる数・かける数の区別です．a×bで表される場面において，b×aと書くと，意味が変わるのが「区別あり」と「区別注意」，a×bでもb×aでもよいのが「区別なし」です．
「離散的」「連続的」はそれぞれ「分離量」「連続量」と読み替えてもかまいません．これらの用語の注意点は，分離量と連続量，かけ算とわり算のはじめのところをご覧ください．
「離散的」の対象は，a×bという式で表す際の「片方」を指す場合と「両方」を指す場合があります．具体的には，累加については，かける数(b)のみ離散的であることを要請し，かけられる数(a)は小数や分数であってもかまいません．1あたりと直積については，aもbも離散的なのを前提とします．
「倍概念」は「倍」と同義です．
「倍」と「比例」はそれぞれ，離散的な場面でも利用可能です．分類の都合上，連続的と位置づけました．
乗数を先に書く海外のスタイルだと，倍は「5×3＝15」になります．累加も少し修正が必要で，5×3＝3＋3＋3＋3＋3＝15（日本では，3×5＝3＋3＋3＋3＋3＝15）です．Vergnaudの考え方に基づくと，比例については上記から変更なしです．もちろん，直積や面積もそのままです．1あたりについては，海外でそのような解き方を見かけませんでした．

「区別注意」とは

1あたりと比例は，通常「1あたりの数×いくつ分」「y＝k×x（kは比例定数）」という式で表されます．かけられる数とかける数には，明確な区別があります．
なのですが，1あたりの数や比例定数に相当するものを，かける数として扱っている事例もあります．

「パーティー会場で4人用のテーブルがすべて満席となり、さらに7人がまだ座っていないことを想定しよう。このとき参加者の人数を数えるとき、どのようにするだろうか。恐らくテーブルの数を数えて、それに4を掛けて、その結果に7を足すだろう」（『いかにして問題をとくか・実践活用編』p.151；テーブルの数に4をかけるより孫引き）
Vergnaudの解説*3に見られる「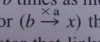」．なお，『算数・数学科重要用語300の基礎知識』p.187にも同じ表記があります．

それらは，比例関係にある2種類の数量において，下図*4のとおり，同じ列にある2つの数量の関係を，かけ算で表したものと言えます．

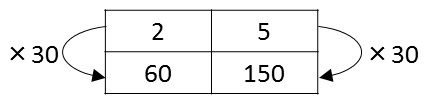
この関係において，かけられる数（基準量）は，表の上側にある数，かける数は矢印に添えた数（比例定数），そして積は表の下側の数です．これにより基準量×比例定数＝積という等式が得られます．これは「y＝x×k」と言っているようなもので，したがって逆にできるという次第です．
このように逆にできるのは，小学校の算数では「数量の関係を表す式」として，4年や5年で学習する内容をもとに，説明ができます．もちろん直接的に，交換法則を使えば，「いくつ分×1あたりの数」「y＝x×k」とでき，上の解き方で「5さら×3こ/さら＝15こ」という式に至るのですが，学校教育はその立場をとっていません．
ここまで書いた考え方と，いわゆるトランプ配り（例えば森毅『数の現象学 (ちくま学芸文庫)』pp.67-68；wikipedia:かけ算の順序問題にも記載あり）や，『かけ算には順序があるのか (岩波科学ライブラリー)』p.43の「3km/(km/時)×4km/時」に象徴されるロジックとの，関連性については，検討の価値があるようにも思います．

ヒートマップ

「小学校ではどのようにかけ算への理解を深めていくのか」「校外からはどのように見ればいいのか」といった問題意識で，乗法の意味の理解のあり方を考えてみます．
これですが，3行2列（表側・表頭を除く）でエントリ冒頭に示した表について，それぞれのセルにその重要度に応じて背景色を塗り，いわばヒートマップとして，視覚化するのがよさそうです．
小学校で，2年のかけ算の単元終了時には，こうでしょうか．直積に色がついているのは，「アレイ」があるからです．

5年で，小数のかけ算を学習する時点では，こうなります．累加の色がそこそこあるのは，児童らは小数をかける場合でも累加で考える傾向があるのと，分数×整数でまだ使うからです．

比例や，順列・組み合わせまで学習を終え，小学校卒業時には，次の状態を期待したいところ．

「1あたりの数×いくつ分」を活用する，数教協スタイル*8では，話が変わってきます．2年終了時の状態のみ，載せておきます．

最後に，「かけ算の順序」の批判者は，こんな感じでしょうか．

そこでの“熱さ”は2年学習時のものと明らかに異なっており，これが，教育とネットとの違いを表しているわけです．

まとめ

乗法（かけ算）の意味づけは，書籍からでもネットの議論でも，多岐にわたります．今回，「累加」「倍」「1あたり」「比例」「直積」「面積」という6項目を表に入れ，分類を試みました．項目間の関係や，学校内外の人々の認識の度合いを表すのに，活用いただければ幸いです．
そうだそうだ…私自身のヒートマップはと言いますと，場面によって強弱が変わります．どのマスも，最大から最小まで変わり得ます．なのでもし，画像化するなら，アニメーションGIFにしたいところです．