わさっきhb

大学（教育研究）とか ，親馬鹿とか，和歌山とか，とか，とか．

1973年は積集合の構造，2010年は乗法的構造

OoM

1. 1973年―森・竹内

数学の世界―それは現代人に何を意味するか (中公新書 317)

数学の世界―それは現代人に何を意味するか (中公新書 317)

昭和48年3月25日発行の新書版です．ISBNはついていませんが，Amazonの情報には，入っています．
帯によると森は京大教授，竹内は東大助教授．この2人の対談形式で，話は進んでいきます．
かけ算についてのやりとりは，「◎ 2×5と5×2は区別しなければいけないか」(p.70)から始まります．この小見出しに対する直接的な答えを，得ることはできませんが，竹内の「5本×2でも2×5本でも、それは単なる習慣なのだからどちらでもかまわないではないか」(p.75)，森の「本来，2×5か5×2という問題は、正比例の構造を理解することにあるんです」が，おもな主張となっています．*1．
対話の中に2ページ，囲み記事になっているところがあります(pp.71-72)．「乗除」と題してあり，末尾の「(M)」から，森が書いたものと思われます．
文章は「乗法の使われる場面は」から始まり，正比例型，複比例型，倍拡大型の3つを挙げています．式も例示されていて，順に「2m/分×3分＝7m*2」「2g×3m＝6gm」「2m×3＝6m」です．p.72には以下のとおり，それぞれの図式が載っています．

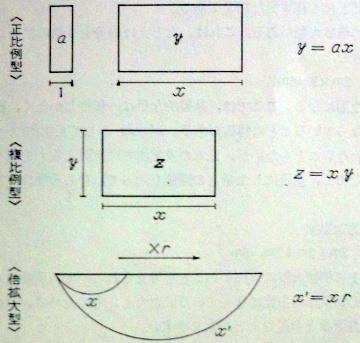
倍拡大型や，累加*3について，森は批判的です．囲みの記事は「図式的に書けば（図省略）とでもなろうが，乗法というのは本質的に二次元的性格を持っているので，イメージとして倍拡大型に固執していては苦しい。(M)」で終えています．
発言をざっと見直すと，「構造」という言葉を使っているのは，2人のうち森のほうだけです．上の引用には「正比例の構造」がありました．もう一つ，取り上げておきます．

森　掛け算というのは、本来的にはその構造自身の中に積集合の構造が入っているわけですよね。だから交換可能なわけです。しかし、だいたい数学でも交換法則にこだわるのは掛け算でしょう。2×5と書くか5×2と書くかという問題は、ある程度習慣に規制されるんですが……。

対話としては，この「習慣」を受けて竹内が英語のツー・タイムス・ファイブとファイブ・タイムス・ツー，そして森は左側通行と右側通行に言及しています．

2. 2010年以降―渡会

この文献では「乗法的構造」という言葉が定義され，使用されていました(p.150)．

※2: 乗法的構造とは、解決に乗法・除法が関わる問題場面全体の集合であり、単比例の構造とは、正比例の関係にある2つの測度空間で構成される構造である。

元にしているのは，Vergnaud (1988)のほうです．ふむ，multiplicative structuresを乗法的構造と訳したのか，「的」が特徴的だなと思い，CiNiiでこの著者によるものを探していくと，この内容が詳細化され，査読付きの論文になっていました．

それで本文を見ていくと，そこでは(p.5)

概念野理論において，乗除法は「解決に乗法・除法が関わる問題場面全体の集合」(Vergnaud, 1983, 1988)と定義される乗法構造において説明される．

と，「乗法構造」になっていました．論文化とともに「的」が抜け落ちたのでしょうか．
内容に関して軽く言うと，かける数が小数になるかけ算，わる数が小数になるわり算（のうち包含除）について，今のカリキュラムでは問題があるのではないですか，と主張しています．かけ算に対する解決案は，「比例関係」の充実です．「比例」そのものは6年で学習しますので，それを陽にしないという意味で，「比例関係」としているのでしょう*4．
森による囲み記事と，比較できるほうがいいですね…渡会(2010)では，「正比例の関係」の図を，次のように示しています(p.146)．


本日は，2013年はトランプ配り，1988年はアレイの続きにあたります．乗法構造も関係してきます．
次は，乗法構造に関してこれまで見てきた文献を整理し，遠山啓の著作と結びつけて，検討を図ることにします．

（最終更新：2013-10-12 晩）

*1:この次のトピックは「◎なぜ複比例はむずかしいか」です．p.77では「一説によると，プロダクトの概念とマルティプルの概念はちがうんだという」と森が発言しています．このころから，当ブログで2年ほど前に問題意識を持った「倍の乗法」と「積の乗法」があったのを，知ることができたのが，この本を得た一番大きな成果です．

*2:原文ママ

*3:式の例は「2m＋2m＋2m＝6m」(p.71)です．これの延長上に倍拡大型の乗法があると述べたのち，欠点として，0の処理や，操作と量との混乱を挙げています．

*4:1年の，繰り上がりのあるたし算で，さくらんぼ計算がうまくいく（他の方法と同じ答えになる）のは，加法の結合法則のおかげですが，1年生の子どもたちが加法の結合法則を学習するわけではないのです．