わさっきhb

大学（教育研究）とか ，親馬鹿とか，和歌山とか，とか，とか．

「倍」と「積」から学んだこと

5×3

目次

  1. 前回から，どんな変化がありましたか?
  2. 「倍」と「積」とは何ですか? 辞書の意味と違うのですか?
  3. どうして，「倍」と「積」を区別するのですか?
  4. 《倍の乗法》と《倍指向》，《積の乗法》と《積指向》は別物ですか?
  5. 《…指向》と《…の乗法》は，鶏と卵の関係でしょうか?
  6. 《倍指向》と《積指向》の具体例は，ありますか?
  7. 《倍指向》と《積指向》は，あなたの思いつきでは?
  8. 《倍指向》と《積指向》が同等であるとは，どういうことですか?
  9. トランプ配りが《積指向》という点について，詳しく説明できますか?
  10. 《倍指向》と《積指向》には，起源，または数学的な裏付けがあるのでしょうか?
  11. 結局，《倍指向》のほうが《積指向》に優るのでしょうか?
  12. 長方形の面積で，横×縦にバツをつける先生がいることについて，どう思いますか?
  13. 順列の式では，「幾つ分×1つ分の大きさ」になるのでは?
  14. 「1あたり量×いくつ分」ではいけないの?
  15. 日本の算数教育は「1あたり量×いくつ分」になっているのでは?
  16. 宮下氏の主張に賛成ということですか?
  17. 金田氏の論文は信頼できない
  18. 量の交換法則を認めないのは変だ
  19. 内包量は加法性を持たないってのは変ですよね?
  20. 外国で，かけ算の順序が反対だとバツにする事例はありましたか?
  21. 英語の本や有料のPDFファイル，入手困難な紀要や書籍を出典にするのはずるい
  22. 「100ワット×2時間」と「2ワット×100時間」は区別しなくていいの?
  23. 「式の意味」と「乗法の意味」は違うのですか?
  24. 「かけ算の順序」が「マイナスイオン」だなんて，何を馬鹿なことを言っているのですか!
  25. トランプ配りでかけ算を理解している子どもがいたとき，その考えを認めますか? それとも，かけ算の順序を矯正しますか?
  26. 小学校のかけ算の教育を理解するために必要なことは何ですか?
  27. これで，文献調査・Q&Aづくりは終わりですか?

1. 前回から，どんな変化がありましたか?

その後「×」から学んだことをリリースしてから，やはり，ずいぶんと変化がありました．英語文献を通じて，世界レベルでのかけ算指導の一端を学ぶことができました．被乗数と乗数を区別することの意義を確認するとともに，乗法（かけ算）が適用され，式で表される対象が，「被乗数と乗数を区別する」ものと「被乗数と乗数を区別しない」ものに分けられることを知りました．
当雑記においては，出題例のエントリに対して20ほどのはてブをいただきました（批判的なものが多く見られましたが）．着想を得て，いくつか新たなプログラムを作ったのも，いい経験でした．
関連：その後「×」から学んだこと・毒編，3分で「かけ算の順序」，プラス5分で「乗法の意味理解」，論文から学ぶ乗法理解，日本の「かけ算」，世界へ・世界と，出題例から学ぶ，乗法の意味理解，聞いた見た書いた，九九文章題ジェネレータ“99qg”をリリース，KWIC表示のbookmarklet，「順序」探し，「5個の4つ分」をRubyで

2. 「倍」と「積」とは何ですか? 辞書の意味と違うのですか?

「倍」は，「倍概念」などと書くときの「倍」と同じで，goo辞書のこちらの倍の1の意味に書かれている「同じ数量を重ねること」に該当します．ただし，学年が上がるにつれ，乗数すなわち倍率にあたる数は，整数に限らない（正の整数をもとに，より大きな範囲の数の集合に拡張される）ものとします．こちらの倍の意味ではありません．
「積」は，goo辞書の積の3の意味，すなわち「二つ以上の数や式を掛け合わせて得られる数や式」と同じと言っていいでしょう．ただし，積（かけ算）によって得られた値というよりは，「×」を含む式に焦点を当てます．
例えば「3×5＝15」という式において，積は，「15」ではなく「3×5」を指すわけです．この考え方は，「一つの数をほかの数の積としてみる」（《算数解説》p.81）に合致します．

3. どうして，「倍」と「積」を区別するのですか?

かけ算の指導に関する国内外の文献を読んでいたときに，その区別がなされているものを目にしたからです．
場面の例とその分類がもっとも充実しているのは，[Greer 1992]です．10月13日に，主要部分の訳出を試みました．
自分なりに調査・検討して至った成果は，次の通りです（《…》の定義については，あとの質問・回答をご覧ください）．

  • 《倍指向》と《積指向》の同等性を確認しました．これは，式として表わすのに関しては，「一方にできてもう一方ではできない」というものはないことを意味し，数学的・論理的には「どちらでもよい」ということになります．
  • 実際の指導においては「倍」が先にあることを，確認しました．日本の算数指導は《倍指向》ですし，海外においても《倍の乗法》が《積の乗法》よりも先に示されています．
  • 「さらが ５まい あります。１さらに りんごが ３こずつ のって います。りんごは ぜんぶで 何こ あるでしょう。」という問題に対して，「5こ（それぞれのさらに1こずつ），5こ，5こ」と乗せることで，「5×3＝15」も正解になると主張する，トランプ配りの考え方には，《倍指向》で立式の過程を説明していても，《積指向》が含まれていることを，見出しました．

4. 《倍の乗法》と《倍指向》，《積の乗法》と《積指向》は別物ですか?

それぞれペアになりますが，別物です．
定義を示します．

  • 《倍の乗法》：被乗数と乗数が区別され，「b×a」と書くと，「a×b」とは式の意味が異なるとされるかけ算のこと．
  • 《積の乗法》：被乗数と乗数の区別は本質的ではなく，「b×a」と書いても，「a×b」と同じ場面や対象を表していると解釈できるようなかけ算のこと．
  • 《倍指向》：《倍の乗法》に基づいて，乗法を意味づけるべきだという考え方．もしくは，かけ算で表すことのできるどんな場面や対象も，《倍の乗法》に帰着できるという考え方．
  • 《積指向》：《積の乗法》に基づいて，乗法を意味づけるべきだという考え方．もしくは，かけ算で表すことのできるどんな場面や対象も，《積の乗法》に帰着できるという考え方．

そのもとで，《倍の乗法》と《積の乗法》は，解く（かけ算の式で表わす）べき対象と記述される式に重点を置いています．一方，《倍指向》と《積指向》は，かけ算の式で表わす際の認知モデルと言えます．

5. 《…指向》と《…の乗法》は，鶏と卵の関係でしょうか?

いえ，先に目に見えるのは，《倍の乗法》と《積の乗法》であり，「サンドイッチ」や「トランプ配り」を含む様々な問題解決法を通じて，認知レベルに持って行くと，《倍指向》と《積指向》に至ります．

6. 《倍指向》と《積指向》の具体例は，ありますか?

《倍指向》には，累加と，比（または割合）の3用法が挙げられます．累加（「同数累加」とも言います）により，3×5＝3＋3＋3＋3＋3，5×3＝5＋5＋5と表されます（[中原2011] p.113）．3用法の中で第2用法はかけ算の形，例えばA＝B×pとして表されますが，baseになる数は×の左に，proportionになる数は右に書きます．《算数解説》では「3用法」という用語が陽に出現しないものの，pp.166-167に，乗法・除法の意味の拡張と結びつけて，3用法に対応する3つの式が挙げられています．
《積指向》としては，離散的にはデカルト積（直積），連続的には面積を利用するものが挙げられます．なお，数学教育協議会が推進する「面積図」（「かけわり図」とも）は，見る限り被乗数と乗数の区別をつけた図式であり，《倍指向》に分類するほうがよさそうです．
「3に5をかける」は《倍指向》，「3と5をかける」は《積指向》です．

7. 《倍指向》と《積指向》は，あなたの思いつきでは?

名称は独自につけました．《倍指向》と《積指向》は対外的（具体的には，数学教育の専門からの議論）には必要ないかもしれません．
《倍の乗法》と《積の乗法》の存在（「乗法の意味」の中でこの2つに分けられること）に気づいたのは，[岸本2000]の「倍(multiple)に関する小数の乗法を考察の対象とし，積(product)に関する小数の乗法は取り上げない」であり，その分類について，妥当性を得るに至ったのは，[Greer 1992]です．

8. 《倍指向》と《積指向》が同等であるとは，どういうことですか?

次の2つを示しました．

  1. 《積の乗法》の各場面について，《倍の乗法》に帰着することができる．
  2. 《倍の乗法》の各場面について，《積の乗法》に帰着することができる．

《積の乗法》から《倍の乗法》へは，次のようにします．

  • アレイ図*1におけるドットの計数については，「一つ分の大きさ」と「幾つ分」を見つけるよう，囲い込みをします．その囲い込み方に応じて，《倍の乗法》で式が定まります．
  • 長方形の面積について，縦横の長さが整数のときは，単位正方形の個数を数えます．整数でない場合は，例えば，単位正方形を縦方向にのみ伸縮させ，ついで横方向にのみ伸縮させれば，それぞれの図形および面積を得ることができます．
  • デカルト積（または直積）に基づく場面では，その対象に応じて，「一つ分の大きさ」と「幾つ分」を見つけることにより，式*2を得ます．
  • 電力量など，物理量の乗法については，単位正方形と同様に，得られる量に関する単位量を定め，あとは元になる（2つの）量が，何倍になるかによって，式を得ます．

《倍の乗法》から《積の乗法》へは，次のようにします．

  • 整数の乗法は，アレイ図で表します．
  • 小数や分数を含む場合は，複比例の関係y＝k×a×b（yはaに比例する．yはbに比例する．aとbは独立である）で表します．なお，k＝1のときはy＝a×bです．

9. トランプ配りが《積指向》という点について，詳しく説明できますか?

はい．「さらが ５まい あります。１さらに りんごが ３こずつ のって います。りんごは ぜんぶで 何こ あるでしょう。」に対する，トランプ配りの手順は次のとおりです．

“皿に順にりんごを配るのをイメージすると”…分かりにくいですか．まずお皿を5枚，用意します（手で大きな丸を5つ描く）．次にですね，りんごを，まず1個ずつ，それぞれのお皿に乗せます（描いた「皿」それぞれの上に，小さな丸を描く）．2回目（同），3回目（同）と配っていけば．「さらが ５まい」で「１さらに りんごが ３こずつ」という状態になります．ちなみにこれは，皿にりんごを乗せていくと言うより，トランプで，カードを参加者に順に配っていくのを想像するのがいいでしょう．「トランプ配り」と呼ぶ人もいます．

2010年12月25日（余談で話す）

この操作により，「3が『一つ分の大きさ』で5が『幾つ分』」という出題意図とは別に，「5が『一つ分の大きさ』で3が『幾つ分』」にも解釈できる，という主張です．
その理路として，次の2つ（3つの図解）が考えられます．一つの考え方を図にすると，以下のようになり，左端のアレイ図が，出題の場面に対応します．

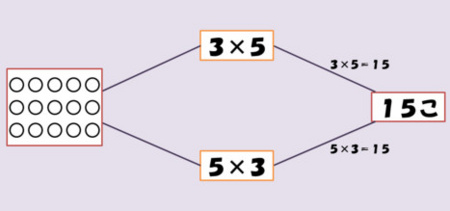
上の図を，「一つ分の大きさ」と「幾つ分」が明確になるよう変更すると，2種類の図になります．


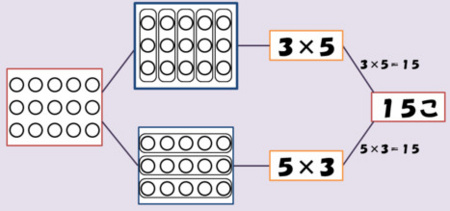
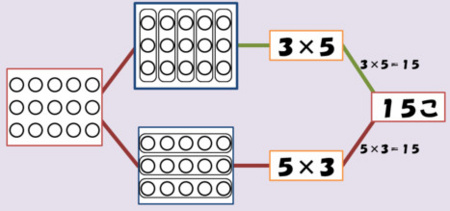
2つの図の違いは，出題の場面を，左端の（囲い込みのなされていない）アレイ図とするか，左から2列目の上のアレイ図とするかにあります．別の言い方をすると，左端のアレイ図が，場面をイメージするときの「起点」であるか「途中経過」であるかという違いです．
いずれも，「3が『一つ分の大きさ』で5が『幾つ分』」を意味するアレイ図と，「5が『一つ分の大きさ』で3が『幾つ分』」を意味するアレイ図を得ることができ，「3×5＝15　15こ」だけでなく「5×3＝15　15こ」も正解となる，というプロセスです．
[遠山1972]; [遠山1978] pp.114-116で，「6人のこどもに，1人4こずつみかんをあたえたい．みかんはいくつあればよいでしょうか」に「6×4＝24」をバツとする出題に対して，「教室の机は1列に6つずつ4列ならんでいます．机はみんなでいくつありますか」を例示しているのは，これらの図式によって説明ができます．

10. 《倍指向》と《積指向》には，起源，または数学的な裏付けがあるのでしょうか?

《倍指向》の具体例として挙げた「累加」は，ペアノの公理をもとに定義できます．正の整数a，bに対するa×bの定義は，以下によってなされます（[内海1980]; [新算研2011] p.121）．

(i) a×1=a
(ii) a×(b+1)=a×b+a
すなわち，aに1をかけるとはa自身のことであると定義し，a×2, a×3, ……は，2，3，…の定義と(ii)を用いて
a×2=a×(1+1)=a×1+a=a+a
a×3=a×(2+1)=a×2+a=(a+a)+a
……………
のように，順次同数累加として定義される．

量を対象とした場合，[高木2008] pp.213-246では，（一つの）量の空間をもとに，それに属する量どうしの比として実数を導いています．[Nagumo 1977]（その元となる論文は，日本語で1944年に書かれています）は，1つの量の集合Qに対して，QからQへの線形写像（自己同型写像）を定めると，その写像Φは倍率mと対応づけられることを示しています．
[田村1978]は，南雲の論文を継承しつつ，面積や速さといった，2つの量から得られる量についても検討しています．面積の単位は，縦と横の区別がないことが示唆される「f(L,L)」とし(p.51)，速さの単位のほうは，「f(T,L)すなわち‘時間Tに距離Lを動く速さ’を採用するのが便利である」(p.53)と，2者の区別があるような表記にしているのも，目を引きます．
《積指向》による，数学的な定義や数学教育の書籍は，目にしていません．ないわけではなく，もう少し具体的に書くと，《積指向》で乗法を導入して，成功しているという事例・書籍は，見かけません．その一方で，国内外の専門家が，次のように指摘しています．

累加の考えをさけようというのは，算数の指導についての基本的な立場の相異によることであって，乗法という問題だけで考察することは適切とはいえない．(略)しかし，乗法と加法の特別な場合を簡潔に表すという立場から意味づけることは，とくに，低学年の場合には，教育的にも意味のあることであり，さきのラパッポルト氏の反論にもある．
わが国でもこの立場をとっているが，アメリカの新しい計画による教科書でも，この立場をとっているものが多い．これには，ラパッポルト氏の指摘にもあるように，整数の段階では，集合の直積に近い意味づけをしても，累加の考えに帰著してほぼ処理できることや，直積の考えのままでは，実際に乗法を適用するに当たって，困難をともなうことなどの理由があげられよう．
（[中島1968b] p.76)

The Cartesian product is so nice that it has very often been used (in France anyway) to introduce multiplication in the second and third grades of elementary school. But many children fail to understand multiplication when it is introduced this way. The arithmetical structure of the Cartesian product, as a product of measures, is indeed very difficult and cannot really be mastered until it is analyzed as a double proportion. Simple proportions should come first.
（[Vergnaud 1983] p.135）

This class of situations corresponds to the formal definition of m × n in terms of the number of distinct ordered pairs that can be formed when the first member of each pair belongs to a set with m elements and the second to a set with n elements. This sophisticated way of defining multiplication of integers was formalized relatively recently in historical terms.
（[Greer 1992] p.277）

中国の教科書で被乗数と乗数の区別を廃止したという例がありますが，[国教研2009] p.181には以下のように書かれており，簡単ではないことがうかがえます．

乗法の学習は第2学年上半期に九九に伴って始まる。1つ前の教育課程から， 「一部分の学習者が被乗数と乗数の区別に難儀を感じる」，「中学校に入ったら被乗数も乗数も因数として扱う」などの理由で，被乗数と乗数の区別をなくし，最初から因数として扱うこととした(略)。これについて現場の授業等を観察したことがある。この処理は数計算の場合大きな差支えがないかもしれないが，量の扱いではやはり不具合があって，教師たちの丁寧な対応によって乗り越えているところである。

11. 結局，《倍指向》のほうが《積指向》に優るのでしょうか?

数多くの文献・事例を踏まえると，乗法の導入においては，

  • 《倍指向》がわかりやすい（立式も計算もしやすい）
  • 《積指向》で立式し，計算する必要性が見当たらない

と言えます．
一つ，理由を挙げてみるなら，《積指向》では「a×b」と「b×a」の2種類の式が，問題に対する正解の式になり得ます．そしてその中のどちらを選んで（または両方を）書けばよいのか，教える側・学ぶ側（学級内の先生・生徒に限定されません）の間で取り決めておかなければなりません．
ちなみに，《倍指向》は，式を一つにするために採用された，ということではありません．「何に何をかけて，何を求めるか」を明確にするためです．これには「演算決定」という用語が密接に関係します．乗法はどうあるべきかの議論は，乗法だけで語ってはいけないのです．

12. 長方形の面積で，横×縦にバツをつける先生がいることについて，どう思いますか?

小学校において，長方形の面積を導く*3のは，「《倍指向》で《積の乗法》」の典型例です．個人的には，「教え方次第」でありますし，「さらが ５まい あります。１さらに りんごが ３こずつ のって います。りんごは ぜんぶで 何こ あるでしょう。」は「《倍指向》で《倍の乗法》」の典型なので，同類にすべきではないと思っています．
さて質問ですが，「縦×横」のみを正解とし「横×縦」は間違いとするという事例を，主にWeb上の掲示板やブログのコメントで見かけますが，教科書・問題集・学習指導案・学力テストで文書化されたものに関して，見たことはありません．書店で目にしたいくつかの本では，両方を認めています．
ということで，横×縦にバツをつけることを不満に思うのなら，第三者検証が可能な事例を整理していただくことを期待します．
それと，《倍指向》であっても，（囲い込みのない）アレイ図におけるドットの総数をかけ算の式にするという出題では，「a×b」と「b×a」の2種類の式が正解となります．現在出ている多くの問題集にも見られ，そこでは，式をかける欄を2つ設けたり，解説に「（囲い込み方は）他にもあります」と記したりするなど，配慮がなされています．

13. 順列の式では，「幾つ分×1つ分の大きさ」になるのでは?

順列はデカルト積と最も関連が高く，《積の乗法》の典型例ですので，被乗数と乗数の実質的な区別はないと言っていいでしょう．[市川2011]では，順列や組み合わせが，《算数解説》で新たに加わった事項であると指摘した上で，具体的な出題に対して「計算による出し方は，軽く触れる程度にします」(p.104)，「ここでも計算は，深入りする必要はありません」(p.108)としています．
あえて，小学校の中で，順列の式を公式として導くのなら，「1つ分の大きさ×幾つ分」を用いることになると思います．その上で，「練り上げ」として，n個の異なった要素の中からm個の相異なる要素を選び出した順列が何通りあるか（n，mは文字ではなく具体的な整数）を，かけ算の式で表わすとき，因数を(n-m+1)から昇順で並べるのと，nから降順で並べるのとを，比較することがあってもいいと思います．

14. 「1あたり量×いくつ分」ではいけないの?

数学教育協議会で提唱されている，乗法の意味づけは，「1あたり量×いくつ分」（乗数は「いくら分」と書かれることもあります）または「内包量×外延量」です．
これには少なくとも3つの課題が指摘できます．

  • 「1あたり量」の児童への理解が大きな課題となります．そのことは，[手島1978]; [新算研2011] p.114や[日数教2011] p.75で指摘されています．また，「1あたり量×いくつ分」に基づき指導している先生の中でも，パー書きは使用しないという方針にした意図・事情が，[高村1997] pp.93-95，[銀林2011] p.145で見られます．
  • 上と関連しますが，パー書きの量とパーなしの量の相互変換が必要な場合があります．[関沢1993] p.81では「おり紙で，つるをおりました．私の班は，3人で183個のつるをおりました．これを同じ数ずつ分けたので，私の分は　183個÷3＝61個　になりました．」とし，「183個÷3人＝61個/人」を避けています．
  • 乗法の結合法則を学習する際，1あたり量どうしの積が出現します．次元解析などを知っている大人には造作のないことですが，3年生の児童に，パー書きの単位の一部が消えて新しいパー書きの単位が作られることの意義を知らせ，習熟させる必要があるかどうかというと，疑問に思います．

15. 日本の算数教育は「1あたり量×いくつ分」になっているのでは?

これまでの学習指導要領，そして日本数学教育学会（日本数学教育会）の出版物を目にする限り，文科省（文部省）による学習指導要領の作成・改訂，および教科書作成においては，「一つ分の大きさ×幾つ分」を基本としており，「1あたり量」の採用は見られません．言い換えると，「1あたり量」の指導は，現場教育で（教師らのノウハウの継承として）なされているものです．
「さらが ５まい あります。１さらに りんごが ３こずつ のって います。りんごは ぜんぶで 何こ あるでしょう。」に対して「3×5＝15」を得る際，1あたり量は「3こ/さら」，一つ分の大きさは「3こ」（そして式で表わす際には「3」）と表記されます．1あたり量の課題は，一つ前の回答をご覧ください．

16. 宮下氏の主張に賛成ということですか?

北海道教育大学教授の宮下英明氏のWebサイト([http://www.m-ac.jp/me/index_j.phtml])と，[http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20101123Kakezan.html]にある黒木玄氏の記述を読み比べれば，宮下氏の主張に賛成です．数学および数学教育学の土台のところが全然違います．

ただし，宮下氏の主張に全面的に同意かというと，そういうわけでもありません．まず「かけ算の順序」という言葉について，私は数学教育の学問で議論される対象となっていないと判断していますが，氏は私よりももっと時間をかけて研究され，何冊もオンラインブックを出されているにもかかわらず，この言葉の出自や学問的な妥当性について点検されたという形跡が見られません．
もう一つは，

に代表される，氏のかけ算の意味づけは，[田村1978]を読んで照合することで納得がいったのですが，オンラインブックを読む限りでこれらを典拠としていません．立脚点がないというのは，賛成を得られにくいようにも感じます．
私が書き連ねた中で，それまでの論者にない視点を見つけるとするならば，おそらく，工学のアプローチを採っていることだと思います．「a×bとb×aとでは答えは同じだけれど，式の意味が違う」という考え方もあれば，「たとえば犬の足を３×４の長方形型に並べて描いた模式図を思い浮かべて、長方形型にモノが並んでいる場合の全体の数をかけ算で計算できることを使えば、どちらがひとつあたりの数であるかを確定させることなく、正しい考え方で正しい答を出すことができます」という考え方もあるというときに，一方を正当なものとして他方に難癖をつけるのではなく，まずは対等に並べてみて得失を見ていき，どちらを採用すればいいかを判断する，ということです．《倍指向》と《積指向》が，形式上明らかに異なり対立するけれども，一方がもう一方に帰着できるという構図は，情報工学（情報科学）の学部・大学院での学習が基礎となっています．情報分野の例として，正規文法と有限オートマトンの等価性を挙げておきます．

17. 金田氏の論文は信頼できない

[金田2008]を信頼できないと判断している事例に，黒木玄氏によるhttp://www.twitlonger.com/show/bvsrd2があります．これは乗法の意味に関する異議であり，調査方法や結果の分析に対する問題点の指摘ではありません．なお，「大学生になってもかけ算を『被乗数×乗数』の順に書かなければいけないと考えるのは非常識だと思う」のところは，[中島1968b]（無料ではありませんが）を読むことで，数学と数学教育がどう関わるべきなのかを，もっと多くの人が考えてもいいのではないかと，思っています．
小学校の第2学年を対象とした，乗法の意味の量的な意識調査は，知る限り[金田2008]が唯一です．
乗法の意味に関する学習者の理解については，[Vergnaud 1983]にも事例が見られ，質的研究に位置づけられるものとして[高島2000]があります．乗数を整数から小数・分数へ拡張する際に，児童は適切に理解しているのかというのはわりと古くから見られる問題意識で，この点に関する，第5学年や教員志望の大学生を対象とした意識調査・理解度調査も，いくつか文献があります（[中島1968a] [今井1994] [岸本2000] [浅田2006] [小原2007] [齋藤2011]）．
といったところで，「かけ算ではかける順序はどちらでもいい」という主張に基づき，課題設定，国内外の関連研究，設問を含む実験方法，実験協力者（学校，教室）の選定，解答例の整理，統計処理，（結果を踏まえた）考察・展望に渡って，これらの実態調査に肩を並べるような研究成果を，誰がいつどのようにしてパブリッシュできるのか…静観したいと思います．
関連：←「かけ算の順序」←，Vergnaudと銀林氏の「かけ算の意味」，書くことは信じること - 5. あらためて，1968年の「被乗数×乗数」，「被乗数と乗数の区別」を調査 - 紀要，乗数効果，意識調査しないの？

18. 量の交換法則を認めないのは変だ

認めるには，少なくとも，次の2つのステップが必要です．

  • 「量に関する，乗法の交換法則」を数学的に証明する．
  • 「量に関する，乗法の交換法則」を小学校の教育で取り入れることの有用性を示す．

変だとおっしゃる方の手で，頑張ってください．
なお，交換法則の位置づけについては，[日数教2011]（第3章 教材論 §2 演算の意味・手続き）も参考になります．そこではまず，「小学校算数科における演算の意味と計算手続きに関する」(p.73)として，演算の意味すなわち立式と，計算手続きすなわち計算に分け，乗法の交換法則は計算手続きの中で言及しています(p.79)．

19. 内包量は加法性を持たないってのは変ですよね?

wikipedia:量の中の「外延量と内包量」「示量変数と示強変数」を読むことをおすすめします．
"intensive quantity"，"extensive quantity"を含む海外文献として，[Kaput 1985]があります．

20. 外国で，かけ算の順序が反対だとバツにする事例はありましたか?

見ていません．
近いところを挙げてみると，まず，坪田耕三氏がブラジルの子どもたちに6の目のサイコロを見せて目の数を式にしてもらったところ，ある児童が「3個ずつのかたまりを作ってそれが2つ分」を認識した上で，3×2と書き，他の仲間みんなが違う違うと言う，というエピソードがあります（[坪田2010] p.138）．
被乗数と乗数に当たる数が入れ替わると，難易度が変わることについては，"A rocket travels at a speed of 16 miles per second. How far does it travel in 0.85 seconds?"がその中の「16」「0.85」を交換したものよりも困難であるとして（また「乗数効果」の一例として），[Greer 1992] p.286に示されています．
全米学力調査(NAEP)を見たところ，Grade 4向け出題例のうちQuestion 7の解説の中で「316 x 4 = 1,264」という式が見られます．
それはそれとして…海外でその種の出題がないからといって日本で行うべきではないというのは，教育・文化の国家間の違いの理解に目を背けるものであり，国際的な視点に欠けているように思います．
「さらが ５まい あります。１さらに りんごが ３こずつ のって います。りんごは ぜんぶで 何こ あるでしょう。」と同種の問題によって，「1つ分の大きさ」と「幾つ分」を認識することの教育的な意義は，国内外の文献から確認できます．

21. 英語の本や有料のPDFファイル，入手困難な紀要や書籍を出典にするのはずるい

参考文献や立脚点を明示せずに書くほうが，何を考えているのか分からず，理解に苦しみます．

遠山啓や銀林浩氏の著書を重視する人の中で，「過去・現在の算数教育の実情」を把握できている人を見かけません．例えば，あとがき(p.118)で「かけ算の順序について，遠山啓さんや銀林浩さんの主張に疑問と批判を呈しましたが，数学教育協議会の量の考え方に学恩と敬愛を感じていることは変わりません」としている[高橋2011]を見てみると，二十といった数の表記の検討(p.19)に際して，十進位取り記数法がまったく出てきていませんし，「密度×体積＝重さ」と書くが「体積×密度＝重さ」と書かない(p.39)理由に関して，遠山は第2用法を挙げていることを無視しています．

22. 「100ワット×2時間」と「2ワット×100時間」は区別しなくていいの?

それぞれ，名数を含んだ式で書けば，明確に区別されています．
式の書き方として，100ワットの電力を2時間消費したときの電力量を「100×2」とすべきか「2×100」とすべきかというのであれば，「1ワット時」をどのように定義するかによります．
会計などに関して，「個数×単価」で書くよう指示があれば，そのルールに従うだけです．かけ算によって合計金額が得られるのは別の話です．

23. 「式の意味」と「乗法の意味」は違うのですか?

かけ算（乗法）で表わせるという限定があるとして，「式の意味」と「乗法の意味」には共通部分はあるが，同意語ではないと思っています．
「式の意味」とは「書かれた式*4が何を表すか」であり，基本的にはwhatの概念です．
一方，「乗法の意味」と書くと，「なぜその場面で，かけ算を使用して式を書けるのか」，すなわちwhyの概念を含みます．
小学校学習指導要領 算数の第2学年の中に，「乗法の意味について理解し，それを用いることができるようにする」の子要素として「乗法が用いられる場合について知ること」が記載されています．

24. 「かけ算の順序」が「マイナスイオン」だなんて，何を馬鹿なことを言っているのですか!

  • 「かけ算の順序」に疑問を持ち，インターネットで読める形にしたのは誰か
  • その人は，算数教育に関する実績・論文があるのか
  • 「かけ算の順序」をキーワードとする学術文献はあるのか

に注目すると，「かけ算ではかける順序はどちらでもいい」と「マイナスイオンは健康にいい」の同質性は，揺るがないと思っています．

25. トランプ配りでかけ算を理解している子どもがいたとき，その考えを認めますか? それとも，かけ算の順序を矯正しますか?

矢野健太郎が，遠山啓との関わりで書いた，以下の件ですね（[矢野1984] p.124)．

「矢野くんはやっぱり算数は素人だね．実際，矢野君の言うように考える子がときどきあるんだよ．われわれはこのような配り方を，カード式配り方と呼んでいるがね」

かけ算の式で表せるさまざまな場面において，「一つ分の大きさ」と「幾つ分」に相当する数がそれぞれ何になるかを見つけられるようにすることは，その後の学習においても，また日常生活においても有用であり，学習指導要領とその解説，また様々な文献・問題集など（2年生向けに限らず）を読んできた限り，1〜2年で学習することがもっとも有益と思われます．
その学習や理解を促す書籍が，去年と今年，1冊ずつ出ています．一つは[田中2010]です．順に解いていくことで，「文」「絵・図」「式」が結びつけられるようになるという問題集です．幾つ分の大きさが先に提示される，かけ算の問題も，入っています．
もう一つは[前川2011]で，問題集というよりは学習指導案の事例集となっています．p.66では，「具体物をまとめて数える」という授業例の中で，「子どもが3人います。みかんを1人に2こずつあげます。みんなでなんこいりますか」を出題しています．そこに書かれている，興味深い注意事項として，「1個ずつ置くか，2個ずつ置くかという置き方ではなく，置いた結果に着目させる」があります．児童がこれを理解できれば，問題文から「一つ分の大きさ」を発見しやすくなるように感じます．

26. 小学校のかけ算の教育を理解するために必要なことは何ですか?

真っ先に認識すべきことは，乗法は，小学校の算数の重要な位置を占めていますが，それが全てでも，端緒でもないということです．
「端緒でもない」について，もう少し書きます．乗法を累加とするか，加算とは別の演算として位置づけるかについては，数学教育協議会が問題提起をし，それと別に海外でも1960年台に議論がなされました．ですが現在の日本の算数においては，「累加の簡潔な表現」が《算数解説》p.87に明記されているほか，「まとめて数える活動」*5が同文書p.65およびp.80に見られ，乗法の素地として（当然ながら乗法よりも前に）学習している点を，無視するわけにはいかないと考えています．
小学校の算数教育全体で，どのような課題があり，またどのような提案や事例報告があるのかを知るには，今年出た[日数教2011]がおすすめです．乗法の意味に集中したければ，[新算研2011]です．

27. これで，文献調査・Q&Aづくりは終わりですか?

いえいえ．やっと，「これまでの状況」が見え始めたところです．
今後は，誤記などを修正していくとともに，各回答に関連する当雑記のこれまでのエントリをリンクする予定です．

参考文献

*1:もしこの言葉を初めて知ったという方は，《算数解説》をダウンロードして，p.81の「●」の配置をご確認ください．これがアレイ図の例です．この図式には，「アレー図」「ドット図」といった別称もあります．当雑記では「長方形的配列」と書くこともありました．

*2:「場合の数の積の法則」となります．なお，この法則（公式）は，小学校の範囲で扱われず，代わりに「指導に当たっては，結果として何通りの場合があるかを明らかにすることよりも，整理して考える過程に重点をおき，具体的な事実に即して，図，表などを用いて表すなどの工夫をしながら，落ちや重なりがないように，順序よく調べていこうとする態度を育てるよう配慮する必要がある。」（《算数解説》p.211）と記されています．

*3:長方形の面積を得たら，何指向だとか何の乗法だとかは意識せず，その公式で面積を求められます．そして平行四辺形や三角形などの面積に応用されます．

*4:センテンス型ではなくフレーズ型の式を指します．「3×5＝15」ではなく「3×5」です．

*5:2とび，5とび，10とびから始まって，任意の数を「一つ分の大きさ」として数えることです．英語ではskip counting（[Yoshida 2009]）と表現するようです．