配る

1. かけ算の順序に気をつけましょう

「かけ算の順序」は，それを批判する人々の中で発生・展開してきた言葉です．「掛け算」「順番」などのバリエーションも見られますが，『かけ算には順序があるのか』の本，そしてwikipedia:かけ算の順序問題から，Web上では「かけ算の順序」の言葉が，どんな問題なのかを知る糸口となっています．
その一方，数学教育の研究や学校現場の実践の中で，「かけ算の順序」の使用は，批判する人々ほど多くありません．その話を含む用語は「乗法の意味」や「被乗数と乗数の区別（かけられる数とかける数の意味・ちがい）」になります．かけ算の「順序」については，別の使われ方があることを，こちらで整理しています．
しかし，「使用しない」とも言えません．いくつか出現例がありまして，もっとも明確なのは文献：馬場2002でしょう．
そんな中，手にした問題集には，解答・解説のところで「★かけ算の　じゅんじょに　気を　つけましょう。」という注意書きが何回か，書かれていました．

ハイレベ100小学2年算数

さっそくですが該当箇所です(p.126)．

「りんごを　1人に　3こずつ　7人の　子どもに　くばります。ぜんぶで　何こ　いりますか。」に対する式は「3×7＝21」です．3と7と取り出して，かけ算の式にしたら出来上がりです．
「子どもが　8人　います。1人に　4本ずつ　えんぴつを　くばります。えんぴつは，ぜんぶで　何本　いりますか。」だと「4×8＝32」です．こちらでは，4を先（かけられる数），8を後（かける数）として書くことが，求められています．
この本で「★かけ算の　じゅんじょに　気を　つけましょう。」と書かれているのは，上のを含め5箇所あり，そのうちの3つが，「配る」場面での問題です．
これはやはり，配ることが子どもたちにとって---教室でも家庭でも---容易に行えるからなのでしょうね．

2. Allocation

「配ること」には，累加やグルーピングとは別の，かけ算の構造があると，Anghileri 1988に書かれています．取り出して私訳を加えました．

Allocation/Rate---Multiplication

This arises when there is a many-to-one matching in which equal sets (portions) are matched using a tally of objects (owners). The example in Fig. 6-12 shows three cats each with two fish.
At first, this may appear to be identical with the previous equal groupings. Note however the presence of a tally set, the cats, which in fact makes it easier. Young children find it easier to "give two candies to each doll" (three dolls) than to "make three equal portions of two candies". The language of matching is more familiar to them, and the presence of a tally set means that only one of the two numbers involved needs to be internalized and acted on.
（配分・割合のかけ算
これは，同じ数のひとまとまりが，対象物の割り当てによって対応づけられる，多対一のマッチングがあるときに生じる．図6-12の例では，3匹の猫が2匹ずつ魚を持っている．
これは直前の，同等のグルーピングと同じものであるように見えるかもしれない．しかしながら，猫という，配られる対象の存在が，場面の理解を容易にしていることに注意したい．幼い子どもたちには，「2個ずつのキャンディが3つある」よりも「3匹の猫の人形に2個ずつのキャンディをあげる」ほうが，分かりやすい．マッチングの言葉は親しまれており，そして配られる対象の存在が，出現する2つの数のうち一方だけを内面化し影響を与えるものとなっている．）
(pp.159-160)

（メモ; matching: allocationの言い換え; many-to-one matching: それぞれに同数のものが配られている状態＝1匹の猫に2個のキャンディが配分されている状態; presence: 実際の操作（配ること）をしたり，総数を求めたりするより前に，明示されていること; a tally set: 3匹の猫＝配られる対象; the language of matching: マッチング（対応づけ，配分）の概念（子どもたちは必ずしもきちんと言語化できないが，操作ができ，イメージを持っている））
要所となるのは，強調した「the presence of a tally set, the cats, which in fact makes it easier」「猫という，配られる対象の存在が，場面の理解を容易にしている」のところです．そして，「three equal portions」が抽象的で分かりにくいもの，とつながっていきます．
言葉で表したときの「数の出現」を見ておきますと，「"give two candies to each doll" (three dolls)」では，2（かけられる数）が先，3（かける数）が後*1なのに対し，「"make three equal portions of two candies"」では，3（かける数）が先，2（かけられる数）が後となっています．
その一方で，上のallocationの説明には，その状況を式で表すとどうなるかが，書かれていません．「make three equal portions of two candies」については，2＋2＋2あるいは3(2)と書くことが，前ページの内容から期待されます．At firstから始まる文を見ると，著者あるいは算数指導をする際には，数量の関係は同型なので，やはり想定されているのは同じ式なのでしょう．彼らのかけ算にすると3×2，日本式だと2×3です．加えて言うと，「猫」に親しみを持っても，求めたい総数はキャンディの数なので，かけ算として考え，式を立てて答えを出すプロセスのどこかで，「three cats」を「three equal portions」へと変換（ある種の抽象化を）する必要が出てきます．
そういったことが，「配る」場面や出題を出す，日本の事例にも関係してくるように，思えます．
ところで，「Allocation/Rate---Multiplication」は小見出しなのですが，Rateの話は英文に一切出てきていません．これは，「A variety of Contexts」(pp.158-163)のトピックの一つだからです．そこに現れる小見出しを，出現順に並べておきます．

• Equal Groupings---Multiplication
• Equal Groupings---Division
• Allocation/Rate---Multiplication
• Allocation/Sharing---Division
• Number Line---Multiplication
• Number Line---Division
• The Array
• Scale/Multiplying Factor
• Scale/Reduction Factor
• Cartesian Product

おそらくRateの語は重要ではなく，次の「Allocation/Sharing---Division」の「Sharing」と釣り合わせるために，入れたのかなと思っています．

3. 猫にキャンディ，3×2とできるか?

上述の猫にキャンディの場面で，日本式でも，3×2を正解とする根拠がいくつか知られています．

• トランプ配りとして知られる方法で，「3匹」を「3個」として，かけられる数を読み替える．
• Vergnaudの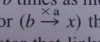の考え方を用いる．「×2」を，猫の数からキャンディの数へ変換する作用素とみなし，かけられる数（基準量）は3匹で変更しない．
• 複比例を用いる．

それぞれについて，学校で採用されていない理由も書くことができます．トランプ配りの乗法への適用は，遠山が示した後に算数教育において検討がなされておらず，国際的にも認知されていません．作用素（あるいは関数関係に基づく乗法）や複比例は，低学年の範囲を超えています．
（追記; 「交換法則を使用する」「アレイ図にする」も，あるのでした．それらを，演算決定や立式の根拠に採用しないのは，日本の算数での了解事項と言っていいでしょう．批判に対しては，それらを活用した指導法の提案---小学校で利用可能な形で---をお願いすることにします．検討に際しては，これまでの指導・学習をどのように置き換えるか，「小数×整数」「分数×整数」のタイプの場面でも適用できるか，の確認も期待したいところです．）
低学年の学習では，「被乗数と乗数を明確に区別して扱っている」「表現という側面からは被乗数と乗数の意味が特に重要」「立式ができているかで，数の読み取りができているかを判断できる（ように授業・テストをしている）」「まとめて数える」「2×3と3×2が異なる場面をつくる」により，2×3となることが共有化されています．
「配ること」に関して，

低学年の子どもは自分のイメージを上手に説明できるとは限らない。さらに教えている教師の側にはトランプ配りのようなイメージで被乗数と乗数の概念を理解する方向に進んでいる子どもは存在しないという強い思い込みがある可能性がある。このような場合には教師の「存在しない」という発言は必ずしも信用できない。家庭内でおやつをトランプのように配っていた家庭の子どもが実際にそのようなイメージで乗数と被乗数を理解している場合が存在することもわかっている。「発言小町：小学2年生、掛け算の文章題で悩んでいます。」におけるトピ主の発言を参照されたい。そこを読むだけで「どのような問題があるか」がかなりわかるので長々と抜粋しておこう。（たとえば相談したトピ主に回答者たちが単位サンドイッチ論法について教えてしまっていることがわかる。）赤字による強調は抜粋者による。

算数の教科書とその指導書の問題点

から始まる指摘も見られますが，読んでみると，「配り方」は分かるけれど，それをかけ算の式にする話とつながっていませんし，「配ること」をかけ算の構造として，お子さんが認識しているように見えません．そもそも親の質問の仕方にバイアスがかかっているため，この例によって，「配ること」がかけ算の素地（もしくは，お子さんの持つ，かけ算のイメージ）であると主張するには，無理があります．
そして，「娘は自信満々で、全問、数字を逆に書いていました」「完全に図式が逆に成り立っていたようです」から，状況は，「式の意味を間違えて覚えている」と考えられます．状況確認と対処法については，年末に整理しています．

4. アレイ

ここからアレイ(Array)に視点を移します．冒頭の本のp.139に，興味深い問題と解説があるのでした．

「よこ　1れつに　5人の　子どもが　ならび，その　後ろに　それぞれ　3人の　子どもが　たて　1れつに　ならんで　います。子どもは　みんなで　何人　いますか。」です．5と3をかけて「5×3＝15」としてはいけないんだよ，という意図が読み取れます．
正解としている式には，「3×5＝15　5＋15＝20」のほか，カッコ書きで「1＋3＝4　4×5＝20」とあります．いずれも，「×5」が入っており，ここから，問題文中の「5人」が，かける数になるのだなと理解できます．
アレイの話なのだから，「5×3＝15　5＋15＝20」*2としてもいいのでは…と当初，思ったのですが，かけ算については，「向山型算数」読み足しで見た，イスの問題と同型になっていることに気づきました．「たて　1れつ」がひとまとまりで，その数が，かけられる数となります．
網掛けになっているアレイもよく見ると，縦の列では●○がほぼくっついていて，列ごとには隙間があります．

5. かけ算の場面の，より細かい分類

Anghileriの解説では，pp.164-165に，乗除算をタイプ分けした表があります．表内の見出しのうち，

• Equal Grouping（同数のグループ，グルーピング）
• Allocation（配分）
• Array（アレイ）
• Cartesian product（デカルト積）

によって，整数を対象としたかけ算が使われる状況，あるいは乗法の構造（モデル，概念）が，より詳細化できるように，感じています．
ここで比較しておきたいのは，Greer 1992です．そこでは，〈乗数と被乗数が区別される文脈〉と〈乗数と被乗数を区別しない文脈〉とに大別しています．Arrayについては，他の文献紹介と図から，後者になることが読み取れます．Allocationについても言及は見当たりませんが，分類表の中でもっとも近いのは「Equal groups」であり，乗数と被乗数が区別されるほうです．
といったわけで，整数の乗法の分類としては，GreerよりもAnghileriのほうが，より詳細化されています．
もう一つ，重ね合わせたいのは，遠山の「6×4，4×6論争にひそむ意味」です．簡単にいうと，配分とアレイがともに，ある式だけでなく，そのかけられる数・かける数とを交換した式も，正解（その場面を表した式）であると主張しています．
そんなこんなで，分類表ができそうだと思い至りました．上記の4項目を行，「1つの式」と「2つの式」を列とし，各文献，日本の算数やその批判者を含めたそれぞれで，各場面がどれに対応するかを，該当するマスに乗せるのです．概略としては，左上から右下への緩やかな「賛同者」の流れができます．批判者はいずれにおいても，2つの式です．
試作した表は次のとおり．色は，そこに該当する，賛同者の割合でもいいですし，出題の割合*3とすることも可能です．濃くなれば「多い」「高い」です．表の構成や配色は，ぼくのかんがえた Multiplicative Structuresで作成したものを使っています．

配慮すべきことが2点，あります．デカルト積に関係する問題は，日本の算数では，整数を対象としたかけ算の中でほとんど見られず，学習するとしたら6年です．するとその段階では，全国学力テストの「乗数と被乗数を入れ替えた式なども許容する」を考慮しないといけません．

アレイも要注意で，向山型算数で確認したとおり，「1つの式」にも「2つの式」にもなり得ます．より正確には，どちらになるのかは出題に依存します．縦横の距離が均等な図をもとにすれば2つの式，「ずつ」を含む文章題であれば1つの式になります．米国のCommon Core State Standards for MathematicsのArrayの扱いも，同様になりそうです．

（最終更新：2013-01-16 朝）

*1:海外でも「かけられる数」と「かける数」の区別があるのか，という疑問に対しては，Greerが"3 children have 4 cookies each. How many cookies do they have altogether?"を挙げた直後に"Within this conceptualization, the two numbers play clearly different roles. The number of children is the multiplier that operates on the number of cookies, the multiplicand, to produce the answer."と述べていることから，「ある」が答えとなります．

*2:アレイで考えると被乗数と乗数は交換可能，合併の加法なので被加数と加数は交換可能，とすると合計4つの式が思い浮かびます．

*3:a×bのかけ算の式で求められる問題を国内外から集めてきて，自分がそれを8つのマスに振り分けたらどうなるか，を想定しています．