によると,学校図書の算数の教科書には,「ならび方が何通りあるかを,計算で求める」という,力だめし*1の出題があります.
「Aさん,Bさん,Cさん,Dさんの4人の子どもがいます。4人がならぶと何通りのならび方があるか考えましょう。」という問題です.かきかけの樹形図のほか,「□×□×□×□」という,穴埋めのかけ算の式があります.式として,期待されるのは,「4×3×2×1」です.というのも,この式の上には「□に数を入れて,あおいさんがどのように考えたのか書きましょう。」という指示が,そして下には次のようにセリフが,それぞれあるからです.
1番目は4人のうちの1人を決めるので,
4通りの決め方があるね。
2番目は,その1人に対して
3通りの決め方があるね。
ということは,2番目までは
4×3通り
あるんだね。
(転載元)
このような問題設定では,式に「1×2×3×4」と書くのは無理があります.あおいさんの「4×3通り」にも,図の1番目から4番目までの配置(関連:4+4+3+4=15と4+3+4+4=15)にも,合わないからです.
順列のかけ算については,当ブログで以前に検討をしています.書くことは信じることでは,「場合の数の積の法則」を暗に使用していることや,式に添えられる単位について指摘するとともに,1番目から4番目までの並べ方を樹形図ではなく表にしています.なぜ教材研究では,割合の第2用法を根拠として「4×3」になることを確認したほか,「4×3×2×1」と「1×2×3×4」との比較を試みています.
ところで,同型に見える2つの樹形図から,乗法構造の違いを知ることができます.
教科書ではなく別の本を使いましょう.『かけ算には順序があるのか (岩波科学ライブラリー)』p.18には,次のように2つの絵を横並びにしています.

図1は,学校図書の「4×3通り」と同じで,A,B,C,Dから2つを取り出して並べる場合の数です.図2は,6人に4個ずつミカンを配るという図です.
ここで図1の数量の関係は,次のような表であらわすことができます*2.

1番目だけの「4」通りと,2番目までの「12」通りが,同じ行に位置します.
それに対し,図2の関係は次のようになります.

人数の「6」人と,ミカンの数の「24」個は,列が同じであり,行は異なります.
この違いは,次の2つのSCHEMAに対応します(次のステップ).

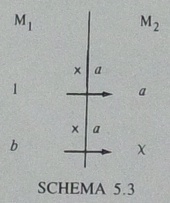
「同じ量空間での乗法関係」と「異なる量空間での乗法関係」という違いがあります.『算数・数学科重要用語300の基礎知識』p.187では,「スカラー関係に基づく乗法」と「関数関係に基づく乗法」と書かれています.なお,同書およびVergnaud (1983)をもとにすると,ミカンの数を表す式は6×4ではなく4×6になります.
乗法構造としての主要な違いは,ここまで書いたとおりですが,順列(図1)と配る話(図2)には,まだまだ違いがあります.順列については,「3番目まで」と一つ増やしたら,場合の数は「×2」となります.というのも,4人から2番目までが決まっている状態では,3番目は残り2つから選ぶことになるからです.しかしミカンのほうには,そのような制約はありません.どのミカンも同じ数の房があるとしても,それは配られる人数や,1人に何個ミカンを配るかには依存しないのです.人数・個数の変更に応じて,房の数が変わるようなミカン,見たことありますか?
語順あるいは思考の順番にも,注意をしておきたいところです.配る話では,「6人に4個ずつミカンを配る」とも「6個ずつ4人にミカンを配る」とも言うことができます(これが,おやつの じかんや8マス関係表の基礎となっています).それに対し,1番目・2番目の件で,「2番目は3通りの決め方があるね。1番目は4通りの決め方があるね。ということは,2番目までは3×4通りあるんだね。」と言うわけにはいきません.1番目として何を選ぶかを決めていない状態では,「2番目は3通り」と言えないからです.
(2021年1月追記)本記事の内容をもとに,サブブログ(かけ算の順序の昔話)にていくつか記事を公開しています.合わせてご覧ください.