いきなりですが問題です.
小学6年生59,000人が受けたという算数のテストに,以下の問題がありました.
次の問題を読んで、答えを求める式を分数を使って書きましょう。
- 1mの重さが4kgの鉄のぼうがあります。この鉄のぼう
mの重さはどれだけでしょう。
公表された解答には「
または ■■■■■」とありました.「■■■■■」は,何でしょうか.
さっそくですが解答です.[tex:4\times\frac34=3]です.
といったところで元ネタです.東京都算数教育研究会(都算研)が実施したテストです.テストは年度末,おそらく今年の2月か3月に実施されており,集計結果の公表は,今月18日の研究発表会のあとです.
上の鉄の棒の問題は,第6学年,大問2の(2)です.これまでよく,URLに「#page=ページ番号」をつけて直接ページに飛べる書き方をしてきましたが,今回はそうしていません.というのも,このPDF文書には,第1学年の出題にページの重複があり,差し替えられる可能性があるからです.
さて,が正解として認められるかというと,その調査では否定的です.実際,出題と同じページには,「評価基準及び割合(%)」として,解答類型*1が記載されており,
には「C1」という,不正解のラベリングがなされています.
これは,2年前の学力実態調査でも出題されています.
その結果を受けて昨年度,公開された文書があります.そこでもやはり,誤答の最初にが記載されています.
を正解にしようという理路も,思い浮かんでいますが,先月2013年はトランプ配り,1988年はアレイで取り上げたとおり,交換法則の適用は認められない*2ですし,関数的に考えたとしても,この問題を解く児童らはすでに比例を学習しており,問題文に当てはめると,比例定数は4のほうです.
平成24年度実施の学力実態調査,「かけ算の順序」で見るべきなのは,第2学年です.問題提示の仕方が少し変わりました.
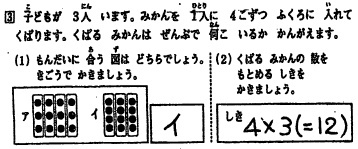
[3] 子どもが 3人 います。みかんを 1人に 4こずつ ふくろに 入れて くばります。くばる みかんは ぜんぶで 何こ いるか かんがえます。
(1) もんだいに 合う 図は どちらでしょう。きごうで かきましょう。
(2) くばる みかんの 数を もとめる しきを かきましょう。
前回(平成22年度実施)は,上でリンクした文書のほか,みかんの配り方で見てきたとおり,「くばる みかんの 数を もとめる しきを かきましょう。」と指示していて,文章題からただちに式を書かせています.今回はその間に,図を選ぶという小問が入っています.
変更した意図は,明記されていませんが,これは新しくなった教科書を踏まえてのものだというのが推測できます.学習指導要領の改訂は平成20年度,そして小学校算数の先行実施は平成21年度からでしたが,その学習指導要領に基づいた教科書が最初に出されたのが,平成23年度からなのでした.教科書を持っていなくても,そこでかけ算をどのように指導しようするのかは,東京書籍などで見ることもできます.
学習指導要領の改訂が2年の算数に影響したことと言えば,数量関係の領域が設定された点が挙げられます.文章,図,そして式を関連づけようという以下の記述は,以前の同解説には見られませんでした.
式に表す指導に際しては,「1袋に5個ずつ入ったみかんの4袋分」というような文章による表現,○やテープなどの図を用いた表現,具体物を用いた表現などと関連付けながら,式の意味の理解を深めるとともに,記号×を用いた式の簡潔さや明瞭さを味わうことができるようにする。
(小学校学習指導要領解説 算数編(平成20年6月,文部科学省)p.98)
学習指導要領や教科書とは別に,算数教育の実践の立場からも近年,その知見が文章化され,新たな出題や指導法が提案されています.かけ算の文章題のつまずきについては,昨年末に書いた文章の断片を挙げておきます.
このことは,[田中2009]と照合することでより明瞭となる.同書では,かけ算の式を間違える原因として,(1)文章を読んでイメージすることができていない,(2)式の意味を間違えて覚えている,の2種類を挙げ,「治療するところが変わりますよね」としている.この(1)は,かずや君の問題の「どうして,そのようなしきになったか,絵に書いて教えてください」,(2)は「こたえを出すためのしきを書いてください」に対応する.正答率の違いから,対策をすべきは(1)ではなく(2)のほうであることが理解できる.
「計算の意味の理解」の調査における一考察
「[田中2009]」とは,『田中博史の算数授業のつくり方 (プレミアム講座ライブ)』のことです.wikipedia:かけ算の順序問題でも,引用されています.また同氏の『筑波大学附属小学校田中先生の 算数 絵解き文章題 (有名小学校メソッド)』は,「文」「絵・図」「式」が結びつけられるようになるという方針で,図入りの問題が多数,収められています.
都算研の今回の出題変更は,そういったことを踏まえて,なされたものだと解釈することができます.
それで終わったら苦労はしませんで,このみかんの問題,「評価基準及び割合(%)」と解説の変更についても,見ておかないといけません.まず解答類型は,「A1:正答」「B1:(1)のみ」「B2:(2)のみ」「C3:左記以外の誤答・無答」と分けられています.平成24年度のところはいいとして,過去の平成22年度・平成20年度は,出題内容そして解答類型が変わったにもかかわわず,前回の集計結果から割合(%)が移動しただけのように見えます.
それから,平成24年度までの3回分の帯グラフを比較すると,C3が平成24年度に12%と,上がっていることも,不思議なところです.約6万人の12%ですから,7千人強が,(1)も(2)も正解できなかったことを意味しています(それまでは式だけ書かせる問題で,10%以下だったのに).もしかしたら,文章→図→式という出題の流れは,多くの解答者にとって経験がほとんどなく,そこで戸惑ったのでしょうか.
解説の文章に,「順」「順序」を含む,いわゆる「かけ算の順序」を匂わせる表現がなくなっているのも,気になります.具体的にはこうです.
乗数、被乗数の関係を考えて立式できるかをみる問題である。正答率は54%である。また、28%の児童は問題文に合った図を選ぶことができ、6%の児童は問題文から立式することができている。乗法の指導においては、問題場面を絵や図、半具体物に表す活動をとおして、「一つ分」に当たる数はどれかを視覚的に捉えたり、絵や図から「一つ分」を捉えたりすることが大切である。また、問題場面を絵や図に表す活動と絵や図を式に表す活動、式から問題場面を考える活動に取り組むことでかけ算の意味の理解を深めていきたい。
前回(平成22年度実施)はというと:
乗数、被乗数の関係を考えて立式できるかをみる問題である。正答率は54%である。36%の児童は問題文に出てきた順に立式したものである。乗法の指導においては、問題場面を絵や図に表すだけでなく、式を半具体物で表したり絵や図で表したりする活動や、身の回りの事象から乗法の式で表せるものを探す活動を通して、「1つ分×いくつ分」という関係が体験的にとらえられるようにしていきたい。また、問題文に出てきた順序と逆に立式する問題を取り入れ、「1つ分」に当たる数はどれかを考える態度を育てていきたい。
この違いですが,想像するに,「この問題,3×4ではダメなんだよ」という書き方を取り除いた,と読めば,まずはそれが,この調査結果を踏まえて教育改善にあたろうという先生方のためのアドバイスであり,あともう一つは,昨今の「かけ算の順序論争」への対応の仕方なのかもしれません.
他の学年で,かけ算に関して,インパクトのあるものは特にありませんでした.おはじきの総数を求める式を2種類書く問題は,第2学年大問4で,また逆思考*3にも注意してかけ算・わり算の式を選ぶ問題は,第3学年大問4および第4学年大問4で,それぞれ維持されていました.
今週,はてブのツイート連携で引用・リツイートをくださいました[twitter:@tsatie]さん,[twitter:@Higeow]さんの名前を挙げ,感謝するとともに,リプライをお送りします.http://twilog.org/Higeow/date-131025より,リツイート以降「posted at 07:17:51」から始まる一連のつぶやきについても,読ませていただきました.
感想にかえて,以前に書いた記事をいくつか並べることとします.