本文は内容的に古く,更新する予定はありません.かわりに以下の記事や文献が参考になれば幸いです.
- 積に基づく乗法の認識について
- 岸本忠之: 小数の乗法における学習状態の移行, 富山大学教育実践総合センター紀要, No.1, pp.1-8 (2000). http://doi.org/10.15099/00001082
- Greer, B.: Multiplication and Division as Models of Situations, Handbook of Research on Mathematics Teaching and Learning, National Council of Teachers of Mathematics, pp.276-295 (1992). https://books.google.co.jp/books?id=N_wnDwAAQBAJ&lpg=PR1&hl=ja&pg=PA276#v=onepage&q&f=false
1. はじめに
かけ算は,学校教育の縮図なのかもしれません.
誰もが小学校で,教育を受け,かけ算を学びます.大人になってからも,教育機関を通じて得た知識と,学校教育の外で身につけた技能を使いながら,毎日の生活を送り,成功や失敗の経験を,自らの知識・技能へとフィードバックしています.レシートに打たれた「@147×2点」から「147円の商品を2つ」と認識できるのは,学校内外の知識をうまく組み合わせているからです.
誰もが教育について議論できるように,かけ算についても,長年にわたって議論されています.ここ数年の,Web上の議論は,「かけ算の順序論争」です.
私は,その論争でよく巻き起こる展開に気を留め,またそのアウトプットを享受しつつも,関心は少し別のところに置いています.
新刊・復刊・古書による,20世紀に活躍した数学者らによる本や,算数・数学教育の実践家・研究者らによる論文・解説・授業案などを読んできました.
インプットだけでなく,アウトプットも,徐々に増やしていきました.新旧のアイデアや知見を組み合わせ,現状そして近い未来において,小学校で学ぶことが望まれているかけ算は何なのか,その輪郭を自分なりに描くことを,一つの目標として,ブログを中心にいろいろ書いていきました.
批判する多くの人々は,「かけ算には順序がない」という一枚岩に集結しているように,感じています.一方,これまでの先生方の著書を読んでいくと,どうやら小学校では,低学年では「累加」によって被乗数と乗数の役割,そしてそれぞれの違いを重視し,高学年になるにつれて「拡張」を行いながら,その区別を減らしていっているようです.複素数の範囲までで,乗法の交換法則が成立するという,数学的な要請も,もちろんあります.
2. 新たなサンドイッチモデルの提案
いくつかの本では,かけ算を「倍」と「積」の2つに大別できると説いています.「倍」のところをさらに分けるものもあります.
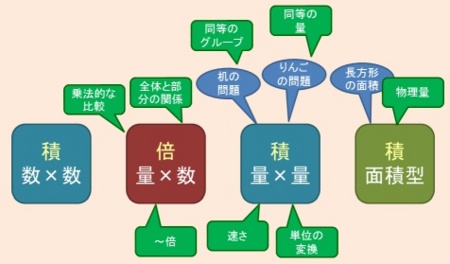
今回私は,「積」のほうを2つに分け,その間に「倍」を置くという,乗法の意味理解のための枠組みを提案することにしました.

このうち,従来から「積」として扱われてきたのは,「数×数」と「量×量」です.「数×数」には,純粋な数どうしのかけ算のほか,直積(デカルト積)に基づくかけ算が含まれます.
しかしながら「量×数」もまた,高木貞治の『新式算術講義』をはじめ,数学的に研究されてきました.日常においても,「20g×2袋」という数量表記を「20gが2つ」と考えて総量は40gであることの理解に役立ちます.
「量×量」は,面積をはじめ,多くの物理量の定義や計算に不可欠です.
そして,先ほどの図のように,「量×数」を真ん中に置くのが,かけ算の式の形としても(1文字ずつ変わっていくという点で),算数・数学として見ても,自然な構成となります.外の2つは「積」のかけ算,真ん中は「倍」のかけ算,ということでこれを「かけ算のサンドイッチモデル」と呼ぶことにします.
3. 識別の方法
かけ算の構造を持ったもの*1が,上に示した3つのうち,どれに属するのかについては,分かりやすい識別方法があります.「a×b=x」*2という等式において,
- xが,a,bのどちらとも同じ性質ならば,そのa×b=xは「数×数」です.
- xが,a,bのいずれか一方とだけ同じ性質ならば,そのa×b=xは「量×数」です.
- xが,a,bのどちらとも異なる性質ならば,そのa×b=xは「量×量」です.
「性質」というのが分かりにくければ,a,b,xが,それぞれどんな値の集合に属するのかを考えてみてください.同じ集合に属するのが,同じ性質であり,そうでなければ,異なる性質です.
本記事の「量」は,「数」に相対する概念です.しかし,「連続量」「分離量」という分類は使用しません.「20g×2袋」のうちの「2袋」は,「数」となります.*3
4. 「数×数」「量×数」「量×量」の例
上のそれぞれに属する例を一つずつ,示します.
- 机の問題:教室の机は1列に6つずつ4列ならんでいます.机はみんなでいくつありますか?
机の問題に対して,6×4=24と答えたとします.その式は,場面に合うよう机を並べてたとき,「6つ」「4つ」「24こ」となります.
それらはみな,机の数で,同じになるので,これは「数×数」です.
単位に付く「つ」や「こ」は,同じ性質かを判断するのに必ずしも使えない点に注意してください.どうしても,すべての単位を同じにしたければ,机なら「台」*4にすることもできます.
- りんごの問題:さらが 5まい あります。1さらに りんごが 3こずつ のって います。りんごは ぜんぶで 何こ あるでしょう。
こちらは,どうでしょうか.式は例えば,3×5=15です.3は,りんごの数,5は,さらの数,そして15は,りんごの数です.
といったわけで,りんごの問題は,先ほどの識別方法で「量×数」に属することになります.
補足しておくと,「3こずつ」とあるりんごの数は,整数に限る必要はなく,「2/3こずつ」などに置き換えることもできます.この意味で,量として扱うことができます.
一方,さらの数のほうは,小数・分数に替えられない*5上に,「さらが 5まい」のところを「かごが 5つ」や「5人」に置き換えても,同じようなりんごの均等分布の場面を作ることができます.したがってこちらは,数です.
- 長方形の面積:縦3cm,横7cmの長方形の面積を求めなさい.
この場合,式は3×7=21ですね.3cmと7cm,かけて出たのは21cm^2.これは「量×量」です.
5. 「数×数」「量×数」vs「量×量」
「数×数」と「量×数」と「量×量」は,先ほど書いた分類方法によって,いずれも異なるものとなります.言い換えると,3つの「かけ算の構造」あるいは「かけ算モデル」があるのです.
ですが,そのうちの2つを連合させることもできます.
「数×数」と「量×数」では成り立つけれど,「量×量」では成り立たないものを,示しましょう.「数×数」と「量×数」は,そのかけ算をたし算に置き換えたとき,かけられる数または量をそのままにすることができます.かける数に「台」や「まい」があっても,それはなくなります.あえて言うなら,「倍」に転換されます.
先ほどの机の例だと,6×4=6+6+6+6=24としたとき,そこの「6」はどれも,机の台数です.りんごの例だと,3×5=3+3+3+3+3=15ですが,6回出現する「3」はみな,りんごの数ですね.
ですが面積の場合,3×7=3+3+3+3+3+3+3=21とするとき,最初の3は「3cm」なのに対し,たし算の3は「3cm^2」と変わります(あるいは,「3cm×7cm=3cm^2×7」といった式変形を必要とします).
6. 「数×数」「量×量」vs「量×数」
今度は,「数×数」と「量×量」では不具合が起こらないけれど,「量×数」ではちょっと配慮が必要な話を,持ってきましょう.それは,交換法則です.
机の例では,6×4=24のほかに,4×6=24も,その状況を表した式になります.タテヨコに並べるというのは,そういう見方ができるということです.交換法則の式としては,6×4=4×6です.
長方形の面積も,3×7=7×3で,問題ありませんね.
りんごの問題では,「5まいのさらに3こずつのりんご」と「5こずつのりんごが3まいのさらに」で,その場面が違ってきます.ですが総数は同じです.5×3=3×5と,「=」で結べますが,左辺の状況と右辺の状況に,違った意味*6を与えることになります.
7. 場面を増やす
あとで分類に入れていくための場面をいくつか,用意しておきます.名称や問題文は,Greerによります.
- 同等のグループ:3人の子どもが4つずつミカンを持っている.全部合わせると何個になるか?
- 同等の量:3人の子どもが4.2リットルずつミカンジュースを持っている.全部合わせると何リットルになるか?
- 速さ:ボートが毎秒4.2メートルの決まった速度で進んでいる.3.3秒でどれだけ進むか?
- 単位の変換:1インチは2.54メートルである.3.1インチは何センチメートルか?
- 乗法的な比較:鉄の重さは銅の0.88倍である.ある銅のかたまりが4.2kgのとき,それと同じ大きさの鉄のかたまりは何kgか?
- 全体と部分の関係:ある大学では,80人の学生が試験を受け,上位3/5の学生を合格にした.何人が合格したか?
- 〜倍:あるゴムバンドは,元の長さが4.2メートルで,それを3.3倍まで伸ばすことができる.完全に伸ばしたら何メートルになるか?
- 物理量:ある暖房機の電力は3.3キロワットである.4.2時間使用したとき,電力量はいくらか?
8. 自分なりの分類
これまでに挙げた例が,「数×数」「量×数」「量×量」のどれになるか,自分なりに振り分けることにします.
先ほど,机の問題を「数×数」としましたが,数学と算数の区別を考慮に入れると,「数×数」は純粋な数どうしのかけ算であってほしいと,思っています.
そして,「数×数」と「量×数」には,共通の特性,すなわちたし算に置き換えたときに,かけられる数または量をそのままにすることができると,書きました.そこで,机の問題を,「量×数」に持ってくることにします.6×4=6+6+6+6=24の「6」と「4」に,違った役割を持たせよう,という考え方でもあります.
この変更を含めまして,分類は次のようになります.

Greerの分類と,一つだけ違います.それは,単位の変換を,「量×量」に入れているところです.インチをセンチメートルにするといった,物理量の変換のほか,円をドルやユーロや他の外貨といった,通貨の両替も,ここに含まれます.そして,単位の変換のかけ算「a×b=x」で出てくるa,b,xはみな異なる性質の値です.
単位の変換には他にない面白い特性があって,レートbに対して逆数b'*7に意味があります.「1ドルが何円か」の反対(乗法的な逆元)により,「1円が何ドルか」を求めることができます.そうしたとき,「x÷b=a」は「x×b'=a」と等価です.あるレートで割るのは,そのレートの逆数をかけるのと同じ*8ということです.
10. 学校教育に基づく分類
学校教育(数教協スタイルで教えているところを除く)では,次のようになります.
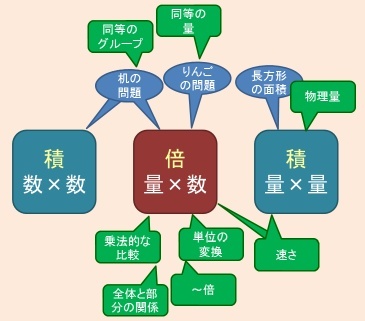
複数に属するのは,指導法が学校によってある程度違うことを意識してのことです.「机」が2つに属するのは,長方形型配列(アレイ図)を意図したものがあるからです*9.「速さ」は,割合として見れば「量×数」,比例*10として見れば「量×量」となります.
11. 批判者の世界
「かけ算には順序がない」あるいは「ここまで書いた分類なんて,どうでもいい」とお考えの方にも,こちらは分類を用意してございます.こちらです.
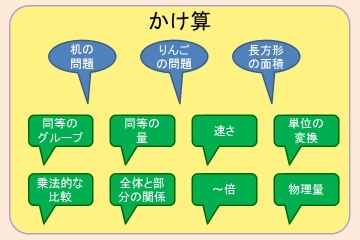
すべてが一つに収まって,気持ちいいですね.めでたしめでたし!
12. 赤いボールと青いボールのかけ算
ここで問題です.
「式が4×5になる文章題をつくりましょう」という問題に,「赤いボールが4つあります.青いボールが5つあります.かけるといくつになるでしょう」という文章題をつくった子がいました.さてあなたはどうしますか.
これには元ネタがあります.『子どものつまずきと授業づくり―わかる算数をめざして (シリーズ子どもと教育 教育をふかめる)』pp.29-34です.数値や,子どもの答えは,本記事を書くにあたり変更しています.*11
そうは言っても,「赤いボールが4つあります.青いボールが5つあります」では,かけて意味のある数量を得ることは,できませんね.
大人なら「それ,かけ算になってないよ」と言えば,おしまいです.しかし,「赤いボール」を言った子は,なぜかけ算になっていないのか,そして何がかけ算なのか---かけ算の意味---を,理解していなかったのです.
となると教育に期待したいのは,何がかけ算なのか---かけ算の意味---の指導です.どんな場面で,かけ算を使えるのか,かけ算の式から,何を読み取ればいいのか,「=答え」がない状況で,九九や筆算を使って正しい答えが出せるか,0や小数点の処理を間違えないか.そして答えの量や単位が何になるかを,きちんと推論できるのか.そういったことが含まれます.
とはいえ,それらを2年のかけ算の単元ですべて,押し込むというのは,無理な話です.1年から6年までに分かれて,かけ算を理解できるよう,学習しています.1年では「×」も九九も出てきませんが,「まとめて数える」活動が,かけ算の素地となっています.
そんなのきれい事だ,何回教えたって忘れる子,自分でやったらできない子がいるじゃないか,という反論もあることでしょう.まあ現実として,それは否定できません.私も大学で,プログラミングの指導をしていて,初期化していないポインタを参照して代入しようとするコードを頻繁に見かけ,そのたびに,講義できちんと言ったのだけどなあと,がっかりな気分になります.
ですが,できるようになってほしい子どもだけでなく,そのほんの少し周辺に,目をやることは,できないものでしょうか.
活用できそうなのは,「学び合い」です.分かっている子どもたちが,分かりたい・できるようになりたいという子どもに「教える」姿です.それでうまくいくためには,どんな知識を整備し,指導を通じて身につけさせるべきかを,考えてみてもよさそうに思います.
13. 数学的な流れ
本日提案したサンドイッチモデルに,矢印すなわち流れを載せます.

そうするとこれを,数学的な研究の流れと合わせることができます.
主に数学者が検討してきた「量の理論」は,数×数の諸性質を暗黙の了解事項とします.
次に「量の集合」を公理的に定義します.その中に,量の加法性が含まれます.といっても,3cmと3cmを足したら6cmになる,6cmは4cmと2cmに分けることができる,などが数学的に表現できるというだけのことです。A<B+B+…+B*12で表される「アルキメデスの原理」も,小学校学習指導要領 算数の第1学年に入っている「身の回りにあるものの大きさを単位として,その幾つ分かで大きさを比べること」の数式表現と言えます.
量どうしのたし算の次は,量を含むかけ算です.累加に基づき乗法を定義し,これが,「量×数」の始まりとなります.ただしこの段階では,「数」は正の整数,すなわち整数倍です.
南雲道夫の論文では,我々が「×3」などと書く,倍の概念を,線形写像で表しています.すると,「÷3」は「×1/3」と等価なので,わり算は逆写像になります.合成写像と組み合わせて,有理数(分数および小数)の乗除算が利用可能となります.実数の乗除算へと拡張するには,デデキントの切断を使います.
「量×量」に基づくかけ算やわり算は,2引数関数などを用いて実現します.田村二郎『量と数の理論』では,2つの長さをもとに面積を,また時間と距離をもとに速さを,同じ枠組みで導出しています.
ただし,この流れにおいて,「5まいのさらに3こずつのりんご」と「5こずつのりんごが3まいのさらに」とで,りんごの総数が等しくなることは,「量×数」の中だけでは導くことができません.ここは,「数×数」で知られている性質,具体的には乗法の交換法則を,利用することになります.
りんごではなく,長さの話にします.「2mの3倍」は「2m×3=1m×2×3=1m×(2×3)」,「3mの2倍」は,「3m×2=1m×3×2=1m×(3×2)」と書けます.このうち,「(2×3)」と「(3×2)」だけが「数×数」,残りのかけ算は「量×数」となるよう,演算を定義しておきます.純粋な数どうしの乗法の交換法則で2×3=3×2を使うことで,「2mの3倍」と「3mの2倍」が等しいと言えます.
14. 学校教育のかけ算指導
「かけ算には本来,順序がない」という批判については,昨日まとめました.簡単にいうと,その「本来」を,「純粋な数の世界では」の意味で使っても,机の問題に代表される「直積に基づくもの」という意味にしても,算数教育では支障のあることが,国内外の研究者・実践家らによって指摘されています.
そこで学習指導要領や,解説書・学習指導案をもとに,日本の小学校のかけ算指導について,概略を示します.
小学校では,「一つ分の大きさ」になるものと「いくつ分」になるものが明確な場面を使って,かけ算が導入されています.「量×数」なのです.
その中で,机の問題と同型となる,アレイ図に対する個数の計算を行います.このとき,「一つ分の大きさ」と「いくつ分」のペアが複数(2つまたはそれより多く)あり,授業の中では多様な式を見つけるようにしています.このようにして,「数×数」に位置される問題も,「量×数」に帰着して解くことになります.
長さなどを量とするような,「量×数」を十分に学習してから*13,4年の長方形の面積へと進みます.そこでは,アレイすなわち「数×数」と,21cm^2は,1cm^2が21個と同じ面積といった量の取り扱いを組み合わせます.
ペンキ塗りの問題から,面積は2つの長さをかけて求めるだけでなく,2つの異なる量の割合*14をもとに,かけ算やわり算で計算する場合があるのも学びます.
筆算や0,小数の処理など,純粋な数どうしのかけ算も,3年以降の各学年で見つけることができます.
そのようにして,「数×数」「量×数」「量×量」をバランスよく学習しています.
結局のところ,「量×数」を基点とする,乗法の意味の指導法が確立しているわけです.
15. おわりに
本日は,「かけ算のサンドイッチモデル」について述べ,算数の各問題の分類や,「積→倍→積」の数学また算数・数学教育における注意点を記しました.
ここで「サンドイッチ」について,いくつか関連情報を挙げておきます.かけ算の順序論争において,「サンドイッチ」は,「かけられる数と答えの単位を同じにしよう」という,かけ算の指導法として知られています.その背景についてはサンドイッチはくだらない・2012年8月バージョン(1/2)および(2/2)を,批判的な取り上げ方は「掛け算順序固定」問題対策本部 - atwiki(アットウィキ)をご覧ください.
この広く知られた意味の「サンドイッチ」と,本記事の「サンドイッチ」は,基本的には別物です.あえて関連づけるなら,「量×数」だけが,論争の「サンドイッチ」です.「サンドイッチ」が適用できないような,かけ算の場面もあることは,これまでの図から明らかです.
さらにまた違う種類の「サンドイッチ」が,『算数進度の悩みを解消!ロケット算数 小学校全学年』pp.59-62に見られます.かけ算九九について,2の段,5の段,7の段,3の段,8の段,…といった順に覚えていくという提案です.*15
*1:「USB 3.0×2」や「可憐×轟音=新連鎖。」といった,モノを含むかけ算もどきは,今回,対象外です.ところで,「USB 3.0×2」は「USB 3.0(のインタフェース)が2つ」の意味であって,「USB 6.0」とするわけにはいきませんね.
*2:もし「a×b」しか書かれていないときは,「=x」を補ってください.
*3:「20g×2袋×3箱=120g」という関係だと,「2袋×3箱(=6袋)」として見たときの「2袋」は「量」になります.「20g×2袋(=40g)」として見たとき,「2袋」が「数」となるのは,変わりません.
*4:正式には「脚」だったかな.まあ混乱のもとですが.
*5:あとで示す「同等のグループ」「同等の量」も,かける数は必ず整数となることが,他のかけ算の場面と比べた特徴となっています.
*6:東京書籍や大日本図書の教科書に見られる出題や,現行の学習指導要領を見る限り,式と場面との対応づけがより重視されています.なお,「式に表す」「式をよむ」などについては,『数学教育学研究ハンドブック』pp.83-94にまとめられています.
*7:量の逆数,と言いたいところですが,数学教育協議会主導の量の理論では,「逆内包量」という名前がついています.
*8:小数の逆数は多くの場合,無限小数になりますが,通貨の両替では,適当な範囲まで桁数をとっておけば,現実的な金額の範囲で,誤差をなくすことが可能です.
*9:長方形でない,同数の机のまとまりから,総台数を求めるとなると,「同等のグループ」です.
*10:「比例」という名称を図に入れなかったのは,比例関係にある2つの数量によって,「量×数」となることも,「量×量」に位置づけられる可能性も,あるためです.
*11:書いてから,「不備のある算数文章問題」に対する小学生と高校生の解決方略,http://hdl.handle.net/2433/57432を思い出しました.「4このポールと5このポールがあります。かけるといくつになるでしょう」という文章題に対し,小学生の多くはかけ算の式にするけれど,高校生は意味がない(不備のある文章題である)と判断しています.
*12:直観的にはこの式は,A>Bであるとしても,Bを十分な回数足し合わせれば,その和はAを超えることを意味します.
*13:ここで,前に書いた数学的な流れの欠点を一つ,挙げておきます.「量÷数」すなわち等分除は容易に実現できますが,「量÷量」になる包含除は自明ではなく,これを量の理論で表現するには,「速さ」と同じ枠組みを必要とします.
*14:割合計算のかけ算は,「量×数」です.