小数のかけ算の文章題に対して,二重数直線で解く手順を示しながら,比例関係・割合・3用法との関連を明らかにしていきます.
さっそくですが問題です.
1mの長さが80円の布を2.5m買いました。
代金はいくらですか。
これは『小学校学習指導要領解説 算数編』p.166の改題です.
解き方のGIFアニメーションは次のとおり.

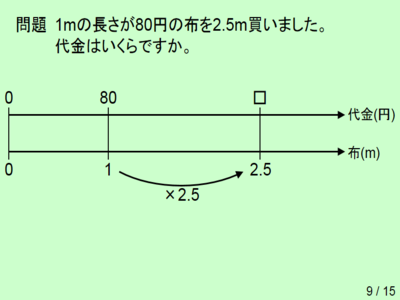
左端に縦線を入れて,その上下に「0」を書きます.小学校の算数ですので,ここより左に数量は来ません.
矢印の先ですが,上には「代金(円)」,下には「布(m)」を書いておきます.「1」があるほうを下に置くのが,慣例となっています.
この数直線の上に,値を書き込んでいきます.

「1mの長さが80円」とあるので,同じ縦位置になるように,長さの数直線上に「1」,代金の数直線上に「80」を書きます.それらを結びつける,縦の線も忘れずに.
次に「2.5m」とあるので,長さの数直線上に「2.5」を書きます.この場合は1の右に書きますが,1より小さければ,左に書くことになります*1.縦の線も,引きましょう.
「代金はいくらですか」については,2.5の上の,円の数直線上に「□」を書いておきます.これが求めたい値となります.
このとき,「1」と「□」が斜め(はすかい)の位置にあることにも,注意しておきましょう.もしそれらが同じ数直線上にあれば,第1用法を使うことになります.あるいは,縦の位置が同じであれば,それは第3用法です.第1用法・第3用法とも,わり算で求めることになります.それはさておき…
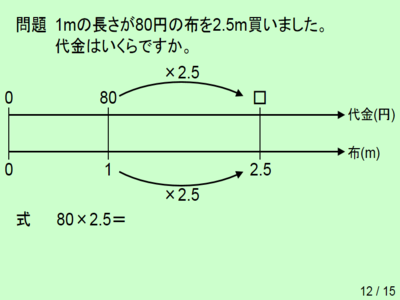
図に「かけ算の関係」を書き込むことにします.1から2.5に向けて矢印を置き,「×2.5」を添えます.
これは「1mから2.5mへと,2.5倍になった」という意味になります.最初に書いた「1」と「2.5」には,メートル(m)という単位がつきますが,「×2.5」と書いたときの「2.5」には,単位がつきません(無次元量とも言います).またこの値が「割合」と呼ばれます.この変換こそが,(ある種の)“量のかけ算”と“割合”とを結びつけるものであり*2,比例の考え方(英語ではproportional reasoningといいます)を使って問題を解く際の大事なステップとなります.
次に,「80」から「□」に向けて,同じように矢印を入れます.

そしてその矢印にも,「×2.5」を添えます.その意味は「長さが2.5倍になったら,代金は,もとの金額の2.5倍になる」です.ここが,比例の考え方(proportional reasoning)の中核をなしています.

「もとの金額」は,80円です.では「80円の2.5倍」は,いくらでしょうか.式を立てましょう.かけ算ですね.
200と出たところで,数直線の「□」に200を当てはめておき,大小関係に問題がないことも,見ておきましょう.
答えで単位を間違えると,元も子もないので…「200円」です.おしまい.

ここまでの手順を箇条書きにしておきます.
- 二重数直線を正しくかく。
- 「1」は下の数直線に
- 同じ量(長さ,金額,重さ,割合 など)は同じ数直線に
- 求めたい値に「□」
- 1と□が“はすかい”になっていれば,かけ算!
- 図を使って「何の何倍」の関係を明らかにする。
- 1から,同じ数直線のもうひとつの数に向けて矢印をかき,「×数」をそえる。
- もうひとつの数直線にも,同じように矢印と「×数」
- 式を立て,答えを求める。
- 「何を何倍したら□になる」をもとに,式を立てる。
- 暗算または筆算で,□を求める。
- 単位をつけて答えをかく。
小学校の5年で学習する,小数のかけ算・わり算の文章題*3について,次のように分類することができます.
- 第1用法か,第2用法か,第3用法か
- 割合に当たる数が,1よりも大きいか,1よりも小さいか
- 割合に当たる数が,文章題でも割合(百分率などを含む)として書かれているか,文章題では割合でない量として書かれているか
今回は「第2用法」に基づく問題であり,割合に当たる数は「1よりも大きい」のに加えて文章題では「割合でない量」として書かれています.
他のパターンの出題については,別の記事でご紹介します.
(最終更新:2014-01-11 早朝)
*1:どれだけ離して書くかというのは,この問題を解く上ではあまり重要ではありません.大小関係を間違えていないことが確認できれば十分です.
*2:Vergnaud (1983)では,「4個×15セントによって60セントが得られ60個ではないのはなぜか」と問題意識を挙げた上で,「×4」がscolar operatorに当たるとして,表に矢印を添えた図式をもとに,乗法構造の一つを解説しています.なお,「1個あたり15セント」と考え,比例(関数)関係を用いた分析も,そのすぐ後に書かれています.
*3:実はもう一つ前提があります.単一の演算(simple operationあるいはsingle operation)で求められるものという条件です.例えば,「2mの長さが80円の布を5m買いました。代金はいくらですか。」は対象外となります.田の字の解法あるいは比例式(内項と外項の積など)を知っていれば,簡単に計算できるのに,それらが採用されていないのは,なぜかというと,小数のかけ算・わり算の文章題を通じて適切に演算の決定ができ,比例の考え方を用いて式を書けるようになることが,期待されているからです.

