わさっきhb

大学（教育研究）とか ，親馬鹿とか，和歌山とか，とか，とか．

量と「×」

OoM reprise

目次

  • 1. これまで書いてきたこと
    • 分離量と連続量
    • 先人の量の認識
    • 15セントのケーキを4個
    • 3mの5倍と5mの3倍が等しいのはなぜか
    • 内包量とは
    • 足せる内包量，足せない内包量
    • 「1あたり量」とは
  • 2. 量をめぐるQ&A
    • 「一つ分の数×いくつ分＝全体の数」に交換法則を適用して「いくつ分×一つ分の数＝全体の数」としてはいけないのか?
    • 「おじゃまぷよの数×500の攻撃」は，おじゃまぷよの数を500倍にするの?

1. これまで書いてきたこと

分離量と連続量

（初出：分離量と連続量，かけ算とわり算）

小学校の算数だと多くの場合，整数が分離量に，小数と分数が連続量に対応づけられます．
本をみていきます．

(1) 分離量（離散量）と連続量
量は自然数（あるいは整数）と対応付けられる場合に「分離量」（または離散量）、実数と対応付けられる場合に「連続量」と呼ばれる。従来の科学での多くの量は連続量であるが、その近似値である測定値は離散量であり、近年コンピュータの発達とともに離散量の取り扱いの重要性が増している。
個数や人数など0を含む整数で表現できるものは「分離量」であり、長さ、時間、重さ、面積などは「連続量」である。量は正の実数（小学校においては正の有理数）に対応させることが可能であり、これによって大小・相等の比較ができる。
小学校算数科「量と測定」領域においては、長さ、面積、体積、時間、重さ、角の大きさ、速さなどの連続量、及び、メートル法の単位の仕組みを学習する。
(『小学校指導法 算数 (教科指導法シリーズ)』p.136)

簡潔で，小学校の先生向けの記述になっています．
教師でない者が読む際には，「量と測定」という領域に，注意を払うのがよいように思います．学習指導要領やその解説でも，「数と計算」「量と測定」「図形」「数量関係」という4つの領域に分けて説明されています．「算数的活動」を加えて，6学年5領域という分け方もあります．
もちろん，各領域が完全に分かれているわけではなく，学習指導要領をミニマム・エッセンシャルととらえるなら---実は2年のうちに，長さを含むたし算・ひき算・かけ算を取り入れた授業例や問題集も多く見られるのですが---，長さの測定は第2学年なのに対し，長さを含む計算は，第3学年の「数と計算」の領域に入っています．例えば「1mのねだんが85円のリボンを25ｍ買うと代金はいくらか。」「ひもを4等分した一つ分を測ったら9cmあった。はじめのひもの長さは何cmか。」といった問題です．後者の問題文は時代に応じて変化しており，はじめのひもの長さは〜指導書・解説よりで取りまとめています．
「分離」「離散」ともに，学習指導要領にもその解説にも出現しません．「連続」は，いくつか見かけますが，上の意味とは異なる使われ方です．これらの言葉が陽に出てこないのは，推測ですが，人物としては遠山啓と銀林浩，団体としては数学教育協議会が主導してきた概念・用語である点が，大きいように感じます．とはいえ，現在ではこの団体を超えて理解されていることを，いろいろな本を通じて伺い知ることができます．
算数教育では「分離量」のほうが「離散量」よりもよく使われているので，当ブログの算数教育関連エントリでもこちらを採用しています．ただし，「分離量」とは言うけれども「分離値」「分離的」「分離化」とはあまり書かれず，「離散値」「離散的」「離散化」となる，という点にも注意をしておきたいところです．

また別の本をみます．

[1] 分離量
みかんの個数，児童の人数などのように，それを細かく分けていくと，ある単位以上に細かく分割できない，おのずから最小単位が決まってくる。このように最小単位の決まっている量を分離量（離散量）という。
したがって，その分離量が幾つあるかを調べれば，その量の大きさが決まる。その量の大きさの決定は「数える」ことによってなされる。このことから，分離量は物の個数を表す量のことであり，自然数（1，2，3，…）で表される。
(略)
[2] 連続量
コップの中の水は，一つにつながっており，いくら細かく分割しても水がある状態に変わりがないし，しかも分割したものを一つのコップに入れて合わせると元どおりのつながった水になり，全体の体積に変化を生じない。このような量は，個体をなしておらず，数えることのできないもので，連続量という。
連続量は，分離量と違って最小単位がおのずから決まっていない。したがって，連続量の大きさは，人為的に単位を決めて，測定という操作によって，その幾つ分であるかを調べなければならない。
小数や分数は，その連続量の測定においてはしたの部分の処理に伴って生じた数とも考えられる。したがって，小数・分数，さらに実数の概念形成はこの連続量が基礎となる。小学校では実数のうちの小数や分数で連続量を表す。
（『算数教育指導用語辞典』p.76）

ここで目を引くのは，「最小単位」です．最小単位が決まっているなら分離量，そうでないなら連続量，というわけです．
このあたりのことを，数学を使ってきちんと論じているのは，『量の世界―構造主義的分析 (1975年) (教育文庫〈8〉)』pp.32-43です．要約すると，(1)量の全体Gがアルキメデス的全順序群をなす*1こと，(2) Gの正の要素の中で最小元があれば，Gは整数群Zと同型であること（すなわち分離量），(3) そのような最小元がなければ，Gは実数群Rの中に忠実に埋め込まれること（すなわち連続量），となります．
なお，実数と小数・分数の関係について，一歩踏み込んだ見方をしている点も，留意しておきたいところです．

「分離量」「連続量」の違いを確認したところで，注意したい量の例を2種類，取り上げます．
一つは，小数・分数で表されるものの中にも，離散量とみなせる量がある点です．
例えば円形のピザを等しい大きさに切ることにします．いくつに分けるかが決まっていないのなら，最小単位がないので連続量，ですが，3つに切って（複数の同じ大きさのピザも同様に切って）いくつかを持てば，それが何切れあるかというのは明らかに分離量ですし，合わせると1枚のピザのいくつ分（何倍）になるかというのも，最小単位があるわけですから，分離量とみなせるのです．
小数で表すものには，通貨があります．といっても日本の日常生活では，1円単位が当たり前です．もちろん分離量です．ドルやユーロでは，レシートを見れば分かるように，1ドルまたは1ユーロを表示上の単位として，それ未満の値は「セント」となります．1セント未満は無視されます．日常生活の支払い，お勘定という点で見れば，最小単位は1セント，すなわち0.01ドルまたはユーロ，となるわけです．これは，小数を含んでも分離量になる事例です．
どうやら「金額」は，計算で一時的に分数だとか循環小数だとかが必要になるとしても，最終的には分離量で表すことが想定されている，と考えるのが良さそうです．
次は反対に，連続量になるものを取り上げましょう．
「人」という単位で表されるものは，本当に常に分離量なのかというと，答えは「連続量になり得る．それも小学校の算数の範囲で」です．具体的には「平均」です．
あるクラスで，9月3日月曜日は2人休み，4日火曜日は3人休み，…と欠席人数を数え，1週間でも1か月でも1年でもいいのですが，平均の欠席者数を求めたら，おそらくは整数値になってくれません．その際，わる数（または分母）にあたる出席日数は固定ではないため，最小単位がないことになります．といったわけで，「人」という単位であっても，またどのような分離量をもとにしても，平均値を求めることで，連続量になり得るのです．
先ほどの本では，この取り扱いについて，次のように書いています．

回数が等しくない場合は，平均による比較となる。この場合，前出の例のように，17÷5＝3.4(人)，20÷6＝3.3(人)などと，人数が小数で表されることに疑問を覚える児童がでてくるであろう。人数を数えるときは整数を用いるが，人数の平均を表すには，3.4人のように小数で表すことがあることを十分に理解させておくことが必要である。これにより，平均値を比較したり，計算に用いたりできるわけである。
（『算数教育指導用語辞典』p.247）

先人の量の認識

（初出：次のステップ）

洋の東西を問わず…というのは言い過ぎなので，我々がアクセス可能な範囲で，先達が「量」をどのように認識してきたかについては，「見取図」が作られています．

(p.27)
もちろんこの図が完成形，ではありません．というのも，この図には高木貞治の名前が見当たりませんが，おそらく著者は，現在なら文庫本で入手可能な『新式算術講義 (ちくま学芸文庫)』をはじめ，高木の著書にアクセスできなかったのでしょう．
なお，高木貞治については，以下の文献で，幅広い年代の著書を通じた検討がなされています．そこでも，主要な役割を演じているのは，「量」です．

15セントのケーキを4個

（初出：次のステップ，Vergnaudと銀林氏の「かけ算の意味」）

「量」と算数・数学教育の中で，もう一つ思い浮かぶのは，Vergnaudの文献です．

  • Vergnaud, G. (1983). Multiplicative Structures, In Lesh, R. and Landau, M. (Eds.), Acquisition of mathematics concepts and processes, Academic Press, pp.127-174. isbn:012444220X

そこには，「a×b＝x」の構造を示す，2種類の図が載っています(p.130)．


その前のページには，"two measure-spaces M1 and M2"と書かれています．measure-spaceは「量空間」と訳すのがよく，『算数・数学科重要用語300の基礎知識』(p.187)においても，この語が使われています．なお，Vergnaudは"Multiplicative Structures"と題して，内容の異なる文章を，1988年にも書いています．関心のある人は，5まい×3こ/まい，トランプ配りと，うまくやっていくをどうぞ．
上の図に話を戻しまして，それぞれの考え方を，直訳ではなく自分なりに解きほぐしていくことにします．
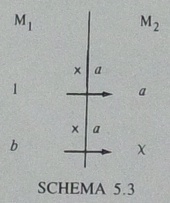
まず，「1個15セントのケーキを4個買います．いくらになりますか」という問題を考えます．aを15セント，bを4個とします．xは60セントであって，60個ではありませんね．SCHEMA 5.2, 同5.3とも，M1はケーキの個数の量空間，M2は金額の量空間です．
SCHEMA 5.2の考え方では，M1で1個から4個になるのを「×b」とします．同じ量空間における「b倍」を，M2へ適用することで，a＝15セントの「4倍」がx＝60セントになるわけです．
このとき，「×b」のbは，もはや「4個」ではありません．あえて量という言葉を使うなら，無次元量です．
SCHEMA 5.3は，横に見る関係*2といえます．1個だと15セント，という関係を「×a」で表します．そうすると，4個だと，「×15」とするので60セントです．
ちょっと注意したいのは，この場面での「×15」は，数だけ見れば15倍ですが，実際には，M1という量空間からM2という量空間へ変換しています．あるいは，「×a」が，M1とM2という2つの異なる量空間の仲立ちをしている，と考えることもできます．
このとき，「×a」のaは，これまた「15セント」ではなく，「15セント/個」とするほうが，より適切でしょう．言葉にすると，「1個（あたり）15セント」です．
量空間は，数学的に定義しているわけではなく，同じ性質の集まりという程度なのでしょう．その一方で，数学的な取り扱いでの「量」だと，連続量が対象とせざるを得ないところ，Vergnaudの議論では，ケーキの数や金額など，分離量も視野に入れています．
何に依拠するにしても，一長一短があるといったところで．

3mの5倍と5mの3倍が等しいのはなぜか

（初出：1970年代の乗法構造(2)―量と数の理論，比の乗法）

「3mの5倍」は15mです．「5mの3倍」も15mです．等しいことを，数学の道具立てでどのように考えればいいでしょうか．
田村二郎『量と数の理論 (1978年)』にその答えがあります．
「量×数」を適切に定義すれば，3mの5倍は3m×5＝（m×3）×5＝m×（3×5）＝m×15＝15m，また同様に5mの3倍は5m×3＝（m×5）×3＝m×（5×3）＝15mとできます。
この中で，「（3×5）」と「（5×3）」のみが数×数（交換法則が利用可能），残りのかけ算は量×数（交換法則は使えない）です。それと，カッコの位置変更は，結合法則ではなく，「量×数」の定義によります。『量と数の理論』では，「量×量」についても記されています。

1970年代に書かれ，かけ算を含む「量の理論」が整理されたものとして，以下の書籍・論文があります．

当ブログでは英文から学ぶ，数学者による「かけ算の順序」で見てきています．それと懐古趣味。 - 担当授業のこととか，なんかそういった話題。が読みやすいガイドとなっています．

量に対するかけ算と，線形性，そして量の構造については，『線型代数』(pp.44-45)で次のとおり明快に記されていました．

(4.1.4) 実数の発生学
量の空間そのものの抽象化として実数体があらわれるのではない．
実在とのつながりを考えると，まず同種類の量の空間Xが意識される．Xにおいては加法が意味をもつが，乗法は，例えば 3秒×4秒，3cm×4cmのように，少なくともXの中の積としては意味をもたない．しかし，Xの二つの元の比を考えると，この比はXに作用する．この作用（倍概念）の合成として，比の乗法が定義される．こうして一つの量の空間Xに対して倍変換の体End(X)が作られ，XはEnd(X)上の線形空間となる．さまざまな量の空間に対するEnd(X)の本質的な同一性を意識するとき，実数体Rが生まれる．
もちろん，今日の数学では普遍的な体Rから出発して公理的に線型空間を定義するが，実際には，量の構造についての認識の（歴史的，心理的な）過程は，まず量の1次元線型空間が，そしてその係数体の抽象としての実数体が，という順序になっている．“量の理論”にとって線形代数がその自然な枠組となるのは，以上のような理由からいっても当然のことである．“多次元の量”の理論が線型代数なのではなく，“1次元の量”から線型代数は始まる．

今回挙げた書籍や論文から，輪郭をつかむことのできる「乗法構造」は，量の空間における比の乗法です．算数教育と関連づけようとするなら，「Xの二つの元の比」は比の第一用法，「比の乗法」は第二用法に対応します．
ですが，かけ算の式の書き方は，文献によって異なります．『量と数の理論』では，量Uのn倍をU×nと表記しているのに対し，『線型代数』には「3×1.5袋＝4.5袋」や「3x＝(4.5袋, 6箱, 9ピン, 6カン)」といった式が見られます．xの係数3，あるいは「3×」が，スカラー倍に対応しています．
なお，nxあるいはn・xと書き，xが被乗数に対応する量，係数nが乗数に対応する無次元量として，「n倍のx」を表す書式もよく見られます（数学者による「かけ算の順序」）．その場合，x・nやxnとは書かれません．またVergnaud (1988)にある「Connie wants to buy 4 plastic cars. They cost 5 dollars each. How much does she have to pay?（コニーは4個のおもちゃの車を買いたい．1個は5ドルする．いくら払わないといけないか?）」に対する答え「4・5＝20」「5・4＝20」も，この書式になっていて，「・」の左が乗数です．4・5と5・4とでは，答え（総額）は同じでも解釈が異なっています．

内包量とは

（初出：内包量とは）

「内包量とは何か?」「内包量は足せないの?」などの問題意識をもとに，手元の本を読み直しました．
まずは：

  • 遠山啓: 「内包量とはどんなものか」, 算数教育, 1960年11月号.

『遠山啓著作集数学教育論シリーズ 5 量とはなにか 1 (1978年)』(pp.104-112)に収録されています．以下のページ番号も，この本からです．引用にあたり，リットルと度（温度）の記号を「L」「℃」に置き換えています．

初等教育でとりあつかう量は，なにかの物体もしくは物質の一側面を表わす指標なのである。そして，物体もしくは物質そのものではないのである。3メートルの棒，高さ3メートルの家は，物体もしくは物質として存在するが，3メートルそのものは存在しない。つまり，量の背後にはかならず物体もしくは物質が存在しているのである。背後にある物体もしくは物質と，その一表現である量とがどのようにかかわりあうかにしたがって外延量と内包量との区別が生じてくる。
ところで，物体もしくは物質に対するもっとも基本的な操作は合併である。たとえば，二つのバケツのなかにはいっている水をあわせて一つにするような操作が，この合併という操作である。この合併に対して加法的なのが外延量であり，そうでないのが内包量である。
たとえば，二つのバケツのなかにはいっている水の体積がそれぞれ3Lと5Lだとすれば，あわせた水の体積は3L＋5L＝8Lになるのである。このように体積では合併から加法という演算が決定されるのである。このような性質が加法的といわれるもので，このような加法性をもつ量を外延量というのである。(略) そういう意味で物理学の三つの基本的な量である長さ(L)，時間(T)，質量(M)は外延量であるといえよう。
これに対して，合併が加法を意味しないような量も存在する。密度・濃度・温度・速度・単価などがそうである。20℃の水と30℃の水をあわせてかきまぜても，50℃にはならないで，20℃と30℃とのあいだのある値をとるだろう。つまり，合併から加法がでてこないのである。このように加法的でない量が内包量である。(略)
(pp.107-108)

単純に足せる足せないではなく，「合併（あわせて一つにするような操作）」に対して，足せる（加法的な）量が外延量，足せない（加法的でない）量が内包量，と記されています．
『新版 水道方式入門〈小数・分数編〉 (現代教育101選)』(p.27)（http://books.google.co.jp/books/about/%E6%B0%B4%E9%81%93%E6%96%B9%E5%BC%8F%E5%85%A5%E9%96%80.html?id=CE4LY17SPeoC&redir_esc=yの「書籍のプレビュー」から読むこともできます．）では，速度について，2台を連結しても，足し算した速度にならない（小島順『線型代数』(p.139)にも「上り坂を進む列車を機関車2台で引っ張ると，速度が1台のときの2倍になるかどうか，という問い（答：一概には何ともいえない）とは何の関係もない」とあります）けれど，反対方向に進む2つの乗り物の相対速度（1時間あたりの，両者の間の距離）は，足し算で求められ，これは合併による足し算ではないことが，指摘されています．

次に：

  • Schwartz, J. L.: "Intensive quantity and referent transforming arithmetic operations", Number concepts and operations in the middle grades, National Counsil of Teachers of Mathematics. pp.41-52 (1988). isbn:0873532651

文献全体の概略については内包量×外延量，I×Eをご覧ください．以下，intensive quantity（内包量）とは何かについて，主要部を書き出し，私訳を添えました．

I have argued elsewhere (Schwartz, 1976, 1987) that the proper understanding of the use of multiplication and division in modeling our surround depends on the introduction of a type of quantity that is ordinarily not either counted or measured directly: "intensive" quantity. To understand the need for intensive quantity, consider the problem of putting together amounts of coffee beans (assumed for our purpose to be a continuous quantity). Suppose we have a pile of coffee beans characterized by the following three adjectival quantities:
(5.0, lb, weight of coffee)
(15.00, $, cost of coffee)
(3.00, $/lb, price/lb of coffee)
If we have two such piles of coffee beans and coalesce them, it is clear that the appropriate mode of composing the quantities describing the weight and the cost of the coffee differs from the appropriate mode of composing the quantity that describes the price per pound.
The fact that the mode of composition of the price per pound quantity is different from the others is a clue. The price per pound quantity is a different sort of descriptor of the coffee. Whereas the first two quantities describe the entire pile of coffee beans, the price per pound quantity can describe not only the entire pile of coffee beans but also a single coffee bean or a freight car full of them. It is a descriptor of a "quality" of the coffee and not of the amount of coffee. It is called an intensive quantity. For the most part, mathematical intensive quantities can be recognized by the fact that their unit measures almost always contain the word "per." (It should be pointed that an intensive quantity need not have the word "per" appear explicitly in its unit measure. Often it is implicit as in the case of the "knot" or nautical mile per hour, for example. Another interesting case of an intensive quantity is temperature. A degree is a measure of the average kinetic energy per particle in a material. The nonobvious intensity gives rise to the substantial difficulty that many adults as well as students have in distinguishing heat and temperature.)
（私訳：以前にも述べたとおり(Schwartz, 1976, 1987)，我々の身の回りで使われるかけ算やわり算のことを適切に理解するには，通常は直接的に数えたり測ったりしないような量，すなわち「内包」量をどのように導入するかが重要となっている．内包量の必要性を理解するため，コーヒー豆のブレンドを考えることにしよう（ここでコーヒー豆は連続量であると仮定する）．山積みのコーヒー豆に対し，次のような量を見出したとする．
(5.0, ポンド, コーヒーの重量)
(15.00, ドル, コーヒーの価格)
(3.00, ドル/ポンド, コーヒーのポンドあたりの価格)
2種類の山積みのコーヒー豆を混ぜたとき，重さに関する量の合成，価格に関する量の合成と，ポンドあたりの価格に関する量の合成との間に，明らかに違いがある．
ポンドあたりの価格の量の合成が，重さや価格の場合と異なるという事実は，内包量を理解するための手がかりとなる．ポンドあたりの価格という量は，対象とするコーヒーについて，異なる種類の表現を与える．重さや価格は，コーヒー豆の総量に対する特徴を示しているのに対して，ポンドあたりの価格は，コーヒー豆の総量だけでなく，1粒のコーヒーの豆や貨車1台分のコーヒー豆に対する情報も示すことができる．それはコーヒーの量（総量）ではなく「質」に対する特徴を示すこととなる．これが内包量である．算数・数学に現れる内包量では，たいてい，その単位に「あたり」が入っている．（しかし次のことも指摘しておかねばならない．すなわち，内包量の単位に「あたり」が明示されてなくてもよい．例えば，船の1時間あたりの速さを表す「ノット」には見当たらない．内包量となるまた別の興味深い例として，温度がある．温度は，物質の粒子あたりの平均運動エネルギーで測られる．温度が自明でない内包量であることは，生徒だけでなく大人も，熱と温度の区別を実質的に困難にしている．）
(pp.42-43)

途中の「coalesce」について，辞書を引くと「合体する」という意味があります．要は合併ですので，この単語を含む文は，内包量は加法性を持たないという主張になっています．
加法性を持たないことを，数式を使って，次のように考えればいいのでしょうか：重さm1，m2のコーヒー豆の価格がそれぞれp1，p2のとき，単価はp1/m1，p2/m2と表せます．それらのコーヒー豆を一つの袋に入れてしまうと，重さはm1＋m2，価格もp1＋p2となりますが，そのの際の単価(p1＋p2)/(m1＋m2)は，それぞれの単価の和にはなりません（式で表すと，(p1＋p2)/(m1＋m2)≠p1/m1＋p2/m2）．
温度もまた内包量となる理由で，「the average kinetic energy per particle in a material」（物体の粒子あたりの平均運動エネルギー）を挙げていますが，数学教育協議会の人々の著書では見たことのない解釈でした．

ところで，合併でない操作に対して，足せる場合があるのには注意したいところです．典型的なのは，すでに述べたとおり，反対方向に等速で進む場合の相対速度です．あと一つは，増加（添加）による操作，例えば20℃の水に湯を注いで30℃にする（20℃＋10℃＝30℃）ようなものが挙げられます．

足せる内包量，足せない内包量

（初出：足せる内包量，足せない内包量）

さっそくですが問題です．

何も のって いない 青い さらが 5まい あります。
1さらに りんごを 3こずつ のせます。
りんごは ぜんぶで 何こ あるでしょう。

答えは「15こ」です．パー書きの量を使って，「3こ/さら×5さら＝15こ」という式で表せます．
続けてですが問題です．

1さらに みかんを 5こずつ のせます。
くだものは ぜんぶで 何こ あるでしょう。

りんごを乗せてからみかんを乗せる，という展開です．答えは「40こ」です．式ですが，りんごは「3こ/さら×5さら＝15こ」，みかんは「5こ/さら×5さら＝25こ」，たし算して，「15こ＋25こ＝40こ」となります．小学校2年の範囲を超えますが，「3こ/さら×5さら＋5こ/さら×5さら＝15こ＋25こ＝40こ」と書くこともできます．
別の求め方もあります．1さらあたりで見ると，何もない状態から，りんごを3個ずつ，そしてみかんを5個ずつ乗せたのですから，「3こ/さら＋5こ/さら＝8こ/さら」となります．そしてそれが5皿ですから，「8こ/さら×5さら＝40こ」です．一つの式で表すと，「（3こ/さら＋5こ/さら）×5さら＝8こ/さら×5さら＝40こ」です．
なのですが，このように書いて，本当にいいのでしょうか?
「/」を単位に含む量は，内包量と呼ばれます．そして内包量は加法性を持たない，すなわち「足せない」量なのも，広く知られています．
ですが上の問題では，「3こ/さら＋5こ/さら＝8こ/さら」と，足すことができました．りんごやみかんの長方形配置や，かけわり図で表しても，足せるのが確認できます．
どんなときに，そのまま足すことができて，どんなときには，そのまま足すわけにいかないかを，考えることにしましょう．新たにですが問題です．

赤い さらが 5まい あります。1さらに りんごが 3こずつ のっています。
白い さらも 5まい あります。1さらに みかんが 5こずつ のっています。
くだものは ぜんぶで 何こ あるでしょう。

こうすると，「3こ/さら×5さら＋5こ/さら×5さら＝15こ＋25こ＝40こ」は問題ありませんが，「（3こ/さら＋5こ/さら）×5さら＝8こ/さら×5さら＝40こ」には抵抗があります．「3こ/さら＋5こ/さら＝8こ/さら」が，この場面には見られません．
総数で言うと，りんごは15個，みかんは25個ですので，果物は40個です．入れ物のほうは，赤い皿が5枚と白い皿が5枚で，合計10枚です．
もし，果物の数は増えも減りもせず，どの皿にも同じ個数の果物を乗せるとするなら，「40こ÷10さら＝4こ/さら」となります．例えば，みかんを移動させれば，りんご3個ずつとみかん1個ずつという皿が5枚，みかん4個ずつという皿が5枚，ですので，「さらが 10まい あります。1さらに くだものが 4つずつ のっています」という状況（式に表すと「4こ/さら×10さら＝40こ」）をつくることができます．
皿が10枚ある状況から，「3こ/さら＋5こ/さら＝8こ/さら」を得るためには…冒頭で2つに分けて書いた，青い皿の問題と結びつけてみましょう．手続きは，次のようになります．

  1. りんごが3個ずつ乗った赤い皿を5枚，用意します．赤い皿には1から5までの番号を振っておきます．
  2. みかんが5個ずつ乗った白い皿を5枚，用意します．白い皿にも1から5までの番号を振っておきます．
  3. 何も乗っていない青い皿を5枚，用意します．青い皿にも1から5までの番号を振ってきます．
  4. 番号i（i＝1,2,3,4,5）の赤い皿のりんごを，番号iの青い皿に移し替えます．
  5. 番号i（i＝1,2,3,4,5）の白い皿のみかんを，番号iの青い皿に移し替えます．

移し替える前の状態は，「3こ/さら×5さら＋5こ/さら×5さら＝15こ＋25こ＝40こ」で表されます．また移し替えた後の青い皿に着目すると，「（3こ/さら＋5こ/さら）×5さら＝8こ/さら×5さら＝40こ」と書けます．
青い皿の果物について，赤い皿と白い皿へ同数になるよう振り分け，何も乗らなくなった青い皿を取り除くと，「40こ÷10さら＝4こ/さら」も得られます．

さて，足せる内包量，足せない内包量は，次のように定式化できます．
内包量は，2つの外延量の商であるという考え方から出発します．そして，内包量を持つ2つの対象a1およびa2が，何らかの方法で合併でき，合併された対象a3に至るものとします．
ここで，a1，a2，a3の持つ内包量をそれぞれI1，I2，I3と表記し，次のように商として書くことにします．
I1＝E11÷E12
I2＝E21÷E22
I3＝E31÷E32
E11とE21とE31はある量空間に属する外延量で，内包量の被除数と呼ぶことにします．E12とE22とE32は別の量空間に属する外延量で，内包量の除数と呼びます．量どうしのわり算については，話を簡単にするため，I*，E**はいずれも実数（そしてE*2は0でない）と仮定しておきます．
こうしたとき，I3＝I1＋I2を満たすときに「足せる内包量」，I3≠I1＋I2のときに「足せない内包量」と定義します．次の2つの等式をともに満たすとき，足せない内包量となります．
E11＋E21＝E31
E12＋E22＝E32
これと先ほどのI1，I2，I3の式とを結びつけると，2つの内包量の被除数どうし，除数どうしを足すことで，合併後の内包量の分子と分母が求められることを意味します．式は次のとおりです．
I3＝E31÷E32＝（E11＋E21）÷（E12＋E22）
ここに実用的な仮定としてE11,E12,E21,E22＞0（ゼロやマイナスの量を対象としない）を置けば，
I1＋I2＞I3
となります．実際，I1＋I2−I3＝（E12・E12・E21＋E11・E22・E22）÷（E12・E12・E22＋E12・E22・E22）＞0です．
それに対して，次の2つの等式をともに満たすときには，足せる内包量となります．
E11＋E21＝E31
E12＝E22＝E32
内包量の被除数どうしは足しますが，除数は同等という場合です．このとき，次にようにして，合併後の内包量は，合併前の2つの内包量の和となることが確認できます．
I1＋I2＝E11÷E12＋E21÷E22＝E11÷E32＋E21÷E32＝（E11＋E21）÷E32＝E31÷E32＝I3

事例を見ていきましょう．青い皿にりんごやみかんを乗せて，内包量のたし算ができたのは，5枚の青い皿がE12＝E22＝E32の役割を果たしていたからです．それに対し，「40こ÷10さら＝4こ/さら」のほうは，「（15こ＋25こ）÷（5さら＋5さら）」と書くことができ，足せないほうの条件に当てはまるのでした．割り切れるように，3種類の皿の枚数そして果物の個数を設定しましたが，個数を変えれば割り切れるとは限らず，赤い皿と白い皿の枚数が異なると，平均で求めるわけにもいかなくなります．
相対速度も，共通する時間がE12＝E22＝E32に対応し，足せる内包量となります．http://d.hatena.ne.jp/takehikom/20140330/1396126613で書いたコーヒーのブレンドの件は，コーヒー豆の価格についてE11＋E21＝E31，重量についてE12＋E22＝E32となり，足せない内包量です．食塩水を混ぜたり，30℃と40℃のお湯を混ぜたりといった，濃度や温度を「足せない」場面についても，E12＋E22＝E32となる量を見つけることができます．
人口密度について，「和歌山県の男性の人口密度と女性の人口密度」は足せますが（順序数どうしの足し算，アフィン空間，量再考），「和歌山県の人口密度と茨城県の人口密度」を単純に足すと，おかしくなります（https://twitter.com/tetragon1/status/450487065348558848）．これもまた，E12，E22，E32に対応する，県の面積が共通か異なるかによって，説明できます．
「内包量の和」については，過去に矢野寛が検討したというのを把握しています（温度はたし算・引き算できないか(1) 『ことば・その周辺』）が，当該文献は読んでいません．

「1あたり量」とは

本から，記事を紹介します．

小数の乗法をタイルで考えるという教育実践を紹介し，それは不自然であると論じています．タイルは十進位取り記数法の理解には良いが，小数どうしのかけ算で利用するのには到底納得がいかない，とのことです．
「小数の乗法」について，次の2つを対象としています．

  • 小数第1位までの小数どうしの積で発生し得る，小数第2位の数は何を意味するのか：「1mの重さが2.1gの針金がある。3.2mでは，重さは何gか」(p.94)
  • 1より小さい数をかけると，積はかけられる数より小さくなるのはなぜか：「1mの重さが3.2gの針金があります。0.4gでは何gになりますか」(pp.94-95)

「到底納得がいかない」は，次の箇所がもっとも顕著です．

そもそも，「2.1g/m×3.2m」の計算のタイル図で，「たて2.1g」「よこ3.2m」の長方形が描かれるが，筆者にはこれがそもそも理解不能である。「たてが重さ，よこが長さ」というものはなんなのだ。これはそもそもどういう具体的なものの操作に対応しているのか，まったくわからない。
(p.102)

「わからない」という著者の認識は，それより前にも現れています．

(略)ここで，彼らにとって「1あたり量」なる概念について，少なくとも「タイルにもとづいて考える」ことはまったく役立っていなかった，ということも明らかである。かれらにとって「1あたり量」というのは，「0.1mの重さ」として理解されているのである（実際，筆者自身，小学校時代に，「1あたり量」という謎めいた言葉の意味がまったくわからず，この言葉が出るたびに，ともかく「もうダメだ，ついていけない」という思いにかられたことを思い出す）。
(p.98)

文章全体を通して，見直すと，前半の授業の紹介では，タイル図を多用し，かけ算をいわば2次元のもの，そして「積」に基づいていることが読み取れます．後半の授業の提案から，著者はかけ算を1次元的に，すなわち「倍」で考えるべきだという主張を持っていることも，見えてきます．
数学教育協議会（数教協）主導の面積図において，「1あたり量とは何か」が記されている一節と図を，引用します．

ここで，教師が「それじゃあ，1あたり量はどれ?」と問うと，Nさんは図2の斜線部分アを指した．これに対し，だれからも反論が出なかったので，教師は「こうじゃないかなあ」と言って，図3を描き，1あたり量というのはこの全体の斜線部分イであることを示したが，「理解は得られなかった」という。

(p.95)

たしかに，イは「1mあたり3.2g」を表すものになっています．「時速60km」という速さの表記とも，関連します．
しかし私としては，この図2，図3の両方に，1あたり量があるように思います．というのも図2の「3.2g」を「3.2g/m」に書き換えれば，これが1あたり量になります．
面積図の高さを，パー書きの量で表したものが，1あたり量です．パー書きにすることで，縦×横で求められる（それぞれの面積図の）長方形の面積が，“量の積”となることにも対応づけられます．
p.102の件では，「たて2.1g」ではなく「たて2.1g/m」と見ればよいのです．縦の長さと面積とで，混同することも防ぐことができます．そしてSchwartz (1988)から書き出した「the price per pound quantity can describe not only the entire pile of coffee beans but also a single coffee bean or a freight car full of them （ポンドあたりの価格は，コーヒー豆の総量だけでなく，1粒のコーヒーの豆や貨車1台分のコーヒー豆に対する情報も示すことができる）」も，その見方で説明できるわけです．
このように解釈できるものの，小数のかけ算をタイル図で表す指導法には，実は賛同できません．というのも，「集まった小学生100人のうち40%が女子でした。女子の人数は何人ですか」といった，割合の場面で，面積図を作ろうとすると，縦の長さと面積が同種の量となってしまうからです．

2. 量をめぐるQ&A

Q: 「一つ分の数×いくつ分＝全体の数」に交換法則を適用して「いくつ分×一つ分の数＝全体の数」としてはいけないのか?

数学においては，より正確には，高木貞治・南雲道夫・田村二郎らが書いてきた「量の理論」では，そういった考え方による「いくつ分×一つ分の数」に相当する式が見当たりません．
理論の構築や論証にあたっては，必要かつ十分な構文を定義しておけばよいというわけです．その構文や，書籍・論文に現れる式を見た現在の我々が，「（彼らの書いた文章にも）かけ算にには順序がある」と解釈できるという次第です．
なお，『新式算術講義』でAのn倍を表すのにnAと書いているのを見つけて，これを「いくつ分×一つ分の数」と解釈するのには，やや無理があります．累加による乗法の定義（a×1＝a，a×b＝a＋a＋a＋…＋a (p.26)）と見比べると，乗算記号に「×」を用いた場合には，その左が被乗数，右が乗数ですが，「・」を用いた場合（Nagumo, 1977）や，乗算記号なく連接した場合には，その右側が被乗数に対応する量，左側がその係数そして乗数に対応する数，となっています．
この構文上の違いについて，もっとも明快に記しているのは，田村二郎『量と数の理論』の以下の箇所です(pp.17-18)．

長さAの2倍というのは，
A＋A
のことである．この長さを2AまたはA×2で表す．
同じようにして，
A＋A＋A
をAの3倍といい，3AまたはA×3で表す．
数1を例外としないために，Aの1倍はAであると決めておく：
1A＝A×1＝A
一般に，任意の自然数nに対して，長さAのn倍が定められる；それは‘n個のAの和’
A＋A＋……＋A
であり，nAまたはA×nで表される．

それはそれとして，算数（教科書，学習指導案，学力調査問題）において，「一つ分の数×いくつ分＝全体の数」に交換法則を適用して「いくつ分×一つ分の数＝全体の数」としてよいとする例は見たことがありません．「3人に5個ずつ」と「5人に3個ずつ」のいずれも，3×5でも5×3でもよいことを意味し，「式の表現」「式の読み」を重視する昨今の算数教育の流れに合わないように感じています．

Q: 「おじゃまぷよの数×500の攻撃」は，おじゃまぷよの数を500倍にするの?

（初出：ぷよぷよクエストのスキル攻撃〜おじゃまぷよの数×500）

ぷよぷよクエストで，あるボス敵が「おじゃまぷよの数×500の全体攻撃」を行ってきます．フィールドにおじゃまぷよが1個あれば500，4個あれば2000のダメージを，画面に出ている各キャラが受けることになります．ですので，おじゃまぷよの数が500倍では，ありませんね．
「おじゃまぷよの数×500」によるかけ算の結果は，（500倍の個数になった）おじゃまぷよではなく，攻撃のポイント，すなわちダメージなのです．
これは，Vergnaudの「M1という量空間からM2という量空間へ変換」を使って確認することができます．M1を「おじゃまぷよの数」空間，M2を「ダメージ」空間とし，以下の表のようにすればいいのです．

実は，「相手全体にこのカードの「こうげき」×4の属性攻撃」（シグのスキル「ラピスラズリ」）も，「×4」が，「こうげき」空間から「ダメージ」空間への変換をしていると見ることができます．
テレビを見ていても，このように，「×」の左の数量と，明示されていない積について，単位が異なる（所属する量空間が異なる）ような表記が出現することがあります．
その種の"referent transforming composition"や，「量空間」といった概念についてを，小学校の算数で扱うのは困難なように思います．自分自身は，子どもが関心・疑問を持つようになったら，話そうと思っていますが．

*1:「任意の量aおよびc（ともにGの要素）に対して，a＜ncとなる自然数nが存在する」という，アルキメデスの公理（の量への適用）が含まれています．

*2:比例を含む2つの数量の関係は，2行任意列の表を作るのが一般的です．その際，行ごとに同じ種類の情報，すなわち同じ量空間の要素を書きます．そうすると，「縦に見る関係」として，考えることができます．