いきなりですが問題です.
小中学校で実施されてきた組体操の技のうち,7段の人間ピラミッドが,55人で構成されているのはどうしてでしょうか.
「どうして」というのは,「なぜ(why)」の意味合いも含まれますが,むしろ「どのようにして(how)」です.どの段に何人が並び,上下関係(荷重をかける・荷重がかかる関係)がどのようになることで,7段の人間ピラミッドを構成するのか,本記事にて整理してみます.
対象は三角錐型です.安全性については,おしまいに少しだけ取り上げることとし,主な関心は,段数を変えても対応できる「構成法」を確立することにあります.
7段を構成するための人数とその手順について,本を1冊,挙げよというなら,次の本で決まりです.

- 作者: 根本正雄
- 出版社/メーカー: 明治図書出版
- 発売日: 2011/12/01
- メディア: 単行本
- クリック: 1回
- この商品を含むブログを見る
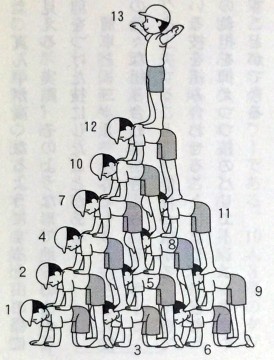
ただ,このイラストから「上下」と「前後」の配置は分かりますが,「左右」の配置,すなわち1から12までのそれぞれに何人,並んでいるかは読み取れません.
それは次のページ(p.145)に表されています.
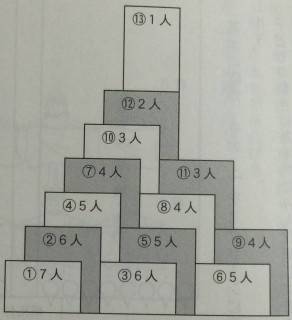
正面から,演技者の顔が見えるのは,①,②,④,⑦,⑩,⑫,⑬の7つの列です.人数は下段から順に,7人,6人,…,1人と,1人ずつ減っています.
番号順にたどると,また別の,興味深い性質が現れます.
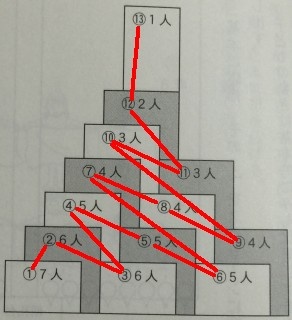
②と③がそれぞれ6人,④と⑤と⑥がそれぞれ5人,⑦と⑧と⑨がそれぞれ4人,⑩と⑪がそれぞれ3人です.
以上より,n段の三角錐型人間ピラミッドを作る手順が少し,見えてきました.すなわち,まず最下段の正面にn人が四つんばいになって並び,次にその上にn-1人が中腰,その後ろにn-1人が四つんばい,…となるわけです.ただ,この考え方では,後ろは何列目まで必要なのかが,明らかではありません.
そこを掘り下げていく前に,関連情報を挙げておきます.三角錐型の7段と10段のピラミッドについては,http://yutaka-nishiyama.sakura.ne.jp/math/artpyramid.pdf*1でも詳しく述べられていますが,上記の本とイラストを参考にしており,それぞれの段の列数の根拠は見当たりません.拙作のhttps://github.com/takehiko/gf/blob/master/text/trigonal.txtでは,3段から11段までのそれぞれについて,段(最下段を1段目としています.後述)・列ごとの人数と配置を手順化しています.
また次のページでは,10段ピラミッドを対象として,さまざまな角度から見ることのできる3Dモデルが載っていま
- http://www.selfi.sh/20160221-021013
段・列ごとの人数について,トップダウンのアプローチで,検討していきます.
ピラミッドのそれぞれの演技者に,識別番号を割り振ることから始めます.「上からi番目,前からj番目,左からk番目の人」を,i.j.kと表します.ピラミッドの段数にかかわらず,トップは1.1.1です.7段の場合,最下段の正面は,7.1.1から7.1.7までの7名,最下段の最後部は,7.3.1から7.3.5までの5名です.kの値に関して,左右の向きは本質的にどちらでもよいのですが,便宜上,「演技者から見て」とします.左端が1です(正面より,ピラミッドを見る者にとっては,右端が1です).
数学的には,n段の三角錐型人間ピラミッドを構成するための識別番号の集合をPnとすると,P7={1.1.1, 2.1.1, 2.1.2, ..., 7.3.5}と表現できます.「...」とごまかすのではなく,要素を特定することが,当面の目標となります.なお,Pnに関連して,Qn={i.j.k|1≦i,j,k≦n,i-j-k+1≧0}と定義すると,Pn⊂Qnとなります.集合Qnは,(離散的な)三角錐の並びに対応しており,たとえばパチンコ玉を並べることで実現できます.またn≧2のとき,1.1.1, 2.1.1, 2.1.2はPnとQnの両方の要素ですが,2.2.1はQnにのみ属し,Pnの要素にはなりません(人間ピラミッドでは2段目は2列にならない,と言うことができます).
次に,上のイラストでも,3Dモデルでも,運動会や演技指導のYouTube動画でもかまいませんが,三角錐型の人間ピラミッドをよく見ると,演技者を次の3つに分けることができます.2人の背中の上に立って手を広げる「トップ」,四つんばいになって手足を地面につける「土台」,それと中腰の姿勢をとる「中間」です.なお,中間のうち下から2段目の人は,地面に足をついていて,それ以外の中間の演技者は,手も足も,より下の段の人の背中の上となります.
段数をnとし,i.j.kの書式で,この3者を区別するなら,トップは唯一,1.1.1です.土台は,i=nです.中間は2≦i<nと表せます.
では,上下関係(荷重をかける・荷重がかかる関係)を,ルール化していきましょう.まずトップの人(1.1.1)は,2段目の2人(2.1.1と2.1.2)の背中に足を置きます.
中間のうち,手も足も誰かの上という人(i.j.k,ただし2≦i<n-1)の依存関係を考えます.識別番号の定義に加えて,ピラミッドの完成形を観察することで分かる関係から,次のルールを得ることができます.すなわち,i.j.kの人は,
- 左手を(i+1).j.kの人の背中に,
- 右手を(i+1).j.(k+1)の人の背中に,
- 左足を(i+2).(j+1).kの人の背中に,
- 右足を(i+2).(j+1).(k+1)の人の背中に,
それぞれ乗せます.そして中間のうち下から2段目の人には,左足と右足のルールを適用しないこととします.
これらから,Pnの要素を特定できます.n=7の場合,すなわちP7については,次のようになります.
- トップの人は…1.1.1∈P7
- 1.1.1を支えるのは…2.1.1, 2.1.2∈P7
- 2.1.1を支えるのは…3.1.1, 3.1.2, 4.2.1, 4.2.2∈P7
- 2.1.2を支えるのは…3.1.2, 3.1.3, 4.2.2, 4.2.3∈P7
- 3.1.1を支えるのは…4.1.1, 4.1.2, 5.2.1, 5.2.2∈P7
- 3.1.2を支えるのは…4.1.2, 4.1.3, 5.2.2, 5.2.3∈P7
- 4.2.1を支えるのは…5.2.1, 5.2.2, 6.3.1, 6.3.2∈P7
- 4.2.2を支えるのは…5.2.2, 5.2.3, 6.3.2, 6.3.3∈P7
- 3.1.3を支えるのは…4.1.3, 4.1.4, 5.2.3, 5.2.4∈P7
- 4.2.3を支えるのは…5.2.3, 5.2.4, 6.3.3, 6.3.4∈P7
- 4.1.1を支えるのは…5.1.1, 5.1.2, 6.2.1, 6.2.2∈P7
- 4.1.2を支えるのは…5.1.2, 5.1.3, 6.2.2, 6.2.3∈P7
- 5.2.1を支えるのは…6.2.1, 6.2.2, 7.3.1, 7.3.2∈P7
- 5.2.2を支えるのは…6.2.2, 6.2.3, 7.3.2, 7.3.3∈P7
- 4.1.3を支えるのは…5.1.3, 5.1.4, 6.2.3, 6.2.4∈P7
- 5.2.3を支えるのは…6.2.3, 6.2.4, 7.3.3, 7.3.4∈P7
- 6.3.1を支えるのは…7.3.1, 7.3.2∈P7
- 6.3.2を支えるのは…7.3.2, 7.3.3∈P7
- 6.3.3を支えるのは…7.3.3, 7.3.4∈P7
- 4.1.4を支えるのは…5.1.4, 5.1.5, 6.2.4, 6.2.5∈P7
- 5.2.4を支えるのは…6.2.4, 6.2.5, 7.3.4, 7.3.5∈P7
- 6.3.4を支えるのは…7.3.4, 7.3.5∈P7
- 5.1.1を支えるのは…6.1.1, 6.1.2, 7.2.1, 7.2.2∈P7
- 5.1.2を支えるのは…6.1.2, 6.1.3, 7.2.2, 7.2.3∈P7
- 6.2.1を支えるのは…7.2.1, 7.2.2∈P7
- 6.2.2を支えるのは…7.2.2, 7.2.3∈P7
- 5.1.3を支えるのは…6.1.3, 6.1.4, 7.2.3, 7.2.4∈P7
- 6.2.3を支えるのは…7.2.3, 7.2.4∈P7
- 5.1.4を支えるのは…6.1.4, 6.1.5, 7.2.4, 7.2.5∈P7
- 6.2.4を支えるのは…7.2.4, 7.2.5∈P7
- 5.1.5を支えるのは…6.1.5, 6.1.6, 7.2.5, 7.2.6∈P7
- 6.2.5を支えるのは…7.2.5, 7.2.6∈P7
- 6.1.1を支えるのは…7.1.1, 7.1.2∈P7
- 6.1.2を支えるのは…7.1.2, 7.1.3∈P7
- 6.1.3を支えるのは…7.1.3, 7.1.4∈P7
- 6.1.4を支えるのは…7.1.4, 7.1.5∈P7
- 6.1.5を支えるのは…7.1.5, 7.1.6∈P7
- 6.1.6を支えるのは…7.1.6, 7.1.7∈P7
上記を手作業でつくるのは,ミスばかりになりますので,Rubyスクリプトを自作し,機械的に求めました.ソースはGistよりご覧ください.コマンドライン引数として,ピラミッドの段数を与えることができます.デフォルトは7段です.それと,Rubyの実行オプションとして-dをつけると,より詳細なメッセージが出力されます.
「3.1.2を支えるのは」の次が「4.2.1を支えるのは」であり,「3.1.3を支えるのは」ではないのは,トップダウンで,必要とするi.j.kを求めているためです.プログラムでは,先入れ先出しのリスト構造であるキューを用いています.具体的には,未処理(その番号の者が必要なのは分かっているけれど,誰が支えるのかは不明)の識別番号のリストを,キューとして持っておきます.初期値はトップの1.1.1のみとします.先頭から取り出して,誰に支えてもらっているかを特定し,新たに得た識別番号が未処理であれば,キューに追加します.順に処理して,キューが空になれば,登場人物がすべて出揃いまして,処理が完了というわけです.
プログラムは,「Xを支えるのは…Y」という形式のあとに,獲得順と,識別番号順の,i.j.kのリストを出力します.7段の識別番号順は以下の通りで,これが,集合P7を過不足なく表現したものとなります.
sorted: ["1.1.1", "2.1.1", "2.1.2", "3.1.1", "3.1.2", "3.1.3", "4.1.1", "4.1.2", "4.1.3", "4.1.4", "4.2.1", "4.2.2", "4.2.3", "5.1.1", "5.1.2", "5.1.3", "5.1.4", "5.1.5", "5.2.1", "5.2.2", "5.2.3", "5.2.4", "6.1.1", "6.1.2", "6.1.3", "6.1.4", "6.1.5", "6.1.6", "6.2.1", "6.2.2", "6.2.3", "6.2.4", "6.2.5", "6.3.1", "6.3.2", "6.3.3", "6.3.4", "7.1.1", "7.1.2", "7.1.3", "7.1.4", "7.1.5", "7.1.6", "7.1.7", "7.2.1", "7.2.2", "7.2.3", "7.2.4", "7.2.5", "7.2.6", "7.3.1", "7.3.2", "7.3.3", "7.3.4", "7.3.5"]
トップダウンに基づく検討により,最下段が何列なのかを,図なしで求めることができます.1〜3段については,1列です.4段と5段は2列,6段と7段は3列と,2段増えるごとに1列増えます.段数nのときは,床関数(小数部分切り捨て)を用いて列と表せます*2.その理由ですが,2.1.1の人を起点に,「左足を(i+2).(j+1).kの人の背中に乗せる(足を置くのは,2段下で1列後ろ)」というルールを繰り返し適用することで,計算ができるからです.
ここまで,何段目かを表すiについて,最上段をi=1としてきました.こうすることのメリットは,ピラミッドの段数を変更することで,浮かび上がってきます.前述のプログラムで,6段,5段に変えたとき,実行結果の抜粋は以下のとおりとなります.
level: 6
persons: 37
sorted: ["1.1.1", "2.1.1", "2.1.2", "3.1.1", "3.1.2", "3.1.3", "4.1.1", "4.1.2", "4.1.3", "4.1.4", "4.2.1", "4.2.2", "4.2.3", "5.1.1", "5.1.2", "5.1.3", "5.1.4", "5.1.5", "5.2.1", "5.2.2", "5.2.3", "5.2.4", "6.1.1", "6.1.2", "6.1.3", "6.1.4", "6.1.5", "6.1.6", "6.2.1", "6.2.2", "6.2.3", "6.2.4", "6.2.5", "6.3.1", "6.3.2", "6.3.3", "6.3.4"]
level: 5
persons: 22
sorted: ["1.1.1", "2.1.1", "2.1.2", "3.1.1", "3.1.2", "3.1.3", "4.1.1", "4.1.2", "4.1.3", "4.1.4", "4.2.1", "4.2.2", "4.2.3", "5.1.1", "5.1.2", "5.1.3", "5.1.4", "5.1.5", "5.2.1", "5.2.2", "5.2.3", "5.2.4"]
5段,6段,7段の(「sorted:」のあとの)リストを比較すると,包含関係をなしているのが分かります.すなわち,5段のピラミッドを構成するのと同じ識別番号は,6段のピラミッドにそのまま登場します.6段のピラミッドを構成するのと同じ識別番号は,7段のピラミッドにそのまま登場します.違いは,新たな(最下)段の情報だけです.
他の隣り合う段数どうしでも,同様です.言ってみれば,n段の三角錐型人間ピラミッドを作ったのなら,その人々を乗せられる土台を用意し,移し替えると,n+1段の三角錐型人間ピラミッドができる,というわけです.なお,n+1段目の人数は,初項n+1,公差-1の等差数列の項までの総和であり,手計算でも容易に求められます.
ここまで,識別番号だけを見比べましたが,上下関係もまったく同じです.なぜなら,上で述べたルールを適用して得られるからです.違いは,下の2段の演技者が地面に体をつけることだけです.
上下関係(荷重をかける・荷重がかかる関係)が同じなので,荷重の不変性も示されます.すなわち,構成する段数が異なっていても,同じ識別番号なら,同じ荷重となります.
これは,多めの段数のピラミッドで荷重を計算しておけば,その値を参照することで,段数を少なくした場合でも荷重が特定できることを意味します.http://www.selfi.sh/20160221-021013(デッドリンク)では,1〜7段目,8〜10段目の負荷がそれぞれ色分けされていますが,使わない段を取り除けば,構築したい段数に合った演技者数と配置,そして(各演技者の自重を1としたときの)かかる荷重が,そこに載っているのです.
ところでgfでは,i.j.kの番号表記について,i=1は最下段とし,上に行くほどこの値が大きくなるようにしています.数日前よりコード改修を行い,本日のコミットで,俵型人間ピラミッド・三角錐型人間ピラミッド・やぐらのすべてにおいて,-cまたは--descendを引数に加えて実行することで,i=1を最上段,下に行くほど大きくなるようなナンバリングで出力するようにしました.
包含関係や,処理の合理性としては,下に行くほど大きくなるナンバリングに軍配が上がりますが,gfでは今後も,上に行くほど大きくなるナンバリングをデフォルトとします.実際に組み上げるのはボトムアップなのに加えて,最下段の演技者を---正面から見えない者も---最も大事にしたいと,考えているからです.
段数についてですが,『体育科教育 2016年 05 月号 [雑誌]』p.64には,ピラミッドの演技図(グラウンド内の大まかな構成図)が載っています.中央には「ピラミッド(7段ピラミッド)」とあります.この学校では7段で組んだのかと思いながら,図の周辺に目をやると,この図のキャプションには「図2 ピラミッドの演技図。生徒たちは当初、周囲に3段、中央に7段を配置していたが、教師の指導を経て5段に修正された。」と書かれていました.
安全な方へシフトした,ということですね.