円と正方形と，五角形

いきなりですが問題です．

円Oと正方形OABCがあり，その半径と1辺の長さは等しい（点Aおよび点Cは，円Oの円周上にある）．さらに，点Dおよび点Eはともに，正方形OABCの内部，そして円Oの円周上にあり，AD＝DE＝ECを満たすものとする．このとき，五角形ABCEDの面積は，正方形OABCの面積の何倍か．

図にします．

五角形の面積の公式，というのを学んだ記憶はありませんので，五角形ABCEDを三角形に分割したいところです．具体的にはBとD，BとEを結んで，三角形BAD，三角形BDE，三角形BECに分け，それぞれの面積を考えるのは，どうでしょうか．この場合，三角形BDEの面積が，容易に計算できそうにありません．
ですが別のところに補助線を引くと，小学校の算数の知識で，面積が求められます．OとD，OとEを結びます．

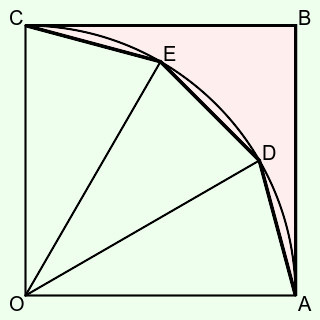
このとき，三角形OADは，OA＝ODの二等辺三角形です．そして，三角形OAD，三角形ODE，三角形OECは，いずれも合同です．そうすると，角AOD，角DOE，角EOCの大きさがいずれも等しく，その和（角AOD＋角DOE＋角EOC＝角AOC）は90度ですので，角AODは30度です．
では，三角形OADの面積は，正方形OABCの面積の，何倍でしょうか．それを知るために，もう一つ，補助線を入れます．AとEを結びます．そしてODとAEの交点をFとします．

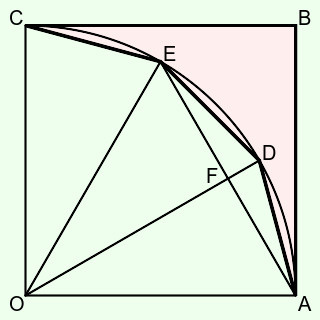
三角形OAEは正三角形です．なぜなら，OA＝OEかつ角AOE＝60度だからです．次に，三角形OAFと三角形OEFは合同であり，AF＝EFですので，AFの長さはAEの長さの半分，そして（AE＝OAなので）正方形の1辺の長さの半分となります．あとは角度ですが，三角形OAFに着目すると，角AOF＝30度，角OAF＝60度ですので，角OFA＝90度です．これは，三角形OADの面積を求めるにあたり，ODを底辺としたときAFがその高さになることを意味します．ということで三角形OADの面積は，OD×FA÷2＝（正方形の1辺の長さ）×（正方形の1辺の長さの半分）÷2となり，整理すると，正方形OABCの面積の4分の1となります．
三角形ODE，三角形OECも同じ面積ですので，五角形ABCEDの面積は，正方形OABCの面積から，「正方形OABCの面積の4分の1」の3つ分を取り除けば求められまして，これもまた，正方形OABCの面積の4分の1となります．

この記事の内容は，少し前から頭の中にありました．2つの辺の長さがaで，その挟む角の大きさが30度のとき，その三角形の面積は，もちろん高校で学ぶ三角比により $\frac12a\cdot a\sin 30^{\circ}$ ＝ $\frac14a^2$ と求められるのですが，三角比なしでも，2つを隣り合わせると正三角形ができることから（したがって小学校の知識で），計算できるのでした．
この図形を，大学教育・情報（プログラミング）教育に~~大学入試の~~アレンジするなら，こうでしょうか．2点D,Eを，正方形OABCの内部，そして円Oの円周上で自由に（ただしA,D,E,Cの順に円周上で並ぶものとして）動かしたときの，五角形ABCEDの面積の上限と下限です．上限*1は，DがAに，EがCに限りなく近づく状態であり，これは三角形ABCの面積を考えればよく，正方形OABCの面積の2分の1です．下限（というか最小値）となるのが，本日の問題のような位置にあるときであれば，数学的に美しいのですが，それを証明するには至っていません．