わさっきhb

大学（教育研究）とか ，親馬鹿とか，和歌山とか，とか，とか．

「日常生活の中で計算が活用できる子供の育成を目指した学習指導の一試み」とその周辺

OoM

発言をたどっていくと，次のようなやりとりがありました．

最後から2番目でリンクされているのは，以下のPDFファイルです．

「計算の意味の理解」として，「【問5】ここに4まいのふくろがあります。かずや君が，1まいのふくろにりんごを3こずつ入れました。りんごは，ぜんぶでなんこありますか。」を出題し，式と絵をかかせています（この問題を，以下では「かずや君のりんごの問題」と書きます）．
かずや君のりんごの問題に対する，インターネット上の評価例は，次のところにあります．その結果から分かることとして，「立式順序で問題状況の理解を測ることはできない」と「絵を描かせれば、問題状況の理解を測ることができる」の2点を挙げています．

その評価なり，今月のツイートなりを見ていると，当該PDFファイルの主眼と，「計算の意味の理解」の出題の位置づけが欠落している点が，気になります．
主眼は，サブタイトルにあるとおり3年の「2位数×2位数」，言い換えると「2けたどうしのかけ算」の指導です．
このことに注意して，文書を通して読むと，5.2節では，レディネスの調査をしていることが分かります*1．かずや君のりんごの問題も，この中にあり，2年で学習した「乗法の意味」がどれくらい定着しているか（忘れず理解しているか）を確認するための出題となっています．解答類型における「正答」「誤答」の出現，また「表４を見ると」から始まる段落の中の「乗法の意味が明確に理解できていない」「問題の文章構成に惑わされることなく，乗法を使った正しい立式ができるように指導していく必要がある」といった表現から，著者はこの出題において正答が何であるかを認識し，それなりの割合で誤答が出現することを想定した上で，出題していると，読むことができます．
当ブログでは，「計算の意味の理解」の調査における一考察をリリースしてきました．本記事はその補訂を試みたものです．


上記PDF文書を，「教育実験」だとか「原著」だとか表現するのには，違和感があります．形式的に見て分かるのは，関連研究がじゅうぶんにあるとは言えないところです．あるいはこれを原著というのなら，学会など適切なところで公表し，CiNiiから検索できたり，算数教育の他の文書から引用されたりするなど，あっていいはずですが，そのいずれも見当たりません．
かけ算を含む演算の意味の理解に対して，児童らの認識を調査している論文として，思い浮かぶものを，挙げておきます．

ところで，かずや君のりんごの問題については，2012年度に類題が出ています．

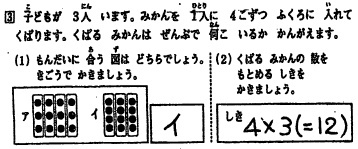
平成24年度実施 学力実態調査の集計と考察〈数と計算 数量関係〉の第2学年，大問3です．「子どもが 3人 います。みかんを 1人に 4こずつ ふくろに 入れて くばります。くばる みかんは ぜんぶで 何こ いるか かんがえます。」と与えたあと，問題に合う図を2つの中から選択させ，その後，式を書かせています．これにより，文章から場面や数量の関係を適切に把握しているか，そして，その関係をかけ算の式で適切に表すことができるかを尋ねています．両方正解したのは54%で，図のみ正解は28%，式のみ正解は6%とのことです．
このうち，「文章から場面や数量の関係を適切に把握しているか」「その関係を式で適切に表すことができるか」については，関連する研究があります．

それぞれから主要部を取り出しておきます．

算数文章題の解法過程は，一般に与えられた文章を読んで理解し，理解した内容に基づいて問題を解くことからなる(Hinsley, Hayes, & Simon, 1977; Mayer, 1982, 1985, 1987; Paige & Simon, 1966)。本研究は，算数文章題の解法過程の前半部である与えられた文章を読んで理解する過程に焦点を当てたものである。
一般に，算数の文章題を読んで理解する過程とは，子どもが与えられた文章題を読んで問題文の内容に適したスキーマを構成することである。(略)
（多鹿ら, 1994, p.125）

算数文章題の解決過程は、理解と解決の過程に分けて考えられる。Lewis & Mayer (1987)では問題文を読んで理解する問題理解過程と、理解したことに基づき解決する解決実行過程からなるとした。またKintsch & Greeno (1985)も理解と解決の2段階にわけ、さらに変換、統合、プランニング、実行の4つの下位過程を想定している。こうした分析について、吉田・多賀(1995)ではスキーマ理論として紹介している。スキーマとは問題として書かれている文章の意味を理解し、内容に関連する知識を利用して文間の関係をまとめあげた知識構造を言う。
スキーマ理論では、文章題を解くプロセスを「理解過程」と「解決過程」の2段階に分けた。(略)
（中山・高山, 20041994, p.163）

「文章から場面や数量の関係を適切に把握しているか」は理解過程に，「その関係を式で適切に表すことができるか」は解決過程に対応します．理解過程・解決過程という2分類は，1980年代までの（海外の）研究において，確立したものと思われます．1994年の上記2文献では，その2つの概念，そしてもっと詳細化された過程を踏まえ，それぞれ目的を設定して量的・質的な調査を実施しています．
理解過程と解決過程，あるいは「文章から場面や数量の関係を適切に把握しているか」と「その関係をかけ算の式で適切に表すことができるか」の区別について，あと一つ，書籍から実践例を紹介します．

田中博史の算数授業のつくり方 (プレミアム講座ライブ)

田中博史の算数授業のつくり方 (プレミアム講座ライブ)

次のノートは，女の子の場合です。(略)でも，これでちゃんと場面の状態を把握しています。
このように描いたのに，もし式を「5×4」と書いたとすると，この子は読み取りができていないのではなくて，式の意味を間違えて覚えているだけとなります。治療するところが変わりますよね。
式を「5×4」と書いた子どもに「ちゃんと文章を読んでごらん」といくら指導してもだめです。この子は逆に覚えているわけですから。絵が図にできたら，その後で算数の言葉に表し直して「4×5」と書くんだよと，ここは確認していいところです。「こういう絵のことを4×5」と言うんだよ」と教えるのです。
(pp.64-65)

はじめのほうで取り上げた，「立式順序で問題状況の理解を測ることはできない」を含む評価例は，理解過程に注目したものであり，その一方で式に表すという解決過程のことをじゅうぶんに考慮しておらず，ミスリーディングをしている，あるいは算数教育の知見をきちんと踏まえていない印象を持っています．
本記事の結論は次のとおり：

  • かずや君のりんごの問題は，乗法の意味に関して理解過程・解決過程を問うものです．間違えたときは，その反応から，2つの過程のどちらに子どもの課題があるかを知ることができます．関連する，その後の出題・実践例もあります．


関連：

関連書：

小学校指導法 算数 (教科指導法シリーズ)

小学校指導法 算数 (教科指導法シリーズ)

教育評価 (岩波テキストブックス)

教育評価 (岩波テキストブックス)

*1:診断的評価とも呼ばれます．