備忘録として作ったTogetterまとめで500 viewを超えたのは久しぶりです.お気に入りやコメントもつき,良いレスポンスは思い浮かばないものの,嬉しく思っています.
さて,このまとめを作るきっかけとなった記事,http://www.jiftm.org/yujakudo/miscellany/order-of-mult/(リンク切れ)について,1点,気になっていた記述がありました.
かけ算の順番による混乱
Wikipediaには以下の様な記載があります。
また、一旦、絵にもとづいて式と答えを書くことができるようになった児童が、かけ算の順序を指導された後、文章題が解けないと言い出し、式を書くのを躊躇するようになった例が報告されている。
(宮田佳緒里・海老名正司・工藤与志文 ,「かけ算の意味理解を促すための問題状況の図示の試み」,教育ネットワークセンター年報: 53-60,2011)これは可愛そうですね。
この文献は,wikipedia:かけ算の順序問題の参考文献でリンクされていて,PDFファイルが無料で読めます.「宮田ら(2011)」は後方参照用のラベルです.
通して読めば分かるように,教える側が教材を準備・提示し,対話を通じて,児童が正しい順序で立式できるようになったという内容です*1.「式を書くのを躊躇するようになった例」として無批判に引用し,「かけ算の順番による混乱」「これは可愛そうですね」と書いてあるのには,ネットリテラシーは大丈夫なのかと思わざるを得ません.
宮田ら(2011)では,実施した指導法の効果や意義を述べる中で,対象児Yはどのように知識構造を変化していったのかを,先行文献を挙げながら考察しています.
それでは,本校の学習支援プランには,文章題解決におけるどのような困難を克服する効果があったのだろうか。Mayer (1992)は,算数文章題を解決する際の心的過程を4段階―解釈段階,統合段階,プランニングとモニタリング段階,実行段階―に分けた。このうち,Yが困難とした,式の順序とかけ算の意味との対応づけは,統合過程におけるつまずきである。統合過程では,問題タイプについての知識(スキーマ的知識)に基づいて,文章題から読み取った情報のうちの適切なものが選択・統合されて,文章題全体についての心的表象が構成される。Mayer (1992)によれば,スキーマ的知識には,例えば「面積の問題は,面積=縦×横という公式に基づく」のように,式についての知識が含まれる。「一あたり量がいくつ分」というかけ算の文章題で言えば,スキーマ的知識は「一あたり量がいくつ分というかけ算の問題は,全体量=一あたり量×いくつ分という式に基づく」のように表現できる。一方,Yは式の順序とかけ算の意味との対応づけが不十分であったことから,Yが有していたスキーマ的知識は「かけ算の問題は,全体量=ある数×他の数という式に基づく」のような不十分な状態であったと考えられる。そこで,問題の状況を表す絵を取り入れた教材に即して学習することにより,式の順序とかけ算の意味とが正しく対応づけられ,スキーマ的知識がより精緻なものになったと考えられる。以上のことから,問題の状況を表す絵に即して,式の順序とかけ算の意味とを対応づける学習支援プランは,算数文章題解決の統合過程における困難を克服する効果があったと考えられる。
(p.59.強調は原文では下線)
Mayerの名前には,見覚えがあります.「日常生活の中で計算が活用できる子供の育成を目指した学習指導の一試み」とその周辺で書きました.ただし文献は異なります.そこでは「... Mayer, 1982, 1985, 1987 ...」「Lewis & Mayer (1987)」として,1980年代のものが引用されています.
Mayerの文献は読んでいませんので,推測ですが,今のところ次のように理解しています.まず1980年代には,児童らが文章題を解くプロセスを,「理解過程」と「実行過程」という2段階でモデル化するのが,確立していました.その後,それぞれ2つずつに詳細化し,例えば「解釈段階」「統合段階」「プランニングとモニタリング段階」「実行段階」という名称のもと,4段階によるモデルが提唱されたというわけです.
これまで見てきた出題例と照らし合わせておきます.
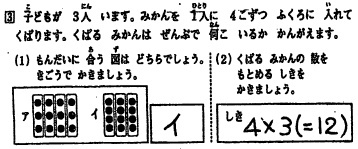 (出典)
(出典)
このうち(1)は,2段階モデルだと「理解過程」,(2)は「実行過程」を問う,と見ることができます.4段階モデルに基づくなら,(1)は「解釈段階」で,(2)は「統合段階」「プランニングとモニタリング段階」「実行段階」*2になります.
この詳細化は,本日未明に言及のあったツイートへの示唆を与えるものとなっています.
「分かっている」のが,理解過程あるいは解釈段階という最初のところのみである,という可能性です.それ以降の過程・段階まで,[twitter:@tsatie]さんのお子さんが「分かっている」かどうかは,明らかではありません.この件は,@tsatieさんのみならず,図の理解状況を根拠として「ちゃんと理解しているではないか」と批判している,以下の件にも当てはまります.
- 事例:日常生活の中で計算が活用できる子供の育成を目指した学習指導の一試み−「算数日記」を活用した3年「2位数×2位数」の授業実践を通して−
- 代表的な批判:「掛け算順序固定」問題対策本部 - atwiki(アットウィキ)
- 当ブログで書いてきた見解:「計算の意味の理解」の調査における一考察,「日常生活の中で計算が活用できる子供の育成を目指した学習指導の一試み」とその周辺
何をもって「分かっている」と判断すれば良いかは,学習事項に依存します.宮田ら(2011)では上記のとおり,統合段階に「一あたり量がいくつ分というかけ算の問題は,全体量=一あたり量×いくつ分という式に基づく」を入れています.「一つ分の数×いくつ分=全体の数」を根拠とする文献は,いくらでもあります(一番のお勧めは,『小学校指導法 算数』).なお,宮田ら(2011)のFigure1およびFigure2(いずれもp.57)では,図に対応する式を問う際,「7×2=14 と 2×7=14 の どちらでも いい。」「4×8=32 と 8×4=32 の どちらでも いい。」を選択肢に入れていますが,それを正解とする意図は読み取れませんし,やりとりにも見られません.
研究なんてどうでもいいのだ,我が子が「正しく」理解していることが大事なのだ,それを認めてくれないのがダメなんだ,ともしおっしゃるのなら,「何について」正しく理解しているかを問うているのが,昨今の算数教育事情なのだ,と個人的には思っています.都算研調査のかけ算文章題の変更(6年は鉄のぼう,2年はみかん)も,その一つです.
宮田ら(2011)には続報があるので,リンクしておきます.
第一著者と第二著者,そして対象児が同一となっています.年度が進んでおり,わり算の指導について報告をしています.3. 等分除と包含除(アリとキリギリス)でも取り上げました.
「ところで,今回,Yが式の表す意味を図示できるようになったことは大きな進歩と言える」(宮田ら, 2012, p.44)は,子どもの成長を長期にわたって見届けることのできる支援者にとって,励みになったことと思います.分野も年齢も違いますが,私も,学生の成長を喜び,つまずきにはその状況に応じたサポートをしなければと思いながら,教育研究の日々を送るとします.
*1:http://d.hatena.ne.jp/takehikom/20121105/1352042888にも書きましたが,乗法の意味の理解について書かれた諸文献の中では,「正しい順序」という言葉の使用が異例だなという感触を持っています.
*2:その調査では,(1)が正解で(2)に「3×4(=12)」と書いた児童について,4段階モデルのどの段階で誤りが発生したかの特定はできません.2つの数をかければいい(積が求められる)と理解し,「3×4」と書いた子もいれば,頭の中で4×3になる状況だと認識していながら答案には「3×4」と書いた子もいたと思います.その意味で,この出題は2段階モデルのもとで解釈するのがより適切と言えます.もっと細かく,どの段階で誤ったのかを分析するには,数万人規模の調査よりも,1名あるいは小人数を対象とした観察のほうが適しているでしょう.