大きめの書店に足を運び,何冊か購入しました.その中から2冊を取り上げます.
1. 3×2の本を作ろう
書名にある「6つの視点」は,「比べる」「当てる」「作る」「数える」「仲間を見つける」「表す」からなります.かけ算の指導例が,「作る」の中にありました.板書は以下のとおり(p.81).
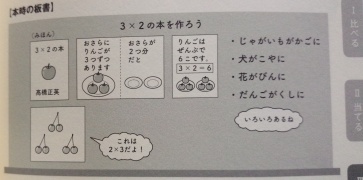
いつものように文字にしておきます.「3×2の本を作ろう」という授業です.1枚の紙を横長にし,横方向に折り曲げれば,4ページからなる本を作ることができます.「みほん」の最初のページは,タイトル「3×2の本」と作者,そして中央にりんごの絵があります.ここから,りんごがいくつあるかを求めるのだなと想像できます.
開くと,その左には,「おさらに//りんごが//3つずつ//あります」という文字と,1枚の皿にりんごが3つ乗った絵があります.右には,「おさらが//2つ分//だと」と書き,りんごの乗っていない皿が2枚です.
開いた左側を動かさず,右側を左に倒して,左側と重ねたら,最後のページが出てきます.上から下に向けて,「りんごは//ぜんぶで//6こです。」の文,箱囲みされた「3×2=6」の式,そしてそのかけ算の式に対応した,皿とりんごの絵が,配列されています.
ここで他の書籍と照合します.というのも,かけ算の本づくりは,『板書で見る全単元・全時間の授業のすべて 小学校算数2年〈下〉』(p.70)にもあります.そこでは,見開きを使って1つの場面を表しています.最後のページは,かけ算の式と答えのほか,半具体物であるブロック(タイル)の絵で構成されています.
そこから違いも見えてきます.りんごの3×2の本だと,見開きの左には,かけられる数に関する情報が,右には,かける数に関する情報が書かれています.これにより,かけられる数とかける数の区別がより明確となっています.さらに,この4ページで起承転結の構成になっている---りんごのない,2枚の皿が「転」!---というのも,面白いところです.
これらを考慮すると,先例を踏まえ,かけ算の式の読み,そしてかけ算における2数の理解に関して,さらに効果を高めたものとなっています.
板書に戻りましょう.左下には,さくらんぼの絵に「これは//2×3だよ!」の吹き出しが添えられています.実際,2つずつのさくらんぼが3つ分と見て,2×3なのが分かります.
ここからは,撮影画像の下に書かれている内容です.そこでは4人の子どもの発言が,吹き出しになっています.最初の子どもは「「ずつ」と「分」が大切な言葉だよね」,最後の子どもは「3×2と2×3の答えは同じだけど,意味が違う!」と言っています.ともに,2年でかけ算の意味を学習し,式から場面を作ろうとする際には,大事な要素だと思います*1.
この本をざっと見て,2年のかけ算と別に,面白かったのが3点ありました.わり算の授業で,「72こ」を起点に,2でわるのを3回,3でわるのを2回,したときの図が,学生時代に学んだ,項書換え系の合流性の図と同じ形なのでした.ここで「2でわる」のと「3でわる」のは順不同です.実際,72こを起点として,2でわってからまた2でわりそして3でわっても,2でわってからこんどは3でわりそして2でわっても,3でわってから2でわりそしてまた2でわっても,途中の個数は異なりますが結果としては「6こ」となります.「2でわる」操作が左下方向,「3でわる」操作が右下方向となっている図なのです.
2番目は,引っかかりどころです.出版社は東洋館だし,参考文献に載っているのは1冊を除いて筑波関係者の本なのですが,本文中に「1あたり」の表記が目につきました.2件あって,まずは2年の「かさ」の解説(p.35)の「量と測定領域の基本は「1あたりの考え方」である」,もう一つは5年の「単位量あたりの大きさ」(p.156)で,タイトルのすぐ下そして本文中に見られる「1あたり」(カギカッコ囲み)です.「1あたり」の用語を採用した意図は,ちょっと推測できません.
最後は「かけ算の順序」がらみです.6年の「文字を使った式」の中で,y=8×xという式を提示し,これは何を表したものだろうと問うています(pp.158-159).板書では,「xの8倍」「比例」が箇条書きに,「もしyが面積で//底辺がxだったら//8が高さ」「もしyが//周りの長さ//だったら//xは正八角形の//一辺の長さ」が吹き出しになっています.この学年になれば,8×xを「8のx倍」だけでなく「xの8倍」と読んでもよいことを示唆しています.
2. 江戸しぐさの正体 第三刷
「二〇一四年一〇月二日 第三刷」の本を入手しました.かけ算の件が修正されていました(p.197).文字単位で差分をとると:
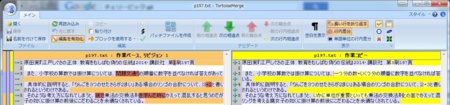
(画像をクリックしていけば,オリジナルサイズの比較的きれいなスクリーンショットが得られます.)
修正を見届けることができ,少し安心できました.ともあれ,自分のテリトリー外の話題について,1件の情報源をもとに,独自に要約しようとすると,刊行されるまで誰も「これ,おかしいんじゃないの?」と指摘する人が出ない,というのは,私自身も何か書く際には,注意をしていこうと思います.
この本では,かけ算の話は『かけ算には順序があるのか (岩波科学ライブラリー)』のみを参考資料に入れているので,「2011年11月15日 第4刷発行」の本も,書店で同時に購入し,読み直しました.
「1つ分の数×いくつ分」という表記を,本文p.1ほかで見つけることができました.
なのですが,『江戸しぐさの正体』第3刷で挿入された「いかに単位が重要といっても」について,これに対応しそうな記述を,見つけることができませんでした*2.
『かけ算には順序があるのか』のまえがきや第1章のはじめに取り上げている問題は,「6人に4個ずつミカンを配ると,ミカンは何個必要ですか」という,基準量が後に示されたタイプです.それに対し『江戸しぐさの正体』では,第1刷も第3刷も,「「りんごを3つのせたさらが2まい」ある場合のリンゴの合計」ですので,基準量(一つ分の数)が先です.そのタイプで,導入時において,逆に書いてしまう子どもに注意せよという本は,また別のものを見ないといけません(例えば『算数子どもの考え方教師の導き方 2年』).
あとは「かけ算」を,算数教育・初等教育の観点で見るか,文献・事例を組み合わせて実態(経緯や現状)を浮かび上がらせようと試みるのか,自分の気に入ったものだけをつまみ食いしようとしたいのかが,人それぞれで違ってくるのかなとも思います.
「自分の気に入ったものだけをつまみ食い」は,英語だとcherry-pickingという1語で表せます.情報通信関連では,Gitでcherry-pick(チェリーピック)が活用されています.
本日取り上げた2冊の本では,「りんごを3つのせたさらが2まい」に対し,一方は3×2の式で表せることを奨励し,もう一方は2×3は不正解とすることを批判しており,対照的でした.さくらんぼは『「6つの視点」でつくる算数の授業』で,2×3を表すのに使用しているのが,いい味を出しています.
*1:「かけ算は常に「ずつ」と「分」がいるのか?」というと,もちろんそんなことはなく,算数教育の本から容易に検証できます.かけ算の式で表せる場面を増やしていきながら,既習内容と関連づければいいのです.当ブログで書いてきた中からだと,http://d.hatena.ne.jp/takehikom/20131226/1387983600やhttp://d.hatena.ne.jp/takehikom/20140131/1391118525で見ることができます.今回見てきた本作りの段階で,学習しているかけ算は,「同数のグループ」のタイプです.「同数のグループ」の位置づけについては,http://d.hatena.ne.jp/takehikom/20111013/1318452890をご覧ください.
*2:「単位」が曖昧なようにも感じます.「りんごを3つのせたさらが2まい」という場面において,単位とは何でしょうか? 「一つ分の数」のことだとするなら,(りんご)3つが該当します.それと別に,「つ」「まい」といった助数詞を,単位と同等視することも可能です.

