ファンタジーの法則，1982年だと

筆者が個人的に、ファンタジーの法則と呼んでいる問題解決法についてお話しましょう。ファンタジーというのは別世界と行き来する物語のことで、ファンタジーの法則とは、別世界と行き来することで問題をうまく解くという法則です。
【ファンタジーの法則】
「こちらの世界」で解けない問題があったら…
(1) 問題を「こちらの世界」から「別世界」に持っていきます。
(2) そして、問題を「別世界」で解きます。
(3) 最後に、得られた答えを「こちらの世界」に持って帰ります。

（『プログラマの数学』pp.238-239）*1

算数教育の洋書を読んでいると，非常に似通った図を見かけました．

書誌情報（少し端折っています）は次のとおり．

Riley, M. S., Greeno, J. G., and Heller, J. I.: Development of Children's Problem-Solving Ability in Arithmetic, isbn:0122847806, pp.153-196 (1982).

なのですが，章全体をPDFで読めます．図については，以下のURLでアクセスできます．

http://files.eric.ed.gov/fulltext/ED252410.pdf#page=17

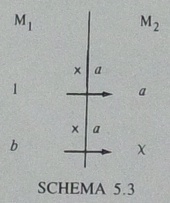
似てはいるものの，よく見ると，違いもあります．Rileyらの図では，流れは逆Uの字型で，出発点となる"Problem Text"は左下です．それに対し結城本の図では，流れはコの字型で，出発点の「問題」は左上です．
そして，2×2のグルーピングが異なります．『プログラマの数学』の図では，「こちらの世界」と「別世界」による分割によって，4つの情報のうち1番目（問題）と4番目（解答）で1つのグループ，2番目（問題）と3番目（解答）*2でまた1つのグループとなっていますが，Rileyらでは1番目の"Probelm Text"と2番目の"Schematized Problem Representation"の上に，[Problem Schemata]が，また3番目の"Schematized Action Representation"と4番目の"Solution"の上に，[Action Schemata]が，それぞれ書かれています．
共通点もあります．問題＝"Problem Text"から，ただちに解答＝"Solution"を得るのが困難なときに，別＝"Schematized"の表現形態に移し，そこでよく知られた方法*3でもって式にし，答えを求めよう，という流れを，見ることができます．
グルーピングが異なると書いたものの，Rileyらの図の2番目と3番目において，"Schematized"と"Representation"でサンドイッチしているのは，結城本の図の「別世界」と同等のことをしていると解釈できます．
この事例でもって，ファンタジーの法則には元ネタがあるだとか，ましてや結城浩氏がパクったと主張したいわけでもありません．経験的に得たことを，形にすると，類似したものになる，という事例がまた一つ増えたといったところでしょうか．

ついでに，図の配置に関する国内外の違いと言えば：