いきなりですが問題です.以下の作りかけの図に,語句などを書き入れて,図を完成させてください.
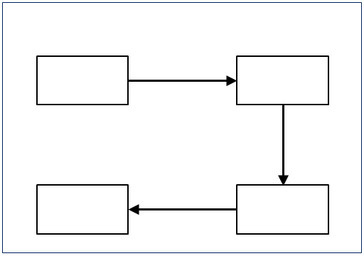
講義の授業前テストです.この日の授業のテーマは「セキュリティ基礎」で,「問題を解くとはどういうことか」という問題意識から始まり,個別問題と問題との違い,問題を解く計算機の抽象化としてのチューリング機械,決定性と非決定性の違い,オーダー,多項式時間と指数時間について,いくつかは以前の復習,いくつかは新規の事項として解説し,P≠NP予想へと持って行きました.
といったところで元ネタです(授業では,解答例①として提示しました).

オリジナルは,『プログラマの数学』のp.239です.Kindle版を参照しています.

- 作者: 結城浩
- 出版社/メーカー: ソフトバンククリエイティブ
- 発売日: 2005/03/24
- メディア: 大型本
- 購入: 41人 クリック: 707回
- この商品を含むブログ (387件) を見る
ことわざだと,「急がば回れ」がぴったりです.そして日常生活にも使えます.自宅から車で,下道(一般道)をえっちらおっちら走って,目的地に着くのは,それが最短経路であったとしても,最短時間であるとは限りません.時間が最優先であれば(そして都合良く,道がついていれば),高速道路を使うことで,早くたどりつけます.図にしました(解答例②です).
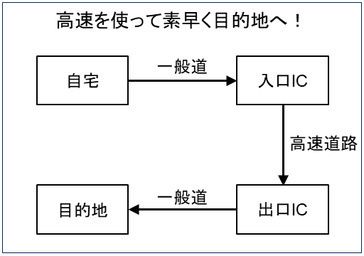
なのですがこの件,『プログラマの数学』のp.239で文章になっていました.
自室に戻って答案を見ていくと,以前の授業前テスト*1の影響か,「起」「承」「転」「結」を入れたものが何件かありました.微分・積分方程式のかわりに「回路方程式」を挙げたのが複数いました.以下のような,大喜利で座布団をもらえるかもらえないか不明な答案も,見かけました.
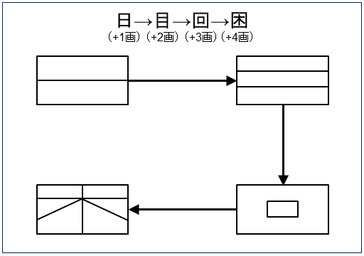
解答例①の図から学ぶべきなのは,与えられた問題を,すでによく知られた他の問題に「帰着(還元,変換)」して解くということです.当ブログで3件とサブブログで1件,『プログラマの数学』の記載にちなんで「ファンタジーの法則」の名前を使い,記事にしていました.