円3分割 - わさっきhb

いきなりですが問題です．

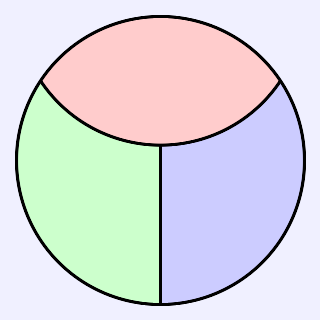
円に対して，次のように2本の線分によって3つに分割し，それらの面積が等しくなるようにしたい．どのようにして分割すればよいか，答えなさい．

どこかから取ってきたというのではなく，オリジナルの出題です．と言いたいのですが，京都を散歩していたときに目にした図形でした．
正三角形については以前に作図しています．

なお，次のように線を引くのではない点にも注意しましょう．

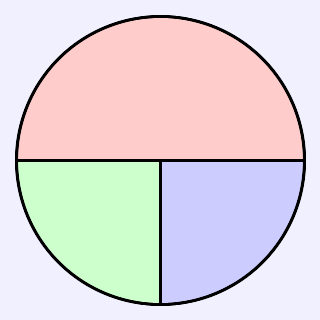
これでは，面積比が2:1:1になります．冒頭の問題は，面積比を1:1:1にせよというものです．正三角形と異なり，定規とコンパスで作図するのは困難と思われます．
解答の前に問題です．

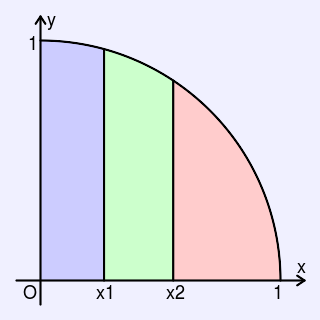
四分円に対して，次のように2本の線分によって3つに分割し，それらの面積が等しくなるようにしたい．どのようにして分割すればよいか，答えなさい．

こちらを先に解き，その結果を使って，円の3分割を行います．
四分円（ $x^2+y^2\leq1$ ，x≧0，y≧0）の3分割について，引く2本の線分はY軸に平行とし，それぞれのx座標をx1，x2（x1＜x2）とします．四分円の面積はπ/4ですので，次の式を満たすx1およびx2を求めます．
$\int_0^{x1}\sqrt{1-x^2}dx=\pi/12$
$\int_0^{x2}\sqrt{1-x^2}dx=\pi/6$
左辺の積分について，http://www004.upp.so-net.ne.jp/s_honma/circle/circle4.htmの情報を参照しながら，x＝sinθとして置換積分を行います．求めたいx1，x2に対応する値をθ1，θ2とすると，式は次のようになります．*1
$\frac12\theta_1+\frac14\sin2\theta_1-\pi/12=0$
$\frac12\theta_2+\frac14\sin2\theta_2-\pi/6=0$
これを解けばいいのですが，解析的に求められそうにないので，ニュートン法を用いました．Rubyに，bigdecimal/newtonライブラリ*2が入っています．
1変数の問題として，コードを書いて解いたところ，次のようになりました．
θ1＝0.267983（＝15.3543度），x1＝0.264787
θ2＝0.586311（＝33.5932度），x2＝0.553292
円の3分割を行う前に，もう少しだけ検討をします．上の積分の式を，少しだけ変えると，次のようになります．
$\int_{x1}^1\sqrt{1-x^2}dx=\pi/6$
四分円を，直線x＝x1で切ったときの右側の面積は，π/6です．なので半円（ $x^2+y^2\leq1$ ，x≧0）を，直線x＝x1で切ったときの右側の面積は，π/3です．これで，円の3分の1が得られました．残りはX軸（y=0）で切れば，上半分も下半分も同じ面積，すなわちπ/3です．
円の式 $x^2+y^2=1$ に対し，A(x1,y1)，B(x1,-y1)，C(-1,0），D(x1,1)，と座標を定めます．ただし $y1=\sqrt{1-x1^2}$ です．そうすると，線分AB，線分CDをそれぞれ結べば，3つの領域ができ，みな等しい面積となります．言ってみればこうです．

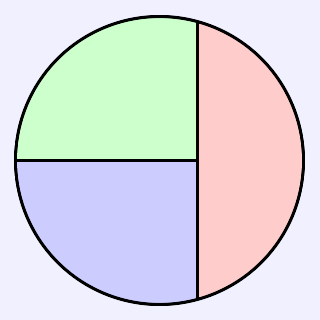
最後に，回転させれば，冒頭の画像の出来上がりです．
さらにですが問題です．

円に対して，次のように円弧と線分によって3つに分割し，それらの面積が等しくなるようにしたい．どのようにして分割すればよいか，答えなさい．

京都で見かけたのはたしか，こっちの図形だったはずです．それはさておき，四分円の3分割で求めたx2を活用すると，図を作ることができます．E(x2,y2)，F(x2,-y2)，ただし $y2=\sqrt{1-x2^2}$ とします．線分EFでは，弓形図形（下図の色付き部分）の面積は，円の6分の1となります*3．

この分割線が対称の軸となるよう，下図のように円を描けば，2つの円弧で囲まれる図形の面積は，円の3分の1です．

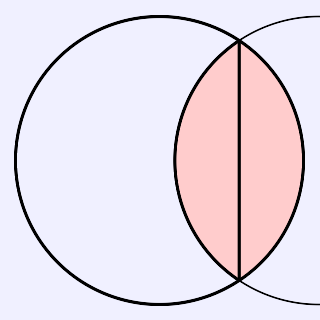
残りを2分割するのにも，少しだけ，座標の計算をします．G(-1,0)はいいとして，H(x3,0)としたとき，x3＝1−2（1−x2）となります．線分GHにより，残りを2等分することができました．あとは，分割を表すのに使わない線分と円弧を取り除き，90度回転させれば，出来上がりです．

描画はRubyとRMagickライブラリを用いました．ニュートン法による求解と合わせて，自作したコードをgistに置いておきます．
コーディングにあたっては，有効桁数を小さめにしました*4．何も考えないでコーディングすると，画像サイズを大きくしてみたときに，「…in `draw': Memory allocation failed `No such file or directory' @ fatal/draw.c/DrawImage/3113 (Magick::FatalImageMagickError)」というエラーが出ました．公開したコードでは，3200x3200の画像も作成できます．
それと，「さらにですが」の3分割の色塗りにおいて，どの分割図形も，2つの円弧の描画を必要とします．円弧のパラメータ指定*5にはいつも悩まされるのですが，コードにしてみると，立てるべきフラグは必要最小限で済みました．

以下自分用メモ：

$ sudo apt-get install python-numpy python-scipy python-matplotlib ipython ipython-notebook python-pandas python-sympy python-nose
$ python
Python 2.7.6 (default, Mar 22 2014, 22:59:56)
>>> from sympy import *
>>> x = Symbol('x')
>>> a = pi / 4
>>> a.evalf()
0.785398163397448
>>> (integrate(sqrt(1 - x * x), (x, 0, 0.264787)) / a).evalf()
0.333155203051047
>>> (integrate(sqrt(1 - x * x), (x, 0, 0.553292)) / a).evalf()
0.666665911206241
>>>

（最終更新：2015-04-02 早朝）

*1:TeX表記ではθ1，θ2はそれぞれ $\theta_1$ ， $\theta_2$ で表しています．