長方形でもひし形でもない平行四辺形は，線対称でない

全国算数授業研究会公式HP
- 月報
  - 算数授業通信293号 (令和5年3月31日)
    - 実践報告①「平行四辺形は線対称？」(page1966)

　報告者は関根哲宏氏です．6年生の授業です．正方形・長方形・平行四辺形・ひし形・台形のそれぞれについて，点対称か，線対称か，そして線対称の場合には対称の軸の数が，表になっています．なお「対称の軸」は，「点対称」「線対称」「対称の中心」と並んで，現行の小学校学習指導要領のもとでは算数の第6学年の〔用語・記号〕に含まれています*1．
　表を見て，えっと思いました．というのも，線対称な台形が存在するのです．具体的には等脚台形です．

　ということで，表の○は，正方形をはじめ各行の図形について常に成り立つ（点対称または線対称である）ことを意味し，×は，その図形では成り立たない場合があると読むのが良さそうです．
　自分なりに，作図してみました．長方形の対称の軸は，「向かい合った2つの辺それぞれの中点を結んだ直線」です．2本，あります．

　次に，ひし形の対称の軸は，「対角線」です．こちらも2本，あります．

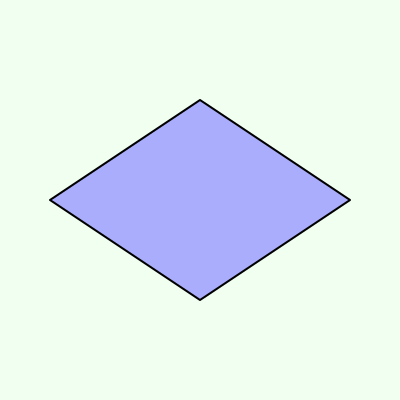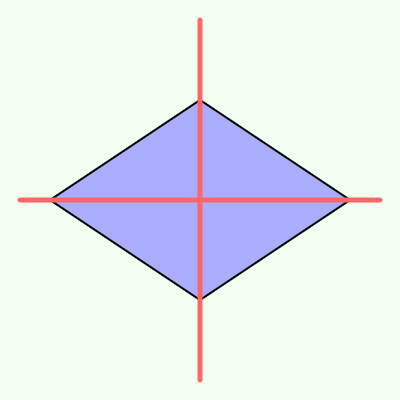
　正方形は，「長方形の対称の軸とひし形の対称の軸の両方」です．合わせて4本です．

　再掲となりますが，等脚台形の対称の軸は，「平行な2つの辺それぞれの中点を結んだ直線」です．これは1本だけです．

　あともう一つ，凧形も線対称です．対称の軸は，「隣り合って長さが等しい2つの辺の交点（頂点）それぞれを結んだ直線」となります．こちらも1本だけです．

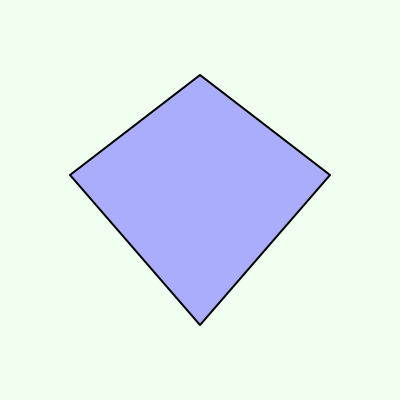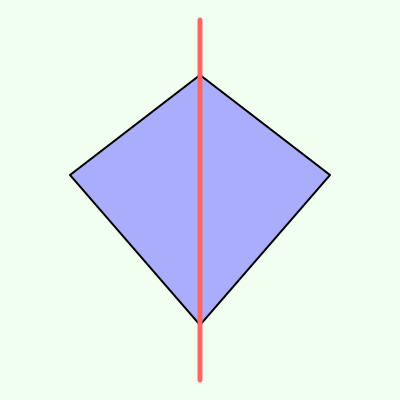
　「×は，その図形では成り立たない場合がある」と書きましたが，それでは平行四辺形について，線対称なものはあるのでしょうか．

　「長方形でもひし形でもない平行四辺形は，線対称でない」が証明できそうです．
　対称の軸の性質として，「平面図形が線対称であるとき，対応する点を結ぶ線分は，全て折り目にした直線によって垂直に二等分される．この直線を対称の軸という．」を挙げることができます．これは，『小学校学習指導要領（平成29年告示）解説算数編』p.293を改変したものです．
　1個の線対称な多角形に限定---曲線を含む図形や，複数の閉領域を1個の図形と見なすことを，除外しています---して，検討することで，その多角形のある辺（辺の両端となる頂点を除く）が，対称の軸と交点を持つとき，「その辺と対称の軸は直交する」と言えます．対称の軸が，多角形の頂点を通ることもあります．頂点を通るときには，対称の軸はその頂点の角の二等分線となり，辺と交わるときには，交点の近くの線分（辺の一部）が180°の角を構成していると見なして，その二等分線となっています．
　それでは証明です．背理法を使用します．「線分XY」と「直線XY」を区別し，「XY」とは書かないようにしているため，字数は多くなります．
　長方形でもひし形でもない平行四辺形ABCDについて，線対称であると仮定します．
　そして一般性を失うことなく，対称の軸ℓは線分ABと交わるものとします．ここには2つの注釈が必要です．まず，多角形が線対称であるとき，対称の軸が多角形のどの辺とも交わらずまたどの頂点も通らない，とすることはできません．次に，ℓは平行四辺形のどの頂点も通りません．もしいずれかを通るとき，線分AB，線分BC，線分CD，線分DAの長さはみな等しく，四角形ABCDはひし形になります．
　ℓにより，点Aと，残りの3点B，C，Dのいずれが対応するかで，場合分けします．
　(i) ℓにより，点Aと点Bが対応する：ですが∠A≠∠Bのため，そのようなℓは対称の軸にはなりません*2．
　(ii) ℓにより，点Aと点Cが対応する：このときℓは，線分ACの垂直二等分線となります．そして，ℓと線分ABは直交しません（「ℓ⊥直線AB」「ℓ⊥直線AC」「A，B，Cは同一直線上にない」を満たす直線ℓおよび3点A，B，Cの組み合わせは存在しません）．ℓと線分ABの交点をEとすると，場合分けより前に書いた通り，点Eは点A，点Bのいずれでもなく，線分ABの内部の点となります．「多角形の辺（辺の両端となる頂点を除く）が，対称の軸と交点を持つ」にもかかわわらず，「その辺と対称の軸は直交する」を満たしません．したがって，ℓは対称の軸ではありません．
　(iii) ℓにより，点Aと点Dが対応する：ですが∠A≠∠Dのため，そのようなℓは対称の軸にはなりません．
　以上より，いずれの場合も，ℓが平行四辺形ABCDの対称の軸であることと矛盾します．（証明終）
　四角形の包含関係として，台形⊂平行四辺形，平行四辺形⊂長方形⊂正方形，平行四辺形⊂ひし形⊂正方形はよく知られていますが，対称の軸の存在（構成の関連性）に関しては，凧形＜ひし形＜正方形，等脚台形＜長方形＜正方形という2種類に分けられます．
　凧形が，四角形の包含関係に陽に現れない一方で，対称の軸に着目した関係だと平行四辺形が出現しない，と言うこともできそうです．