画像作成その1
やり直しですが問題です.
(a)の画像から(b)の画像を作りなさい.
この問題は右ローテートとトランスポーズの作り直しで,画像は,番号をつけなくても巡回の順番が分かるよう変えたという次第です.「右ローテート」は,おかあさんといっしょのコーナーの一つ,「ポコポッテイト」をもじったのでした.
(a)の画像は,次のコマンドで作りました.
$ convert -size 200x120 xc:white -stroke blue -strokewidth 2 -fill none -draw "polyline 20,20 20,100 60,20 60,100 100,20 100,100 140,20 140,100 180,20 180,100" -strokewidth 1 -draw "stroke-dasharray 2 4 path 'M 40,2 v 200' path 'M 80,2 v 120' path 'M 120,2 v 120' path 'M 160,2 v 120' path 'M 0,40 h 200' path 'M 0,80 h 200'" 3a.png
新規に作成するときのイディオムは,「convert -size 幅x高さ xc:色」なのですね.線や丸などの描画については,以下の情報を活用しました.
- http://www.imagemagick.org/script/command-line-options.php
- http://www.imagemagick.org/Usage/draw/
- http://www.w3.org/TR/SVG/paths.html
で,変換方法ですが,右に90度ローテートする,
だと,問題文に載せた画像,すなわち

が得られます.
ちなみにtransposeについては
Mirror the image along the top-left to bottom-right diagonal.
This option mathematically transposes the pixel array. It is equivalent to the sequence -flip -rotate 90.
-transpose
とあります.訳すと
左上から右下への斜め方向を軸として,画像を反転する.
このオプションは画素を数学的な意味で転置する.-flip(上下反転)してから-rotate 90(右方向に90度回転)と等価である.
上下反転してから90度右回転で転置…なるほどです.念のため,「convert 3a.png -flip 3a_flip.png」でできる画像を貼り付けておきます.

画像作成その2
もう一つおまけに問題です.
これには元ネタがあります.汝の隣人のブログを愛せよ | LOVELOGです.
さっそく,式を書くと,2×3×4=24で答えは24個です.これは総合式というやつで,分解式にする場合,2つの考え方があります.
一つ目の考え方は,2×3=6としてから,6×4=24とするものです.ここで「2」は

を意味し,「2×3=6」は
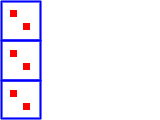
という図に対応づけられます.
サンドイッチの方式で単位を付けて書くと,2個×3=6個,6個×4=24個となります.数教協スタイル*1で単位を付けて書くと,まず2個/箱×3箱=6個として,これを1当たり量とするために6個÷1列=6個/列とし,それから6個/列×4列=24個となります.
「2×3×4=24」と書いた総合式について,サンドイッチ&倍概念では,「(2個×3)×4=24個」です*2.数教協スタイルで表すと,「(2個/箱×3箱)÷1列×4列=24個」となるべきところ,少し変形して「2個/箱×3箱/列×4列=24個」とすることができそうです.
もう一つの計算方法は,3×4=12としてから,2×12=24とするものです.このとき「3×4=12」は,お菓子を無視して小箱の数を計算していることになります.図は次のとおりです.

単位を付けた式を,考えてみます.まず小箱の総数について,サンドイッチの式では「3箱×4=12箱」と表せます.ところで最初に式を「2×3×4」と書きましたが,これを「2×4×3」にしたりだとか,「3×4×2」にしたりしてもいいのかといったことについては,本日のエントリでは対象外とします.かつて調査した中では,山梨のケース,新潟のケースの山梨のほうが,最も関連していると思います.
12箱のそれぞれに,お菓子を2個ずつ入れるとなると,式は2×12=24です.この計算は現在(2年前から),小学2年生でも学ぶそうですが,それはさておき,ここに単位を付けると,「2個×12=24個」です.「12箱」から単位を取り除いて「12」としていますが,サンドイッチ&無頓着派なら「2個×12箱=24個」と書けます(そもそもこのスタイルであれば,箱のかけ算も,「3箱×4箱=12箱」となります).総合式は,「2個×(3×4)=24個」または「2個×(3箱×4箱)=24個」です.
数教協スタイルも,やってみましょう.「3×4=12」とするための,箱の数を計算式ですが,「3箱/列×4列=12箱」です.「2×12=24」については,「2個/箱×12箱=24箱」です.総合式は「2個/箱×(3箱/列×4列)=24個」で,カッコを取り除いてみると「2個/箱×3箱/列×4列=24個」となります.
単位を付けた式を書くなかで,いくつかずるい操作をしていますが,小学校では式の中に単位を付けないこともあり,問題にはなりません.3つの数のかけ算をする際に,どの順番で,2項演算としてのかけ算をするかにより,図にしたように途中段階が異なるのですが,最終的な計算結果は一致する,というのは(乗法の)結合法則と呼ばれるものです.
元ネタとさせていただいたブログの記事について,ちょっと書いておきますと,
- 「3項以上の掛け算」と,「掛け算の順序を守るべき」というテーゼは,無関係です.もし関連づけようとするなら,式で表す中に単位を入れることが求められます.それは結局のところ「大人のトーク」であり,今の小学校の教育に反映させることが困難となります.
- ある場面設定において「a×b×c」という式を立て,それを計算するにあたり,「(a×b)×c」と「a×(b×c)」の違いは何かというと,「a×bとはどんな数量を表すのか」と「b×cはどんな数量を表すのか」の違いと言えます.そして上で図にしたように,まったく異なります.これは「a+b+c」としたときに,「a+b」「b+c」がそれぞれ表すもの(それぞれの違い)にない特徴であり,したがって指導において配慮が必要と思われます.
- コメントを書きながら考えたことですが,総合式が与えられたとき,それと等価な「分解式の並び(系列)」の存在は,数学的帰納法*3で証明できます.証明自体は「大人のトーク」ですが,その証明をもとに,総合式に対する解析木(構文木)を作ることができます.名称はともかくとしてその図の作成は小学生が学習する四則演算においても可能です.そして,総合式を読み取り,どのような順序で計算をすればいいか(乗除が加減に優先する場合を含めて)の理解や指導にも,役立ちそうです.
解析木について,今回考えたケースでどうなるかを示します.


最後に,今回の図の作成コマンドを記します.
convert -size 160x120 xc:white -stroke blue -strokewidth 2 -fill none -draw "rectangle 1,1 40,40" -stroke none -strokewidth 0 -fill red -draw "rectangle 10,10 16,16" -draw "rectangle 23,23 29,29" 4_1.png
convert -size 160x120 xc:white -stroke blue -strokewidth 2 -fill none -draw "rectangle 1,1 40,40 rectangle 1,40 40,80 rectangle 1,80 40,118" -stroke none -strokewidth 0 -fill red -draw "rectangle 10,10 16,16 rectangle 23,23 29,29 rectangle 10,50 16,56 rectangle 23,63 29,69 rectangle 10,90 16,96 rectangle 23,103 29,109" 4_2.png
convert -size 160x120 xc:white -stroke blue -strokewidth 2 -fill none -draw "rectangle 1,1 40,40 rectangle 1,40 40,80 rectangle 1,80 40,118 rectangle 40,1 80,40 rectangle 40,40 80,80 rectangle 40,80 80,118 rectangle 80,1 120,40 rectangle 80,40 120,80 rectangle 80,80 120,118 rectangle 120,1 158,40 rectangle 120,40 158,80 rectangle 120,80 158,118" 4_3.png
convert 4_3.png -stroke none -strokewidth 0 -fill red -draw "rectangle 10,10 16,16 rectangle 23,23 29,29 rectangle 10,50 16,56 rectangle 23,63 29,69 rectangle 10,90 16,96 rectangle 23,103 29,109 rectangle 50,10 56,16 rectangle 63,23 69,29 rectangle 50,50 56,56 rectangle 63,63 69,69 rectangle 50,90 56,96 rectangle 63,103 69,109 rectangle 90,10 96,16 rectangle 103,23 109,29 rectangle 90,50 96,56 rectangle 103,63 109,69 rectangle 90,90 96,96 rectangle 103,103 109,109 rectangle 130,10 136,16 rectangle 143,23 149,29 rectangle 130,50 136,56 rectangle 143,63 149,69 rectangle 130,90 136,96 rectangle 143,103 149,109" 4_4.png
$ FONT=/cygdrive/c/Windows/Fonts/VL-Gothic-Regular.ttf
$ convert -size 160x120 xc:white -fill blue -pointsize 20 -font $FONT -draw 'text 45,20 "(2x3)x4" text 35,65 "2x3" text 110,65 "4" text 20,110 "2" text 70,110 "3"' -fill none -stroke blue -strokewidth 2 -draw "line 80,26 55,45 line 80,26 105,45 line 50,68 28,89 line 50,68 72,89" tree23_4.png
$ FONT=/cygdrive/c/Windows/Fonts/VL-Gothic-Regular.ttf
$ convert -size 160x120 xc:white -fill blue -pointsize 20 -font $FONT -draw 'text 45,20 "2x(3x4)" text 100,65 "3x4" text 40,65 "2" text 85,110 "3" text 135,110 "4"' -fill none -stroke blue -strokewidth 2 -draw "line 80,26 55,45 line 80,26 105,45 line 115,68 93,89 line 115,68 137,89" tree2_34.png
本日の成果
図を描くのに,これまでPowerPointかInkScapeを用いていましたが,今回はすべて,ImageMagickのconvertコマンドで作りました.配置を,実行コマンドで表現できるので,データ量を少なくすることができるほか,再現性,拡張性*4に優れていることに,気づきました.
その分,乗法の意味理解(かけ算の順序論争)への貢献は,控えめでした.


