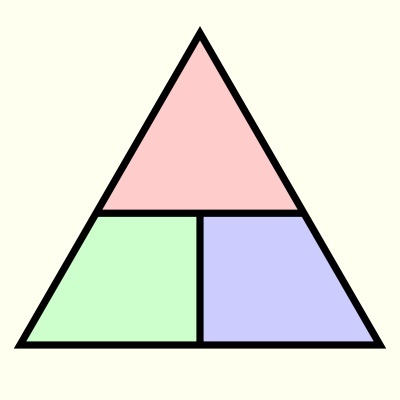
いきなりですが問題です．
正三角形があるとき，次のように2本の線分によって3つに分割し，それらの面積が等しくなるようにしたい．どのようにして分割すればよいか，答えなさい．
どこかから取ってきたというのではなく，オリジナルの出題です．
を見て，中学生向けの作図問題になりそうと思ったのでした．
点を明示して，問題文を書き換えてみます．
正三角形ABCがあるとき，次の条件をすべて満たすよう，定規とコンパスを使って，線分DEおよび線分FGを作図しなさい．
- 辺AB上に点D，辺AC上に点E，辺BC上に点F，線分DE上に点Gがある．
- DEはBCに平行であり（DE‖BC），FGはBCに垂直である（FG⊥BC）．
- △ADE，四角形BFGD，四角形CFGEの面積はいずれも等しい．
といったところで解答です．
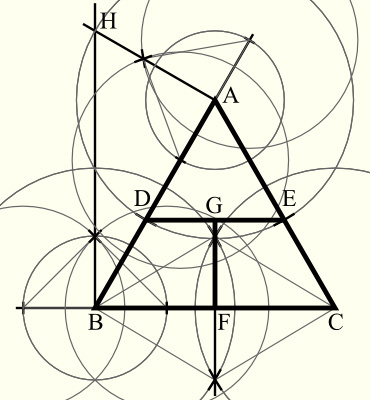
Aを通るABの垂線と，Bを通るBCの垂線を引き，その交点をHとします．
Aを中心として，AHを半径とする円を描き，そのABとの交点をD，ACとの交点をEとします．
BCの垂直二等分線を引き，そのBCとの交点をF，DEとの交点をGとします．以上です．
これで面積が等しくなる理由を書いておきます．まず△ABHは，∠BAH＝90°，∠ABH＝30°，∠AHB＝60°の直角三角形で，AH：AB＝1：√3であり，ここからAH＝(1/√3)ABを得ます．そしてAH＝AD＝AEです．
また△ADE∽△ABCであり，その相似比はAD：AB＝(1/√3)：1なので，面積比は(1/3)：1となります．したがって△ADE＝(1/3)△ABCです．それと，∠ADE＝∠ABCと同位角の性質から，DE‖BCといえます．
四角形BCED＝△ABC−△ADE＝(2/3)△ABCであり，上の手順で作図した四角形BFGD，四角形CFGEは合同なので，面積は等しいといえます*1．四角形BCED＝四角形BFGD＋四角形CFGE，四角形BFGD＝四角形CFGEから，四角形BFGD＝四角形CFGE＝(1/3)△ABC＝△ADEとなります．
2つの画像は，SVGでつくりました．座標計算・画像生成のRubyスクリプトは，Gistにて公開しています．
（最終更新日時：Mon Oct 22 06:02:28 2012ごろ）
*1:四角形の合同の証明は，学校で出てきませんね．代わりに，ABF≡△ACF，△ADG≡△AEG，四角形BFGD＝△ABF−△ADG，四角形CFGE＝△ACF−△AEGで説明ができます．
