[http://togetter.com/li/425746:title]でつけたコメントと，書けなかったことを，Q&A形式にして整理しました．2012-12-26 朝に，転載を増やすなどいくつか修正しました．
Q: 「立式」って何?
A: 「式を立てること」「式に表すこと」なのでしょう．
小学校学習指導要領解説 算数編では，p.128が最初の出現で，他にも何度か出現します．いずれにも定義がついていないので，教師は知っていて当然なのかもしれません．
なお『算数教育指導用語辞典』の索引には，見つかりませんでした．
Q: 文部省の指導要領では、「5人に1つずつ配ると5個必要」を単位と見なして5[個/巡]x4[巡]と立式することを禁じていないでしょ?
A: 「配ること」を児童が発想したり，先生が誘導したりする授業例があればいいけど、見かけるのは「配るの禁止」のほうです（365日の算数学習指導案 1・2年編 p.66，りんごのかけ算）．
なお，「かけ算の順序論争」がWebで容易にアクセスできるようになった現在では，「配ること」に基づく考え方を子どもが出すと，先生は「素晴らしい発想」ではなく，「入れ知恵か」と思われるかもしれませんね．
Q: 式に4個×5人と単位とともに書かせればすむのでは?
A: 積の数量は，何になるでしょうか．「4個×5人＝20個」「4個×5人＝20人」「4個×5人＝20個人」があり得るのですが．Vergnaudも，"it is not clear why 4 cakes × 15 cents yields cents and not cakes"と指摘しています．
そして「4個×5人＝20個」「5人×4個＝20個」という判断を，学習者（児童）ができるようになるには，どのような学習が必要でしょうか．コストをかけただけの効果を，示すことはできるでしょうか．別のところで，都合の悪いことが起こらない（起こるとしても小さくできる）ような，保証はあるでしょうか．
Q: その生徒がどういう風に考えているのか判断する解決法を挙げてもらえませんか?
A: 手法の一つに「作問」があります．出題する側は，「8×4」といった，かけ算の式を提示します．子どもたちは，その式になるような文章題を作ります．
かけ算の式と，子どもが設定した場面（文章題，絵など）を子ども自身が照合し，合っていないと認識する話が，算数教育の団体で活動する先生方の本に，書かれています．
学会の解説のほか，いわゆる非順序派の出題などを含め，算数教育に関わる各団体は，かけ算の順序についてどのような見解を出していますか?で整理していますので，ご覧ください．
Q: 5×4にせよ，4×5にせよ，後ろの数字を「かける数」でいいのですか? もしかして，「かける数・かけられる数」というモノ自体がナンセンス？
A: 学習指導要領解説から取ってくると，「乗数や除数が整数の場合の小数の乗法，除法」という中に「例えば，0.1×3ならば，0.1＋0.1＋0.1の意味である」(p.142)とあります。この3は乗数すなわちかける数でないと、話が通りません．多くの本や解説から，算数教育において×の後ろが「かける数」なのが確認できます．
ところで，「乗数が整数の場合の小数の乗法」は，「かける数・かけられる数」の区別の必要性を示唆しています．例えば「2.4cmの紐が7本」という状況を作るのは，2つの数を交換した「7cmの紐が2.4本」よりも簡単です．当ブログで「同等の量」と書いてきたグループの問題と深い関係があり，そこでは，かけられる数とかけ算の答えが「量」あるいは連続量，かける数が「個数」あるいは分離量となります．小学校では，同等の量に関する場面のうち，量も個数も整数になるものを3年で，量が小数，個数が整数になるものを4年で，量が分数，個数が整数になるものを5年で学習し，小数の乗法（5年），分数の乗法（6年）と分けています．中学だとか科学だとかを持ち出す前に，こういった小学校の学習のステップにも，注意を払ってもらえればと願います．
「乗数と被乗数を交換しても積は同じになる」(p.88)というときの乗数・被乗数が何になるのかは，「×」から学んだこと・2012年秋冬モデルの「乗数と被乗数を交換したら，どうなるの?」をご確認ください．
Q: 「玉川の何かの本」って何?
A: 『小学校指導法 算数 (教科指導法シリーズ)』のことです．
かけ算に関する主要なところは，次のとおりです．
乗法の場面、「1ふくろにミカンが3こずつ入っています。5ふくろでは、ミカンは何こでしょう。」は、3×5と立式される。立式は、「1つ分の数×いくつ分＝全体の数」とまとめられ、それぞれ被乗数、乗数という。ところで、「オリンピックの400メートルリレー」や「このDVDは16倍速で記録できる」、「xのk倍は」の式は、どのように表わされるであろうか。それぞれ、一般的には「4×100mリレー」、「16×」、「kx」と表される。被乗数と乗数の位置が教科書の書き方と逆になっていることに気付くであろう。この例から分かるように、乗法では、数の位置ではなく、数が意味する内容に注目して、どの数が1つ分の数であるか、いくつ分はどの数かをしっかりと読み取ることが大切である。第2学年や第3学年では、読み取った数を、「1つ分の数×いくつ分＝全体の数」と表現できることが重要であり、逆に、この立式ができているかで、数の読み取りができているかを判断できる。しかし、高学年になり、乗法では交換法則が成り立つことや外国での立式を知り、数の意味をしっかり理解できていれば、必ずしも第2学年で学んだ順序で立式することを強制しなくてもよい。
（『小学校指導法 算数』pp.91-92）
Q: かけ算で答えを出させてから，「もうひとつ分あるといくつになるでしょう」的な問題が出せませんか?
A: 「もうひとつ分あるといくつになるでしょう」的な問題は、問題集で見かけましたが手元に良いものが見当たらないので，代わりに…
『活用力・思考力・表現力を育てる!365日の算数学習指導案 1・2年編』p.107では，1パック6個入りのヨーグルトが，1パック，2パック…と順に増えたとき，ヨーグルト個数がいくつになるか，というのを学習指導案にしています．
なお，かけられる数が1増える場合と，かける数が1増える場合とで話が違ってくるのは，(a＋1)×b＝a×b＋bにて検討しています．
Q: 「個」や「人」は単なる数詞であって「単位」ではないんだってばさ。掛け算すればもちろん単位同士だって掛け算されます。掛け算において「直積モデルがダメ」な場合なんてあるわけない。
A: 3つの文に対して，一つひとつ回答します．
- 混み具合を表す「人/m^2」や「m^2/人」を「単位」とするためには，「人は単なる数詞」という解釈のままでは難しいように思います*1．
- 単位のかけ算は，「4個×5人＝20個人」（と子どもが理解してしまうこと）を想像すると，賛同できません．
- 直積やそれと同種のものによるかけ算の意味づけでは教育上まずいことが，国内外で指摘されておりまして，かけ算には本来，順序がないで取りまとめました．
Q: 指導要領の記述が「後ろは乗数」の流儀に統一されているのは分かったけど，「後ろは乗数でなければならない」と読むのは教条主義的というか原理主義的というか，あまりに硬直した姿勢では?
A: 「後ろは乗数」の件は結局「小学校のルール」ですかね．そうでない表記を，日常生活の中から2つ，算数の解説から1つ，以下に示します．
- ふせんの「2色×60枚」は，小学校のルールでは60×2でしょう．
- 15ピース×600円は，「×」を使っているけれども，かけ算ではない例です．しかしこう書きたい心情は分かります．
- 乗数が内包量に載せた
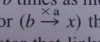は，「a×b＝x」の解釈の一つです．
かけ算の順序論争に関わるということは，この種の泥臭い話にどこまで関わり，新たな情報をどう取り入れ，知識として蓄積していくかということだと，思っています．
Q: 掛け算は5[個/人]×4[人]が正しいんじゃないのかな? 4[人]×5[個/人]でもいいはずでしょ?
A: 「5[個/人]×4[人]」は「これが正しい」ではなく，一つの考え方と見るべきでしょう．数学教育協議会（数教協），学力の基礎をきたえどの子も伸ばす研究会（学力研）あたりの流儀です．教科書にも，海外文献*2にもなく，また「4[人]×5[個/人]」は上記団体でも，採用されているのを見たことがありません．
「一つの」というのは，他の考え方もあるからです．「4個×5人」は，「4個/人×5人」のほかに，「4個×5」のように，かける数の単位が抜けて「〜倍」扱いとすることもできます．その場合，「5×4」という答案は，「5人×4個＝5人×4＝20人」と解釈されます．
「4個×5人＝20個」「4個×5＝20個」はサンドイッチと呼ばれ，よく非難の対象となっていますが，累加との相性が良く，かけられる数が小数・分数でも，かける数が整数ならたし算で表せるというメリットがあるほか，算数教育や数学の実績・根拠もあります．サンドイッチはくだらない・2012年8月バージョン(1/2)，かけ算のサンドイッチをご覧ください．
「正しい」ではなく「一つの考え方」としたのは，それは信念の話だからです．そしてパー書きの単位は，かけ算で表される多様な場面を記述するには，十分ではありません．
私の理解・信念を書いておくと，「5人に4個ずつ」と「4cmの5倍」と「5人が4時間働く」は，異なる種類のかけ算の考え方（構造，モデル）です．「4cmの5倍」の4cmをパー書きの単位に変換するのは不自然で，実際，数教協でも「倍概念」として別扱いにしています．
という信念はあるものの，3つのモデルを平等に，小学校で扱えというわけでもありません．それらを，より多くの小学生がそれなりに理解してくれる（4個×5人＝20人にならないことを含めて）には，累加と拡張に基づく現行の指導法に賛成，アレイモデルに到底賛成できない，「1あたり」にはやや反対，といったところです．
Q: 「5人が4時間働く」って，何でそんなのが出てくるのですか?
A: これは仕事算と関係する話です．電力と時間をかけ合わせて電力量を得る，というのは小学校で利用できないので，別の事例で説明した次第です．*3
時間と人のかけ算は，4マス関係表で少し取り上げています．日数と人数のかけ算は，「3日間欠席した人が2人いれば，2×3＝6で，のべ6人欠席です。」「逆に，3×2＝6のように，日数をもとにして考えると，のべ6日欠席です。」（「のべ人数」って，どんなことなの；対象を，広げる，狭める（4. のべ）より孫引き）とのことです．
Q: 状況が「５人に飴を４個ずつ配る」と言ってるのに「５×４」を見て「5人×4＝20人」と「解釈」するのは単なる馬鹿者では?
A: 指導例は，昭和26年の学習指導要領試案に見られます（以下は，かけ算の順序問題がWikipediaにからの転載です）．
三年の乗法九々の学習で，三の段がひととおりすんで，こどもたちは三の段の九々がすらすら唱えられるようになった。そこで，教師は次のようなテストを行って，こどもがかけ算の意味を理解して，九々を適用する力が伸びたかどうかを調べてみた。
問題 ３人のこどもに，えんぴつを２本ずつあげようと思います。えんぴつがなん本いるでしょう。どんな九々をつかえばわかりますか。
どんな九々をつかうかという問に対して，３×２＝６と答えたものが予想以上に多いことがわかった。これによってこどもは問題に出てくる数を，その数の意味を深く考えもしないで，出てくる順に書き並べ，その間に，かけ算記号を書き入れることがわかった。問題に出てくる数を頭の中にいったん収めて，演算の決定に導くように問題の場を組織だてる力が欠けているらしいことがわかった。そこで，その欠けていることについての再指導に入るわけである。
V. 算数についての評価
３は人数を表わしている数である。それを２倍した答の６は何といったらよいか尋ねてみる。それで，６人となって問題の要求に合わないことを説明する。このようにして３×２＝６とするのが誤であることを明らかにしたとする。
しかし，上のような指導だけでは，問題をすこし変えてテストしてみると，ほとんど進歩しないことがはっきりわかってきた。つまり，一方を否定するような消極的な指導だけでは，前に述べたような問題を組織だてる力を伸ばすのに，ほとんど役だたないことがわかった。これが再指導に対しての評価であって，指導の方法を修正する必要をつかんだわけである。そこで；問題解決を，同数累加の形にもどして，倍の概念をしっかり押えるように指導したのである。今度は成功した。この事実を教師が見届けたのもやはり評価である。
平成になってからの事例もあります．『板書で見る全単元・全時間の授業のすべて 小学校算数2年〈下〉』pp.46-47（「2×8ならタコ2本足」を振り返る）の，次の図です．
「５人に飴を４個ずつ配る」に対する「５×４」は，「それだと20人と思われちゃうよ（君がそうじゃないという明確な意図をもって書いたとしても）」です．書いた人がどう考えたかよりも，「そう書いたらどう受け取られるか」に注意をしたいところです．
Q: 掛け算の順序は，「ローカルルール」なんでしょ? そんなものを一般的なルールとして教えるとしたらそれは「嘘」だと思います。
A: 「ローカルルール」と言う人の中で，日本国外はどうなっているかを説明してくれる人がいないのが残念です．
自分が読んできた英語のかけ算指導の文章は，純粋な数のかけ算はどっちでもいいけど，数量が絡む話は区別・配慮が必要というものばかりです（かけ算には本来，順序がない，Luckier!）．交換法則が成り立つから，数量が絡む話（具体的な場面）でもどっちでもいい，と主張する本は見かけません．
そういった区別・配慮が必要と認識できたら（認識できなかったら，ここでさようならとしたほうがお互い良いように思います），それをどのように実現するか，そのためのルールはどの範囲で利用可能なのかを詰めていくことになると思っています．
Q: 「単位も掛けられる」「順番を変えてもそれは同じ」と言う事を言いたいだけです
A: 大人の世界でそれを言う分にはいいのだけれど，小学校の算数で認めてもらおうとするならば，単位の扱いをもっと精密化すべきでしょう．小学校の先生方が利用可能な文書やノウハウとして取りまとめ，授業で試用してもらって高評価を得て，全国へ展開していければ，教科書や学習指導要領に載る（関連：算数ものづくり）のも，夢物語ではありません．
先生方へのサポートになっていると言うには，おこがましいですが，私がとりまとめた中でアレイ図，包含除と等分除 再考，「かけ算指導案」をお探しの方へは，教育機関ドメインからのアクセスがかなりあります．ある論文を紹介したところ，その著者からメールをいただいた経験も，当ブログの維持を支えています．
「順番を変えてもそれは同じ」とのことですが，15ピース×600円という反例にも気をかけてもらえればと思います．
Q: 小学校でそのルールを使用すべきとする学術（数学・算数）的な根拠はあるのでしょうか?
A: 学術（数学・算数）面で探るなら、中島：乗法の意味についての論争と問題点についての考察（以下「中島論文」）をおすすめします．
米国での議論を紹介したあと，日本の算数ではどう指導しているかを解説しています．日本は被乗数×乗数で一貫しており，英語では乗数×被乗数が基本だけど，被乗数×乗数もあるなあとなっています．昨日のエントリで取り上げたAnghileri & Johnsonの解説も，両方を使っているように見えます．
中島論文は，遠山啓がトランプ配りを含む記事を出した（1972年）のよりも前である一方で，その論旨が2010年の年末に刊行された『数学教育学研究ハンドブック』の「乗法・除法の意味づけ」(pp.74-75)で，次のように引き継がれています（日本数学教育学会による，乗法の意味づけからの転載です）．
これらの研究成果から，乗法・除法の意味づけにおいては，数学的な考え方の育成を目指す立場からは，割合による意味づけに教育的な価値がある。これは，整数は同数累加で導入し，乗数が小数になった段階で同数累加では意味づけられなくなる。そこで，被乗数，乗数の意味を（基準量）×（割合）と拡張し，これまでの整数の場合と同様に用いることができるようにすることである。数学的な考え方を育成するためには，意味の拡張は重要な指導の場となってくる。
高学年で学習する「割合」を考慮して，かけ算の導入を図っているというのは，今回の赤ペン先生のロジックとも重なっています．
中島論文はあいにくCiNiiからだと有料です．1968年の「被乗数×乗数」とアレイ図で一部引用しています．
それより前となると，「緑表紙教科書」に着目するのはいかがでしょうか．といっても，教科書そのもの（復刻版が出ています）ではなく，編集に関わった人による解説です．『「小学算術」の研究』という本が出ていて，緑表紙にアレイ図，筆算の順序で取り上げています．
Q: ローカルというのは地理的な話ではなく，算数教育とか小学校教育という意味です．それ以外の世界，例えば一般社会では逆でも構わないですよね?
A: 一般社会への話をするなら，物品の数量表記のかけ算は，その左が一つ分の数量，右が幾つ分になるのが圧倒的なのを，今年確認してきました．
この話において逆の場合というのは，12月20日付では「例外」，12月19日付では「反例」として，示しています．
そういった事例を意識して，「式をどう読めばいいのか」「どう書けば（かけられる数とかける数に何を書けば），誤解されずに伝わるか」にも，配慮できる子どもになってほしいと願っています．
Q: 組立単位を考えれば，「単位も掛けられるものである」が当然ですよね?
A: まず，組立単位を認めるか認めないかというのが一つの分岐点です．次に，組立単位は，式から，答えとなる一つの数量を得るのにはいいのですが，そのことは，場面と式との対応づけについて，何も言っていないので，その対応づけを支えるものが必要になります．算数教育では，組立単位を採用しておらず，その一方で後述のとおり，「式に表す」「式を読む」といった活動を通じて，学習者に何を身につけてほしいかについての見解がまとまっています．
ところで，「量は数（すう）と単位（または単位に準ずるもの）の積の形式で表せる」（wikipedia:量）という立場は，数学の「量の理論」のもとで共感できません．というのも，いわゆるゼロ量の取り扱いに，注意が必要だからです．ゼロ量を含むと，量の加法性のうち，任意の2つの量AとBに関してA＋B＞Aと言えないのです（なぜコメント凍結）．『量と数の理論 (1978年)』pp.26-27で記されているのですが，この本も入手困難と思われますので，0にかける，0をかけるへリンクしておきます．
Q: 「掛け算の順序」という用語の出自と妥当性は興味がありません．順序の出自と妥当性を問うています。
A: 用語や指導の出自はかけ算の順序の伝統でまとめています．
妥当性に関しては，「4つずつキャンディを持っている3人の子どもがいる」と「3つずつキャンディを持っている4人の子どもがいる」とは違う状況なのだから，算数を学習している段階で，式において別に書けるようにしたい，という欲求が起こるか否かの話のようにも思います．
Q: 後々に「順序は方便です」というような教育をされるのですか？
A: その方針では，どれだけWebで情報収集し，TwitterやTogetterで発言しても，教育に携わる人々には，届きそうにありませんね．
CiNii 論文 - 小学校児童による有理数の乗法における乗数効果の分析の論文は，オープンアクセス（無料）になっているので，ダウンロードしてご覧ください．そこでは「順序」ではなく，「〈乗数と被乗数が区別される文脈〉」という言葉が使用されています．それに相対するものは「面積などの〈乗数と被乗数を区別しない文脈〉」です*4．
〈乗数と被乗数が区別される文脈〉を「倍」，〈乗数と被乗数を区別しない文脈〉を「積」と略記したとき，日本の小学校では，加法（1年），減法（1年），除法（3年；包含除・等分除）と違って，乗法として出てくるのは「倍」が2年，「積」が4年（長方形の面積の公式）で，学年が異なります．「積」の離散的・視覚的構造であるアレイは，2年でも多く見られますが，アレイ「で」（「積」「で」）かけ算を理解するのではなく，アレイ「を」（「積」の中で，2年で取り扱えるもの「を」），「倍」に基づいて立式し*5，計算するという次第です．
低学年では「一つ分の大きさ×いくつ分」という最小のツールで可能な限り問題を解き，高学年では面積の公式のほか，数量関係などの知識を得て，活用していくことで，それぞれに応じた式の立て方，また式の読み方がなされます．数量関係と書きましたが，比例の表に着目すると，ある文章題の式が30×2とも2×30とも表せるという授業例を，2×30gで取り上げています．
あとは虚心坦懐に，多くの刊行物や---もしお金をかけるのが面倒でしたらここを起点に当ブログの関連記事を追いかけていただいて結構ですので---国内外の算数・数学教育においては，「順序」ではなく，「かけ算の意味」を意識して，授業や出題でどんな工夫がなされているか，また児童らの理解の状況はどうなっているか，その一端を知っていただければと願います．「順序」は，かけ算の話に限っても結合法則，乗除先行，九九学習など，複数の文脈で用いられており（かけ算の順序，計算の順序），「かけ算の順序論争」はそういった多様性に目を背けるという点でも，残念に感じています．
Q: 教科書出版社の言い分を右から左へ流しただけ?
A: いえ，算数教育を実践し，改善を図ろうとしている人々の間の共通見解，いわば通説と言ってもいいと思います．再掲になりますが，算数教育に関わる各団体は，かけ算の順序についてどのような見解を出していますか?をご覧ください．
Q: 式から児童の思考を正しく読み取れるのかどうか・・・
A: 直接的な回答は以下のとおり．
Q: 順序では，読み取りができているか判定できないのでは?
「×」から学んだこと・2012年秋冬モデル
A: 《りんごの問題》の類題は，先に書いたとおり，いくつかの教科書に掲載されています．市販の問題集からも，見つけることができます．市販されていないドリルにも，きっとあるのでしょう．
論争の対象となっている文章題は，かけられる数とかける数との区別を授業で学習した上で，「一つ分の大きさ」と「いくつ分」を読み取り，かけ算の式で表すという知識・技能が，きちんと定着したかを測るために出されたと理解するのがよさそうです．
この出題は，学習中であれば形成的評価，単元や学年のまとめであれば総括的評価に，それぞれ関連します．
また3年になり，わり算またはより広い範囲のかけ算を学習する前に，2年のかけ算の理解度をチェックする際の出題（レディネステスト）も見られ，これは診断的評価です．
ただし，「教育評価」の話を知っておくことが前提です．「評価」で上の記事を検索すると，いくつかヒットすると思います．本としては『教育評価 (岩波テキストブックス)』がお勧めです．当ブログでは教育評価，2冊目，評価と設計で書いています．診断的評価・形成的評価・総括的評価の3点セットは，私自身，データベースの概念設計・論理設計・物理設計の3点セットを照らし合わせることで，理解が容易になったのでした．
ところで上記引用は，かけられる数とかける数とを区別しない考え方（いわゆる「非順序派」）に基づく授業をしてはならないとは，言っていない点にも注意してください．そういった指導をする際には，関連する単元・学習内容や前後の学年まで考慮に入れた授業計画や学習指導案の作成，そしてそのもとでの実施・評価が不可欠です．そういった実績が見当たらない限り，絵に描いた餅です．
もう一つの注意点は「式の読み取り」でしょう．これについては，『数学教育学研究ハンドブック』の第3章§3が「文字式」がこの業界の見解であり，理解を深めていくための糸口になっています．中学数学で使用する文字式のほか，具体的な整数値を擬変数（“いろいろな数の代表”）として扱えるという話も入っており，2年のかけ算にも関わりがある内容です．
主要な部分を書き出します．
文字式の利用過程を詳しくみると，事象を数理的に捉えて文字式で表す過程が「式に表す」過程であり，文字式から事象の特徴を解釈する過程が「式をよむ」である。「式に表す」と「式をよむ」は表裏一体となっている。
一方，文字式は他の言語と異なり，表現された式を一定の規約に従って形式的に変形することができるという優れた機能をもっている。「式の形式的処理」の過程は，「記号」と「記号」の結合の仕方が問題となり，言語学では統辞論の分野である。文字式の変形は，もとの事象へのより深い考察を可能にする。なぜなら，変形の結果として得られた文字式を解釈・評価・比較することで，すなわち「式をよむ」ことで，もとの事象に対して以前とは異なる洞察が可能となるからである。図2ではこの過程が「読む」と明記されている。
ここで重要なのは，図1，図2では顕在化されていないが，「式に表す」から「式の形式的処理」，そしてその結果の解釈としての「式をよむ」という過程は，一度だけではなく，場合によっては何度か繰り返されるという点である。そのことにより，事象の特徴や一般性が次第に明らかになる文字式は数学における表現と伝達の手段だけでなく，思考の手段として際立った価値をもっているのである。
文字式を使用する過程を「式に表す」「式をよむ」「式の形式的処理」としたが，これらは当然のことながら密接に関連している。したがって，先行研究においてもこれらが混在して出現するだろうが，どこに主として焦点が当たっているかで分類整理することにする。
(pp.83-84)
図がなくても，「式に表す」「式をよむ」「式の形式的処理」の関連づけは想像できると思いますが，もし困難でしたら，本をご覧ください．
他にも，算数教育の実態を知るのに有用なとりまとめが，この本でなされています．乗法の意味は，その直前のセクションです．「順序ありの指導が良いとするエビデンスがほしい」という主張には，まず通説に対抗する側が，順序なしのほうが良いとするエビデンスを出す必要があることに留意した上で，第1章§2（研究方法論）を通じて，定量評価（量的研究方法）への限界を知っておいてください．国内外の状況などは，第6章に書かれています．
そういった蓄積と比較しながら，あなたの「式の見方」「教育への関わり」を見つめ直すというわけには，いかないものでしょうか．
Q: 特定のコメントはスルーですか?
A: まあ，自分の知っている情報のもとで答えられるところだけですね．
…と思ってTogetterのところを見直したら，大物をスルーしているのに気づきました．関連するのは，これかな：
ネット上では、順序不要の意見が大勢を占めており、また『かけ算には順序がないのか』という書籍も出版されていますが、歯切れがよくて威勢がいいものの、数学教育学に関する国内外の動向を十分に踏まえていないように感じます。主張はそれなりに明快なのですが、学校にその考えを普及させるための具体的・現実的な行動が見当たらない点も、残念に思います。（ここの項目は、http://ishiba-shigeru.cocolog-nifty.com/blog/2008/11/post-8451.htmlの記述を一部使用しています。）
トップページ - 「×」から学んだこと@wiki - アットウィキ
Q: 掛け算という計算をいったん教えたら「具体的なモデル」からは自由にしたいです
A: 賛成です．とはいうものの，計算の仕方を忘れてしまったときに，「具体的なモデル」に戻って復習できるようにしてほしいですし，そこは「してほしい」と他人事にせず，学校の外で，我々が関わる余地があるようにも思います．
それと別に，「自由」という言葉が「答えが出れば，手段・理由は何でもいい」とならないか，という不安もあります．学校はどうなっているらしいかというと，学習指導要領の改訂で言語活動・算数的活動の充実が求められ，とくに授業では，立てた式がなぜそうなるのかを本人が説明したり，他の子が説明したりするものが増えているそうです．
こう書いてみると，手間が増えて世知辛いようにも見えますが，飴の出題には「5×4＝20でも理由は言えるけど、マルバツをつけるのは先生だから、4×5＝20にしよう」と，複数の候補を思いついた上で，比較して一つの答えを決めることができる子になってほしいという願い（管理者紹介 - 「×」から学んだこと@wiki - アットウィキ，余談で話す）は，維持することにします．
Q: だから、一冊の本の中である流儀に固定して書いてあっても全然おかしくない（というか普通）でしょうが、それが墨守すべき「定義」であって逆順は間違い、って考えはおかしいでしょ、と言ってるんですけど…。その答えが「世間一般でもそうしてある事が多い！（キリッ）」ですか。はぁ。
A: 「墨守」「定義」「逆順」といった言葉は，算数・数学教育の書籍や学習指導案で見てきた語彙と，水と油の関係です．なので，研究や実践の蓄積と異なる方向を向いて主張をしたいと理解しました．
まあそれはそれでいいんじゃないでしょうか．「教育」というカテゴリの外で，くだを巻くのであれば．共感者もいるようですし．
もし教育を本気で変えたいのなら，「変える」以前に現状をきちんと「観察する」ことが不可欠です．教育学部に入るか，良い師匠について学ぶのを，考えるべきでしょう．そこまで極端に走らなくても，テーマを決めて集中的に情報収集を行い，分析することは，学生だろうと働いていようと誰だって（時間と意欲があれば）できる，観察の活動です．
Q: 掛け算の順序を定義づけたものは無いと言う事でよろしいですか？
A: まず，「掛け算の順序」を語っているところ，人々にその定義を確認しましたか? 『かけ算には順序があるのか (岩波科学ライブラリー)』では，どのように定義されていますか?
私自身は，乗法の意味，情報の価値を書いたのをきっかけに，「順序」という言葉は不適切と認識しています．
定義を私のほか，教育に携わっている人々に求めるのではなく，批判している人々の考え方や，その対象となっている授業・問題などを観察し，得られた知見を言葉にするというのは，できないものでしょうか．その際，かけ算の問題の構造をご確認いただければと思います．「構造」という言葉の使われ方が気になり，整理したのでした．
とはいえ，教育関係者が「かけ算の順序」を書いているものを知っています．以下，そのうち2つを紹介します．
一つは，wikipedia:かけ算の順序問題の外部リンクにも入っている，北海道教育大学の教授 宮下英明による論考です．定義は，例えば積の立式の論理にあります．低学年の出題はその図式のみでよく，「速さ×時間＝道のり」になると，ここにあるように，比例関係を活用します．きちんと理解するには，上記2つだけでなく，そこのサイトの文章を手広く読むこと*6，そして数学の素養も必要です．個人的に読んできた「量の理論」とある程度重なっているので，切り捨てるには惜しいコンテンツです．
もう一つは，2002年に書かれた，国際協力事業団の報告書です．このページに「かけ算の順序」という言葉が入っています．しかし，定義がなされているわけではなく，日本語・英語・タイ語のそれぞれで，かけ算を「言葉」と「式」で表す際の，かけられる数・かける数の順序に注意して，カリキュラム開発をすべきだと述べています．それぞれの順序は決まっている，と読むことができます．この件は，文献：馬場2002として読んだ記録を残しています．
Q: 一般には必ずしも適用できないと言う事を後に教えるのか?
A: 「一般には必ずしも適用できないと言う事を後に教える」とのことですが，適用できなくなるため，かけ算の意味の拡張を図る話には有名なものがあって，具体的には5年，かける数が小数になった場合です．これは割合の計算で出てきます（またここでも，赤ペン先生の回答とつながります）．
もし，「（1つ分の数）×（いくつ分）＝（全部の数）」が，一般には必ずしも適用できない，という意味で書いたのなら，おそらくこの式の能力を過小評価されています．まず実用の面でいうと，物品とりわけ食品や生活用品の数量表記は「（1つ分の数）×（いくつ分）」に当てはめれば，全体の数が書かれていなくてもその単位が推測できるし，書く際にもそうすればいい（誤解を少なくできる），というコミュニケーションの恩恵をもたらしてくれます．
「能力」というのは，「倍」と「積」から学んだことで書いた言葉を使うと，《倍指向》と《積指向》が同等である，ということです．《積の乗法》は《倍の乗法》に帰着することができます（その逆も）．そうするとあとは，《倍指向》と《積指向》のいずれで導入すればいいのか，比較検討する流れになって，《積指向》の問題点の（出典付きの）指摘へと到ります．
別の言い方をすると，「（1つ分の数）×（いくつ分）＝（全部の数）」では長さ×長さ＝面積が言えないよというのが批判者，それに対して単位正方形の個数を求めればいいじゃないかとして長方形の面積の公式を得るのが学校教育です*7．
Q: かけ算の順序論争は，交換法則を認めるか認めないかの論争ですか?
A: ええ，それは一つの切り口だと思います．そしてそうすると，交換法則を適切に定義し，それが小学校の算数において（必要なら，普段の生活や科学などへの活用も含めて），どこで適用可能かを同定すればよい，となります．
海外の解説や，国内の解説・出題例を総合すると，無制限に乗法の交換法則は適用できないこと，言い換えると「4×5と5×4の答えは同じ．だけど意味は違う」は，確定と言っていいと思います．意味の違いについて，英語文献を2つ挙げます．一つは，Luckier!で引用した練習問題です．もう一つは資料が主，判断が従（1. 乗数効果）に書いた調査事例です．学年が上がり，小数を含むかけ算・わり算を学習したあと，「毎秒16マイル，0.85秒でどれだけ進む?」に対してかけ算を選ぶ子どもは，「毎秒0.85マイル，16秒でどれだけ進む」の場合よりも少ない（大人から見れば，その道のりは「16と0.85をかけたらいい」のだけれど）ことが示されています．
「交換法則を適用すればどちらでもいい」に賛意を示せない理由の一つは，こういった出題や調査の記載，またそこに到るまでの人々の創意工夫や子どもたちの行動・反応を---国内外を含め---ないがしろにしているように見える点にあります．
Q: 外国で，かけ算の順序が反対だとバツにする事例はありましたか?
A: 答えとしては，次の2点です．(1)事例は見つかっていません．見られない（探す必要がない）理由は，言語・文化・教育を背景として説明ができます．(2)「a×bとb×a（5×6と6×5）が同じでないような，日常生活の例を挙げなさい」という出題がありました．
今回の質問文は，「倍」と「積」から学んだことの20と同一です．そこではブラジルの件，16×0.85の件を挙げましたが，その後も，質問に該当するような出題例は，見つかっていません．
幸いにもその理由を推測できる文献を，発見できました．Anghileriらによるもので，そのうち鍵を握る記述は，次の2点です（Luckier!）．
- "Give some real-life examples of situations in which a multiplication product a×b (for example, 5×6) is not the same as b×a (6×5)."という練習問題が入っていること．
- 「"3 multiplied by 4"」と「"3 times 4,"と"3 fours."」とに分けて，後者のみを詳しく説明していること．
1番目の項目から，日常生活への適用において，5×6と6×5は違う場合があること（を著者らが認識していること）が確認できます．交換法則を解説している他のページと合わせて，5×6と6×5は意味が違う（交換法則を適用して「同じ」とできるのは純粋な数に関してだけ）と理解できます．練習問題はその本の読者すなわち研究者・教師・教師を目指す学生向けですが，「a×b」「b×a」を取り除いて，かけ算を学習中の小学生にやらせてみるのは，困難ではありません．
2番目の項目から読み取れるのは，英語圏では，3×4に「3に4をかける」と「3を4にかける」の両方の解釈・運用があり得ることです．この件は，中島健三が次のとおり（1968年に）注意書きを述べています．
4) 4×2は，英語ではfour times twoまたはfour twosなどという関係で，乗数と被乗数がわが国の場合と反対になっている．
8) 以下では，乗数，被乗数の順については，わが国の表記による．
9) (略)なお，註4)で，アメリカでは，乗数を先にかくとのべたが，最近では，わが国の場合のように，乗数をあとにかく方法（乗数をoperatorとしてみる場合に統一的にでき便利である）をかなり取り入れるくふうがされている．この場合，3×4は3 multiplied by 4などと呼んでいる．
（「乗法の意味についての論争と問題点についての考察」p.77；1968年の「被乗数×乗数」より孫引き）
こういったことを考慮すると，英語圏では3×4の意味が日本と反対であっても，英語のこの種の本を読む，おそらく欧米の研究者や現職教師らの間で，3×4を「3を4にかける」といった，一つの意味で教えるような授業を作ろうというのが，不自然に思えてきます．決まった順序で書かないとバツにするような出題が見当たらないのは，そこからの論理的な帰結となります．
2つの項目を組み合わせると，次のことが言えます．式の解釈としては「どちらもあり得る」けれども，1番目の項目としてあげた練習問題は，かけ算の式の意味を教室で共有（または解答者が設定）すれば，出題ができます．一人の子どもが，5×6の場面例と，6×5の場面例をそれぞれ答えれば，他の人がチェックすることも可能です．「それぞれ反対だよ」という指摘もあり得まして，そういった流れが，ブラジルのサイコロの話に結びつくようにも思います．
さて，日本，我々の教育環境にも目を向けましょう．かけ算については戦前から，「3×4」と書いたら「3に4をかける」であり，3がかけられる数，4がかける数で一貫しています．
それに加えて，授業研究その他を通じて教員間のネットワークが充実しており，新しい問題や授業事例を他の先生方が批評・参観し，その中で良いものはより広域に活用できるような環境や機会が整っています．
別の言い方をすると，「問題を作る人」「授業する人」「解く人（児童ら）」という分業体制ではない，ということです*8．これもまた，海外と比較したときの日本の特長と言っていいでしょう．それを象徴する本が"The Teaching Gap: Best Ideas from the World's Teachers for Improving Education in the Classroom"とその訳書『日本の算数・数学教育に学べ―米国が注目するjugyou kenkyuu』であり，当ブログではドイツは100，日本は50，米国は81，なぜ教材研究，教育も，支配から調和へといかないものかで取り上げています．
「かけ算の順序が反対だとバツにする事例」は，そういった経緯の中で普及し，遠山啓やWeb上の反論があっても，現在も授業に使われています．上のような国際的歴史的な背景があることを，ご理解いただければと思います．
（リリース：Sat Dec 22 06:39:15 JST 2012ごろ）
（最終更新：2012-12-26 朝）
*1:小学校でもそれらのパー書きの単位を陽には扱いませんが，単位量当たりの大きさや平均を求めることによって，分離量が連続量になり得ることには，注意をしたいところです．
*2:『Help Your Kids With Maths』では，わり算の解釈として「4 SWEETS ÷ 2 PEOPLE ＝ 2 SWEETS PER PERSON」，また計算の答えではいくつか単位付きの値も見られますが，かけ算の各因数には単位や助数詞に相当するものが書かれていません．
*3:電力量や仕事算を持ち出すのは，面積を避けるためです．面積は2つの因数が明らかに対等だけれども，電力量や多くの物理量などで，その2つの因数に役割は異なり，安易な交換は認められません．しかし，「2つの単位量から新たな単位量を得る」という共通点のため，面積に似た特性を持っています．
*4:用語だけでなく，内容面でも通読をお勧めします．「整数×小数」と「小数×整数」とで演算決定の正解率が違うという海外の報告（乗数効果）を日本で追試しているほか，かけられる数とかける数を交換して答えを出そうとした児童への配慮もなされています．
*5:このとき複数の式があり得るのは，問題集などを通じて確認できます．
*6:答案（式）から，児童の思考を正しく読み取れるのかどうかに疑問を持つ人なら，大人の書いた膨大な文書群の一部だけを見て，その人の思考を正しく読み取れる，なんて言いませんよね!
*7:「かけられる数とかける数を逆に書いたら間違い」とするのが学校教育，それに対して交換法則／トランプ配り／アレイを使えば正解になるよと主張するのが批判者，というねじれ現象も見られますが．
*8:Webで議論する人々---私を含め---は，「問題を作る人」や「授業する人」にケチをつけている人，でしょうか．
