- Park, J.-H. and Nunes, T. (2001). The development of the concept of multiplication. Cognitive Development, Vol.16, Issue 3, pp.763-773.
入手先や関連情報を:
- http://dx.doi.org/10.1016/S0885-2014(01)00058-2*1
- https://www.maa.org/external_archive/devlin/devlin_09_08.html*2
- wikipedia:en:Multiplication_and_repeated_addition
- http://togetter.com/li/480753
論文のアブストラクトの中に,"repeated addition"すなわち「累加」が6回,"correspondence"は「対応づけ」と訳してみましてこれが5回,出現します.
累加は,日本式なら3×5=3+3+3+3+3と思えばいいとして,対応づけという考え方は,かけ算の意味や指導において耳慣れません.これについては,本文中の図(p.768)が明瞭でした.

文字を書き出し,私訳を添えます.
Correspondence Group
The picture in the booklet was shown to the child. The experimenter said: 'Amy's Mum is making 2 pots of tomato soup. She wants to put 3 tomatoes in each pot of soup. How many tomatoes does she need?'
Repeated Addition Group
The picture in the booklet was shown to the child. The experimenter said: 'Tom has three toy cars. Ann has three dolls. How many toys do they have togather?'
(対応づけ群:ブックレットの図を子どもに見せる.実験者「エイミーのお母さんは,お鍋2杯分のトマトスープを作っています.お鍋1杯分のスープを作るのに,トマトを3つ使います.お母さんは,いくつのトマトを必要としますか?」
累加群:ブックレットの図を子どもに見せる.実験者「トムは,おもちゃの車を3つ,持っています.アンは,お人形を3体,持っています.2人のおもちゃを合わせると,いくつになりますか?」)
これらの事例を,小学校の先生方に見てもらい,日本はかけ算をどっちの方法で教えているかと尋ねれば,対応づけのほうを支持するはずです.トマトスープの問題は,学習指導要領解説に記されている,「乗法は,一つ分の大きさが決まっているときに,その幾つ分かに当たる大きさを求める場合に用いられる」に当てはまります.そして,おもちゃの問題のほうは,かけ算にしなくても,3+3で求めればいいのです.
「対応づけ」について,図ではなく文字で,その原理と例題が示されていました(pp.766-767).
In the correspondence group, the problems involved a fixed relation between two variables. This produces a structure with four values in the problem and the unknown could be different values in this structure. For example, Tom went to a sweet shop. He bought three sweets. One sweet costs three pence. How much money did he spend? The four values are one sweet, three pence, three sweets, nine pence (the unknown in this example).
(対応づけ群では,問題には2変量間で固定の関係が含まれている.その問題の中に4つの値があるような構造を生み出しており,未知の値は,その構造の中で異なる値となる.例えば,トムがお菓子屋さんに行き,お菓子を3つ買ったとする.1個3ペンスだと,いくら払ったか? この例で4つの値とは,「1個のお菓子」「(1個)3ペンス」「3つのお菓子」「9ペンス(未知の値)」である.)
このうち"a fixed relation"というのは,比例関係と見るべきでしょう.考察のところで,引用符つきで"proportions problems"という言葉も入っています.
それともう一つ,"four values"ですが,これよりさらに前で,1983年と1988年にVergnaudが書いたMultiplicative Structuresを引用(cite)しており,その影響と思われます.次の図です(次のステップ).

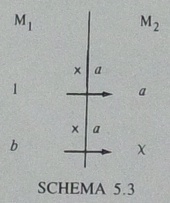
自分なりに「対応づけベースの乗法」を理解したところで,論文を読み直しました.イングランドのバッキンガムシャーにある2つの学校の2年生42名(男子23名,女子19名)をランダムに「累加群」「対応づけ群」に振り分け,それぞれの方法で指導します.たし算とかけ算の,事前テスト・事後テストを実施し*3,統計分析を通じて有意性を検証しています.たし算・ひき算は指導済みです.そしてかけ算・わり算は3年で学習することとなっているため,一方の学習のあとで他方を「施す」*4ことは考慮されていません.
事前・事後のテストでは,たし算・かけ算8問ずつを出題しています.論文では以下のとおり,それぞれの群で正解数の平均と標準偏差を求め,表にしています(p.770).

事前テストの時点で,累加群と対応づけ群の間に,ずいぶんと違いがあります.なので本文では,群間の比較というよりも,群内の比較すなわち「伸び」の統計分析に,字数をとっています.おそらくF検定を用いた,群間の比較も,その次のページに書かれており,結論としては"We conclude that practice in one-to-many correspondence as a means of solving multiplicative reasoning problems is significantly more effective than practice in repeated addition.",「かけ算の学習には,累加よりも対応づけ」といった次第です.
興味深い研究ではありましたが,このエビデンスでもって,小学校の算数のかけ算指導が変わったかというと,そうでもなさそうに思っています.もし変わったのなら,Keith Devlinの取り上げ方も,違っていたはずです.そして2つの指導手法の比較をするためのセッティングが作為的に見えます---両方を指導するだとか,指導外の手法・見方を活用するような子どもの行動だとかが,見当たりません.
そして"four values"の考え方にはいくつか欠陥があります.一つは,「1人ですると12分かかる単純作業,3人ですると?」といったタイプの問題でも,12×3としてしまう可能性です.もう一つは,答えの数量の把握が容易ではなく,実感を伴うことなく計算だけをする子になるという危惧です.それぞれ,4マス関係表の冒頭の出題,長方形の面積,数直線でかけ算わり算の後半と,関連します.とはいえこれらは,"four values"の考え方「のみ」で学習していく場合の課題であり,実際のところは,使える場面・使えない場面に注意して,活用していけばいいと思うのですけどね.
かけ算の問題を和訳しておきます(p.766).
Multiplicative reasoning problems
1. Ann's grandma went Christmas shopping. She bought seven boxes of presents for her grandchildren. Each box had two toys inside. How many toys did they have altogether?
2. We cannot see all the windows on the building because some windows are behind the trees. Can you tell me how many windows this buildings has altogether? (picture of building partially hidden by a tree; there are three rows of six windows in the front and the tree partially covers two rows)
3. There are four birdhouses in the woodland. Four birds live in each birdhouse. How many birds do they have altogether?
4. The row on top has four sweets. How many sweets do you think there are in the big row below? (picture shows a row on top with two sections and one below with six sections)
5. Five friends went to a fireworks show. Each child had to pay four pence to get a ticket. How much money did they spend altogether?
6. The blind on the window has star patterns (picture shows a blind with three rows of five stars). We cannot see all the stars because some are behind the fish tank. Can you tell me how many stars are there altogether?
7. Seven friends play a game with blocks. Each child has three blocks. How many blocks to they have altogether?
8. Two cupcakes cost eight pence. You buy four cupcakes. How much do you have to have to pay?
(かけ算で考える問題
1. アンのおばあさんはクリスマスの買い物に出かけました.そこで孫たちのために7箱のプレゼントを買いました.それぞれの箱には2つずつ,おもちゃが入っています.おもちゃは全部でいくつでしょうか?
2. ビルの窓が,木に隠れていて,すべてを見ることができません.全部でいくつの窓があるでしょうか?(図あり)
3. 森の中に,4つの巣箱があります.どの巣箱にも,4羽ずつ鳥が暮らしています.鳥は全部で何羽いますか?
4. 段の上には,4つのお菓子があります.大きな段の下には,お菓子がいくつあると思いますか?(図あり)
5. 5人の友達が花火を見に行きました.どの子どもも,きっぷを買うのに4ペンスを支払いました.お金は全部でいくら払いましたか?
6. 窓のブラインドには,星の模様があります(図あり).水槽の向こうにあるため,すべてを見ることはできません.星は全部でいくつあるか,言ってくれますか?
7. 7人の友達がブロックで遊んでいます.どの子どもも,3個ずつブロックを持っています.ブロックは全部でいくつありますか?
8. 2個のカップケーキが8ペンスします.4個のカップケーキを買います.いくら払うことになりますか?)