以下のとおり,はてブしてコメントをつけました.
takehikom かけ算の順序 "it is not clear why 4 cakes × 15 cents yields cents and not cakes" (Vergnaud, 1983)
http://b.hatena.ne.jp/takehikom/20131123#bookmark-170425294
この意図を書くことにします.大部分が過去に書いたものの切り貼りです.
まず「(Vergnaud, 1983)」の文献メモはhttp://www49.atwiki.jp/learnfromx/pages/46.htmlに挙げたとおりです.その文献で解説されている「乗法構造」について,今年1月,説明を試みています.
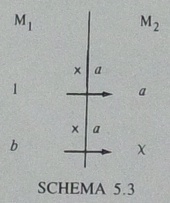
「量」と算数・数学教育の中で,もう一つ思い浮かぶのは,Vergnaudの文献です.「a×b=x」の構造を示す,2種類の図です(Vergnaud 1983, p.130).
次のステップ
その前のページには,"two measure-spaces M1 and M2"と書かれています.measure-spaceは「量空間」と訳すのがよく,中原2000, p.187においても,この語が使われています.
図の前後の本文を,直訳ではなく自分なりに解きほぐしていくことにします.以前にも少し書きましたが,今回はその詳細版です.
まず,「1個15セントのケーキを4個買います.いくらになりますか」という問題を考えます.aを15セント,bを4個とします.xは60セントであって,60個ではありませんね.SCHEMA 5.2, 同5.3とも,M1はケーキの個数の量空間,M2は金額の量空間です.
SCHEMA 5.2の考え方では,M1で1個から4個になるのを「×b」とします.同じ量空間における「b倍」を,M2へ適用することで,a=15セントの「4倍」がx=60セントになるわけです.
このとき,「×b」のbは,もはや「4個」ではありません.あえて量という言葉を使うなら,無次元量です.
SCHEMA 5.3は,横に見る関係といえます.1個だと15セント,という関係を「×a」で表します.そうすると,4個だと,「×15」とするので60セントです.
ちょっと注意したいのは,この場面での「×15」は,数だけ見れば15倍ですが,実際には,M1という量空間からM2という量空間へ変換しています.あるいは,「×a」が,M1とM2という2つの異なる量空間の仲立ちをしている,と考えることもできます.
このとき,「×a」のaは,これまた「15セント」ではなく,「15セント/個」とするほうが,より適切でしょう.言葉にすると,「1個(あたり)15セント」です.
量空間は,数学的に定義しているわけではなく,同じ性質の集まりという程度なのでしょう.その一方で,数学的な取り扱いでの「量」だと,連続量が対象とせざるを得ないところ,Vergnaudの議論では,ケーキの数や金額など,分離量も視野に入れています.
何に依拠するにしても,一長一短があるといったところで.
式に単位をつけることについても,いくつか書いてきています.
「子供が5人います。お菓子を2個ずつ配ると、お菓子は全部で何個になりますか?」という問題文に対して,児童が2×5=10と書いたとき,正解,すなわち場面を表した式であると判断するための考え方として,代表的と言えるものが3つあります.
まず最初は,「1あたり量×いくつ分=全体量」です.1あたり量は,パー書きの単位で表されます.今回の問題であれば,1人あたり2個ということで,「2個/人」です.いくつ分のほうは「5人」です.かけ算の式は「2個/人×5人」であり,計算をして「2個/人×5人=10個」を得ます.
(略)
2番目の考え方は,倍概念と呼ばれます.さらに分類ができるのですが,本日は簡単のため,「かけられる数と答え(積)の単位を同じにする」と「かける数の単位は,場面(問題文など)をもとにして付けるが,計算において無視される」という2個1組に限定します.これを理解するには,次の3つの文章題を見るといいでしょう.
- 子供が5人います.お菓子を2個ずつ配ると,お菓子は全部で何個になりますか?
- 袋が5つあります.お菓子を2個ずつ入れると,お菓子は全部で何個になりますか?
- 兄の持っているお菓子の数は弟の5倍です.弟は2個持っています.兄は何個持っていますか?
いずれも「2×5=10」です.かけられる数と積には「個」の単位がつけられますが,かける数は異なる単位です.ですがお菓子の個数の関係を見れば(図にすれば),いずれも同じです.これを共通化(一般化)させ,被乗数や乗数が小数・分数になっても適用できるようにした考え方が,倍概念というわけです.
「かけ算の順序」のダブスタ考
(略)
3番目は「一つ分の大きさ×いくつ分=全体の大きさ」…と言いたいのですが,これを含む大きな枠組があります.それは,場面を式で表すとき,式に単位は付けないという考え方です(1月5日 (1)(2)).
(略)
「子供が5人います。お菓子を2個ずつ配ると、お菓子は全部で何個になりますか?」という問題文に対して,児童が5×2=10と書いたとき,上の3つではそれぞれ,どのようにして正解・不正解を判断することになるのか,検討していきます
(略)
こうして場合分けをしていくと,「5×2=10を正解とするための理路」が見えてきます.「1あたり量×いくつ分=全体量」のみでは,不正解となり,これが「かけ算の順序は数教協も守っている」という主張の背景になります.そこに,遠山が著したトランプ配りか,『かけ算には順序があるのか』に記載されている法則・手法を加えることで,正当化できるわけです.
はてブ感謝リンク感謝(201311)
- 単位なし: 4×45=180
- 被乗数と積に単位: 4個×45=180個
- 被乗数はパー書き: 4個/人×45人=180個
- すべてに単位: 4個×45人=180個
そして,1960年代あたりまでは,「単位なし」と「被乗数と積に単位」が併存していました.1960年代から1970年代においては,そこに「被乗数はパー書き」が加わります.数学教育協議会(水道方式)の展開により,この式が普及する一方で,「被乗数と積に単位」の利用頻度が下がってきます.
式に単位(古いもの)
現在では,「単位なし」が算数の教科書や各種出題で採用されており,「被乗数はパー書き」は数教協のほか,その影響を受けた団体(学力研など)の指導に限られます.日常生活では,「すべてに単位」が,飲食物や日用品の数量表記でよく用いられています(略)
「1.5kg×4箱」に立ち返って,別のことを検討していきます.これ以外の表記はないのか,です.
1.5kg×4箱
まず思いつくのは,かける数とかけられる数の交換です.数だけを入れ替えて,「4kg×1.5箱」としてみます.「1箱は4kg入っていて,それが1.5箱分あったら,全部で何kgですか」という問題文を作ることはできます.しかし,算数の問題や手書きメモとしてならともかく,商品の数量表記として,「4kg×1.5箱」というのは不自然です.
これは,商品として「〜箱」は整数値であることが要請されるためです.量の用語を使うと,分離量です.
その一方で,かけられる数量については「1.5kg」でも「4kg」でも,問題となりません.それは連続量だからです.
連続量×分離量となるタイプのかけ算は,日常よく見かけることができます.算数でも取り扱いやすいため,Greer (1992)には「Equal measures」という名称がつけられています.日本ではというと,小数×整数を4年で,分数×整数を5年で学習し,小数のかけ算(整数または小数×小数)や分数のかけ算(整数または分数×分数)よりも1学年,先に学習しています.
あともう一つ,「1.5kg×4箱」から,×の左右をそっくり入れ替えて,「4箱×1.5kg」とすると,自然でしょうか,不自然でしょうか.
上に書いた《楽観的解法》により,総量は6kgであって6箱ではないというのは,想像できます.
ですが現実として,「4箱×1.5kg」は,まず見かけません.これは「かけ算したら(《倍》で解釈したら)6箱になるから」ではなさそうです.
もっとも有望な理由づけは,「1.5kg×4箱」だと「1.5kgが4箱」と素直に読めるのに対し,「4箱×1.5kg」について,そうはいかないことです.「4箱が1.5kg」では,数量・個数の関係が不明ですし,「4箱で1.5kg」と言ったら,4箱合わせて(6kgではなく)1.5kgであるように聞こえます.「4箱あって,それぞれ(の箱は)1.5kg」と言うと,今度は長くなります.
見直してみると,《パー書き》のところで書いた,「1箱あたり1.5kg,それが4箱」も長いのです.算術や算数,その中でも《倍》を根拠としながら,簡潔に書けて誤解も少ない,実用性に優れた数量表記が,「1.5kg×4箱」です.
交換については,そんなところですが,別のアプローチとして,字数の削減を見ておきます.もし,「1.5kg 4箱」と書いたら,どうなるでしょうか.
これはやはり,「1.5kgが4箱(総量は6kg)」なのか「4箱で(総量は)1.5kg」なのかが曖昧です.
ここに「×」の意義があります.《倍》を知っていれば,「×」の左側が,1まとまりの数量となるのが明確なのです.
次に,「1.5kg×4」では,いけないのでしょうか.
いけないわけではありません.海外の商品では,3×80gや75g×5を確認しています.そのほか,コカコーラ商品のペットボトルの箱詰めは,2L×6と,《倍》なのをこれまで見てきています.
そこについては,簡潔さと親切さの兼ね合いだと思っています.現状は「1.5kg×4箱」「2L×6」といった書き方が広く採用されています.「3×80g」は海外の製品であり,そして,「1.5kg/箱×4箱」や「4箱×1.5kg」に相当するような物品の数量表記は,目にすることができないのです.
- A-5: 単位を付けて書くと,「5×3個」と「3個×5」,「5枚×3個/枚」と「3個/枚×5枚」は,それぞれ同じである.
(略)
A-5に書いた「単位」について,Wikipedia日本版では「助数詞」[Link 4J]で詳しく解説されている.英語版には"Japanese counter word" [Link 5E]がある.また単位付きの式は,算数の教科書には見当たらない.しかしこれは日本固有というわけではなく,[Schwartz 1988]に記されている"referent"が相当しており,国外の数学教育の研究にも事例が見られる.さらに言うと,「/ (per)」を用いた分離量の単位表記は1970年ごろ発生したものである(「/」を積極的に推進している数学教育協議会の著作物で,1961年と1971年に発行された『水道方式入門』[遠山1961][遠山1971]を読み比べるとよい).
(略)
- B-5: 単位を付けて書くと,「5個×3」と「3個×5」,「5個/枚×3枚」と「3個/枚×5枚」は,それぞれ異なる.
(略)
かけ算の順序論争について(日本語版)
純粋な数のかけ算と,算数で答えを求めることとの違いは,VergnaudやGreerも指摘している.Vergnaudの指摘とは,すでに述べた「4×15と15×4は等しいけれども,4個×15セントによって60セントが得られ60個ではないのはなぜか」であり,これは乗法構造を詳述する直前に記されている.Greer [Greer 1992]は,「あるロケットは1秒間に0.85マイルのスピードで進む.16秒ではどれだけ進むか?」なら,子どもたちはかけ算を選ぶが,0.85と16を交換した文章題になると16÷0.85を選びやすいと例示し,実験により認められた「乗数効果」を解説している.ここで乗数効果とは,かけ算で求められると認識・選択することの困難さが,かける数が「整数」「1より大きい小数」「1より小さい小数」のうちどれであるかに依存し,かけられる数の種類には依存しないことをいう.乗数効果は国内でも確かめられている[小原2007].
「かけ算の順序」の批判者は,しばしば「かけられる数×かける数」は導入時の便法であり,交換法則を学習すれば「かける数×かけられる数」としてもよいと説く(例えば[高橋2011]).しかしそれでは,上に挙げたVergnaudやGreerの提案や観察を合理的に説明できない.
Q: 「5まい×3こ/まい=15こ」のように,式に単位を書かせたらいいのでは?
「×」から学んだこと 13.04―かけ算の意味・式の意味
A: 「式は世界共通」という考え方との,勝負になるでしょうね.現状として,小学校の算数では,その種の式は採用されていません.
算数・数学(という科目)で,式に単位を付けないのは,結局のところ「決まり」です.(かさ(dLなど)や角度の計算で,「dL」「°」を添えている式を,問題集で見ることもできます.学習指導要領解説には,「1m^2=10000cm^2」の等式が入っています.)
式に単位を組み込むのは,組立単位や次元解析と合わせて,高校の物理・化学あたりで理解し活用するのがいいように思います.
昨年,「親として,我が子はこうあってほしいと願う権利がある一方で,学校や親の要求に対して自分なりに調整し,その都度「答えを出していく」のは子ども自身である」と書きました.そう思うようになった一節を,抜き出します.
『いろいろな量 (子どもを賢くする?よくわかる算数の授業 )』面積図は門前払いもう40年以上も前のことですが,筆者は子どもの算数の教科書を見ると単位をつけていないので,これでは数学ができなくなってしまうと思い,自宅で教えるときは式には単位をつけることを要求しました。上の男の子は私が相手のときは単位をつけ,学校ではつけないと使い分けました。結局両方でマルを貰っていたわけです(これはあとで知ったことです)。一方,下の女の子は頑固に学校の先生の方針に従い,私のいうことは聞こうとはしませんでした。案の定,上の男の子の方が数学の実力はつくようになりました。
その結果はどうなったかというと,ともに東京大学に入学できましたが,男の子は理学部数学科に進学したのに対して,女の子は教養学部教養学科でした(もっともこの女の子も今は高校の数学教師をしていますが)。
(p.7)
今月出た本には,次のとおり書かれています.
①1はこに4こずつケーキが入ったはこが、5はこあります。
ケーキはぜんぶで何こになるでしょう。「1はこに4こずつ」なので、1あたりの数は、4こです。そのはこが5はこあるので、入れものの数は、5はこです。ぜんぶの数をもとめたいので、4こ×5はこの、かけ算になります。(略)
(式) 4こ×5はこ=20こ
(答) 20こ
このとき、5はこ×4こ=20こ とするのはまちがいです。かけ算の式は、かならず、1あたりの数×入れものの数(いくつ分)=ぜんぶの数とします。
(『陰山メソッド「徹底反復 算数プリント」小学校1~6年 (コミュニケーションMOOK)』p.102)
出版年月日について,Amazonでは「2013/10/29」と出ますが,手元の本は「2013年11月3日初版第1刷発行」となっています.記述の中で,パー書きでないのに「1あたりの数」と表現していることには,違和感を覚えますが*1,ここでは,最新の,しかも「陰山メソッド」で有名な教育者の著書にも,いわゆる「かけ算の順序」や「単位をつけたかけ算の式」への見解が書かれている点を,ご留意いただければと思います.
「掛け算の順序」に批判的な人々は,自分の考えを書籍や論文と照合しようとしない,という個人的な観察結果をもって,本記事を締めくくることにします.
さっそくのコメント,ありがとうございます.
NOV1975 ここまで理屈を付けないと説明できないことを当然子供が自然に理解できることはないと思うんだけどなあ。最終的に答えになんの単位をつけるかが重要でしかないように思える。
私には,複数のはてブコメントで提案・支持されている「2耳/匹×3匹」などのほうが「理屈付け」に見えます.そして算数教育の歴史からすると,2耳/匹に代表される“1あたり分離量”は,新しい表記法なのです.
それと「最終的に答えになんの単位をつけるか」よりもむしろ,場面がどのような数量的な関係(加法か,減法か,乗法か,除法か,その組み合わせか)になっているか,子どもたちが認識できるようになることを,教科書や授業では重視していると理解しています.それは,2008年改訂の学習指導要領で,数量関係の領域が第1学年から設定され(それまでは第3学年以上),2年でも「乗法の式」について事項と説明が入っていることが,大きく関わっています.
ところで,これはnovtanさんではなく元の人の責任ですが,ウサギの耳はかけ算の教具として「古い」です.「6×4,4×6論争にひそむ意味」でウサギの耳を使って記事を書いた遠山は,死去する半年前の講演で,釈明とともに「シェーマとしてはあまりうまくない」と述べています(http://d.hatena.ne.jp/takehikom/20121215/1355501672).
lastline やっぱりよく分からないという、すんなり入らない。教育の歴史的にと言われても、掛け算の順序が話題になるのは間違った子がいて理解てできてないからで、教育効果は十分にあるの?という疑問が
私は小学校の教育に携わっていない者なので,外野からの意見ですが*2,学校のテストにせよ,より広範囲な学力調査にせよ,どの子も(学習指導要領などの公的文書や,担任の先生が設定したねらいに基づく)学習事項を正しく理解することは,「戦争のない世界」と同じくらい,理想を追い求めているもので,現実にはできっこないと思っています.そこで,いわば次善の策として,どのくらい理解されているのかを質的・量的にとりまとめたり,間違えた子には回復学習を施したり,間違いの傾向を分析して次年度以降の授業に役立てたりだとかいったことがなされています.
この認識が間違っていないのなら,「間違った子がいて」については,「その子(たち)にアドバイスしましょう」になると思います.アドバイスをするのは,学校の先生ばかりではなく,教育を受けさせる義務を負う者(多くは子どもの親)や,周囲の者も,可能です.「教科書を開けてごらん.ここに書かれてるでしょ」と行くか,「世の中では掛け算に順序がないんだよ,だからこんな問題でバツにされたからって気にするな」と行くかは,ケースバイケース,あるいは人それぞれであり,この対処法の違いが,「よく分からない」「すんなり入らない」の表明につながっていると,考えています.
なお,この論争に関して,大きなレベルでの個人的認識には「ある出題と,バツがつけられている状況から,そこで教師の期待する『かけ算の構造』を指摘し,数学は,あるいは世の中は,そうではないよ(それだけではないよ)と主張している」(かけ算の問題の構造改)を持っています.
(最終更新:2013-11-24 朝.『陰山メソッド 徹底反復 算数プリント』について,Amazonへの直リンクをつけました.)
*1:もう一つ,リットルなどが斜体になっているのも,気にかかりました.関連:http://www.tokyo-shoseki.co.jp/e-mail/qanda/q-es-math.htm#q15
*2:プログラミングなどの授業を担当している,1人の大学の教員の意見としては,診断的評価・形成的評価・総括的評価に代表される(やや古いけれども)教育評価の考え方は,授業の計画や長期的な改善に大いに役に立っています.ティーチングアシスタントをしていた学生から「自分が受けたときよりも分かりやすい内容になっていますね」と言われたときに,そのことを実感します.