いきなりですが問題です.
求める式と答えを書きましょう.
(1) 1時間は,60分です.2時間は,何分ですか.
(2) 240分は,何時間ですか.
さっそくですが解答です.(1)は,1時間=60分が2つということで,60×2=120 答え120分です.(2)は,240÷60=4 答え4時間です.
さらにですが問題です.
(3) 48分は,何時間ですか.
(4) 0.4時間は,何分ですか.
分を60でわれば,時間になるのですから,(3)は,48÷60=0.8 答え0.8時間となります.
時間を分にするのは,その逆演算とみて,60をかけるとしましょう.そうすると,(4)は,0.4×60=24 答え24分です.
こうして並べたときに,(2)と(3)はともに「60でわる」によって答えを求めていますが,(1)では60がかけられる数,(4)ではかける数となっています.
このような式の多様さは,Vergnaud (1983, 1988)の知見をもとにすると,理解しやすくなります.(1)の式は,1時間(60分)の2倍です.たし算(累加)で60+60=120と求めることもでき,これもまた,60×2の根拠となります.
それに対し,(4)のかけ算の式「0.4×60=24」では,「時間」の量空間をイメージすることからはじめます.「何時間」で表される数量すべてからなる集合です.次に,「分」の量空間も,同様にイメージします.
それらの量空間の仲立ちとなるのが,「時間の値を60倍すれば,同じ(時間的な)長さの,分の値になる」という性質であり,略すと「時間に60をかければ,分になる」です.その逆演算は,「分の値を60分の1にすれば,同じ(時間的な)長さの,時間の値になる」であり,「分を60でわれば,時間になる」です.
ここで60倍というのは,1時間=60分,2時間=120分,0.8時間=48分など,同じ(時間的な)長さになる2つの数量を対応づけるものとなります.異種の2つの量の対応づけは,小学校では4〜6年で学習します(ただし単元名に「単位の換算」というのは見当たらず,代わりに「変わり方」「比例」などになります).
「空間をイメージ」を,小学校の算数で実現するには,対応表です.

かけ算・わり算の関係をつけると,以下のように表せます.
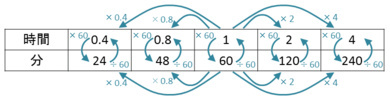
大人の世界では,ここまでの内容をもとに,(1)に2×60の式を立てて,答えが求められると言ってもいいのですが,Vergnaud (1988)で取り上げられている,おもちゃの車の問題をふまえると,2×60は,低学年の子どもたちにはなじみにくいかもしれません.おもちゃの車の問題*1に関して,書かれていたのは,"Twenty dollars cannot be 5 cars + 5 cars + 5 cars + 5 cars."です.今回の話なら,"120 minutes cannot be 2 hours + 2 hours + ... + 2 hours."となります.
ここでさらに,問題です.
「0.4時間は,何分ですか.」をかけ算で求めるとき,何がかけられる数,何がかける数であるべきでしょうか.
優等生的な解答はというと,60×0.4でも0.4×60でも求められるので,「どちらでもいい」なのですが,ここに,出典を挙げて一つの答えを導出せよ,という条件をつけ加えるなら,60をかけられる数,0.4をかける数にするのが良さそうです.
参照するのはGreer (1992)です.乗除算のモデル表の"Measure conversion"に着目します.そして表の,他の内容と合うようにするなら,60をかけられる数*2,0.4をかける数に対応づけるのが自然です.
「0.4時間は,何分ですか.」をもとにすると,乗除算の問題文は,次のように書くことができます.
- Multiplication problem:1時間は,60分です.0.4時間は,何分ですか.
- Division (by multiplier):0.4時間は,24分です.1時間は,何分ですか.
- Division (by multiplicand):1時間は,60分です.24分は,何時間ですか.
Greerの表にはかけ算・わり算の式はこうだと明記されていませんが,上の2番目の文章題から,24÷0.4=60と書くことができ,0.4が,multiplier(かける数)です.また3番目の文章題は,24÷60=0.24という式になり,60が,multiplicand(かけられる数)です.
ここから,Greerの文献を離れた考察をします.3つの文章題を書きましたが,2番目の「0.4時間は,24分です.1時間は,何分ですか.」には違和感があります.「1時間は何分かなんて,60分だよ,『0.4時間は,24分です』は,いらないよ」と,ツッコミができるのです.
算数でそんな問題を出すわけにいかないからと,取り除いたら,「0.4時間は,何分ですか.」のタイプと「24分は,何時間ですか.」のタイプが,時間・分の相互換算の問題として考えられます.実質的に,1つのかけ算に1つのわり算という関係になります.
このことは,「分を60で割ると時間」「時間に60をかけると分」---「60に時間をかけると分」ではなく---というルールに至る理由となるようにも思います.
以下は書誌情報と,当ブログでの紹介記事です.
- Vergnaud, G. (1983). Multiplicative Structures, In Lesh, R. and Landau, M. (Eds.), Acquisition of mathematics concepts and processes, Academic Press, pp.127-174. isbn:012444220X
- Vergnaud, G. (1988). Multiplicative Structures. In Hiebert, J. and Behr, M. (Eds.), Number Concepts and Operations in the Middle Grades, Vol.2, pp.141-161. isbn:0873532651
- Greer, B. (1992). Multiplication and Division as Models of Situations. In Grouws, D. A. (Ed.), Handbook of Research on Mathematics Teaching and Learning, National Council of Teachers of Mathematics, pp.276-295. isbn:1593115989
- かけ算と構造
- かけ算・わり算でモデル化される場面
- 海外では,「かけ算の順序」「たし算の順序」についてどのような見解を出していますか?
本日の記事を書こうと思ったきっかけは:
乗法ではかえって同一単位の量どうしの積の意味が薄いようです.縦の長さ×横の長さ=長方形の面積 といった公式も,縦の長さ(側長)と横の長さ(幅)を別種の量と見て,その積によって面積(という新しい量)を定義する,とでも考えたほうが理解しやすいかもしれません.単位の換算も,Aの単位=BのC単位*3 という換算率が明確なら,A,Bそれぞれで測った量a,bに対し,a=b×cという公式で換算できます.第3章で述べる分数も「単位の換算」という一面があります.教育上ではこの種の自由な発想・解釈を許容すべきです.
(『数の世界 (サイエンス・パレット)』p.41)
それと,http://togetter.com/li/742591のコメントにも「単位の換算」のやりとりがあります(takehikomの名前でコメントしています).