「3口のたし算」とは,a+b+cで表される式や場面です.小学校では1年で学習します.aとbとcは,同種の数となります.量に拡張して,0.1L+0.1L+0.1L=0.3Lと計算することもできます*1.
本記事で焦点を当てたいのは,「3口のかけ算」です.a×b×cで表されます.3年で,結合法則の学習で見かけるのですが,3口のたし算とちがって,aとbとcがそれぞれ,異種の数・量になりやすいことに気づきました.
結合法則の理解や学習に限定することなく,a×b×cで表される例を,《倍の合成》《箱売り》《2つに比例》《3番目まで》《直方体の体積》と命名し,その具体例や,どんなかけ算をしていいか,してはいけないかに注意しながら,ちがいを見ていくことにします.
次元を含む式の表記
本題に進む前に,表記についておことわりです.
小学校の算数では,式に単位を付けません.「a×b×c」と書いたとき,aもbもcも,純粋な数であり,0以上の有理数(整数・小数を含む)です.
ですが,具体的な場面をもとに,式で表したり,a×bといった式の意味を読み取りやすくするため,数と量との対応づけを,ルールとして設けておきます.
具体的には,3つの数a,b,cに対応する量を,それぞれn1[d1],n2[d2],n3[d3]と表記します.nはnumber,dはdimension(次元)の頭文字です.
次元にあたるのは,m(メートル)などの普遍単位だけでなく,パー(/)や中点(・)を含む組立単位となることもあります.「個」などの分離量の単位も,次元に使用できるものとします.
また無次元量のときは,[…]を取り除いてn1,n2,n3と書きます.
2口のかけ算…とは言いませんね,2つの因数をとる,1回のかけ算には,以下の4つの類型があります.
- 倍:n1[d1]×n2=n1n2[d1]
- 比例:n1[d1/d2]×n2[d2]=n1n2[d1]
- 量の積:n1[d1]×n2[d2]=n1n2[d1・d2]
- 直積*2:n1[d1]×n2[d1]=n1n2[d1]*3
《倍の合成》《箱売り》《2つに比例》《3番目まで》《直方体の体積》は,この4種類の類型を複数(同一の類型を複数というのもあります)用いて,構成や解釈をすることができます.
abcはアルファベット順なのに,次元付きの量では通し番号を用いている点はなにとぞご容赦ください.
《倍の合成》
啓林館の教科書には次のような問題があります.
雲梯と木と校舎の高さを比べました。
雲梯の高さは2mです。
木の高さは,雲梯の高さの3倍です。
校舎の高さは,木の高さの2倍です。
校舎の高さは,何mですか。
校舎の高さは,式 2×3×2=12,答え 12mと求めることができます.最初の因数2は雲梯の高さで,「×3」と「×2」が,問題文にあるとおり3倍と2倍を表します.
この例を一般化すると,ある量n1[d1]をn2倍し,さらにn3倍すると,どれだけの量になるかを求めるので,n1[d1]×n2×n3=n1n2n3[d1] となります.
この式は,n1[d1]×n2×n3=(n1[d1]×n2)×n3=n1n2[d1]×n3=n1n2n3[d1] という式変形と,n1[d1]×n2×n3=n1[d1]×(n2×n3)=n1[d1]×n2n3=n1n2n3[d1] という式変形を含んでいます*4.それぞれの2番目の式から,(n1[d1]×n2)×n3=n1[d1]×(n2×n3)あるいは(a×b)×c=a×(b×c)すなわち乗法の結合法則を確認することができます.
このケースでは,n1[d1]×n3という,「×n2」を取り除いたかけ算の意味を説明するのが困難です.上述の雲梯と木と校舎の場面で,2×2=4で得られる4mは,3つの高さのいずれを表したものにもなりません.
《箱売り》
Webで読めるものから.第3学年 算数科学習指導案(平成18年10月24日,調布市立杉森小学校)にある,「今日の問題」です.
1こ90円のシュークリームが、1はこに3こずつ入っています。
2はこ買うと、代金は何円になるでしょう?
シュークリームの数を求めてから,全部の代金を求めると,3×2=6,90×6=540で,まとめて90×(3×2)=540と表します.1箱の代金を求めてから,全部の代金を求めることにすれば,90×3=270,270×2=540となり,これは(90×3)×2=540です.
そうして授業では90×(3×2)=(90×3)×2を導き,「かけ算はかける順番がかわっても、答えは変わらない」とまとめています.
2つの求め方の式に,次元を添えて表すと,次のようになります.先にシュークリームの数を求める場合は,3[こ/はこ]×2[はこ]=6[こ],90[円/こ]×6[こ]=540[円] です.
先に1箱の代金を求める場合は,90[円/こ]×3[こ/はこ]=270[円/はこ],270[円/はこ]×2[はこ]=540[円] です.このとき,パー書きの量どうし,言い換えると内包量どうしのかけ算(Schwarzが示した,I×I'=I'')が発生します.
この事例は,n1[d1/d2]×n2[d2/d3]×n3[d3]=n1n2n3[d1] と表すことができます.
この関係式では,《倍の合成》と同じく,2番目の因数を抜かしたかけ算に,意味を与えることができません.実際,n1[d1/d2]×n3[d3]=n1n3[d1・d3/d2] としたところで,この右辺が何を表すのか,説明が困難です(それに対し,n1[d1/d2]×n2[d2/d3]=n1n2[d1/d3] と n2[d2/d3]×n3[d3]=n2n3[d3] は,シュークリームの個数・値段に基づいて説明ができます).もとの学習指導案では,自力解決の段階で,「90×2=180 180×3=540」という式を,予想される児童の反応として載せています.しかし「机間指導する」とも書かれており,この授業では間違いとみなしています.
《倍の合成》との相違点も見ておきます.《倍の合成》では,後ろ2つの「〜倍」を合成して新たな「〜倍」を得ましたが,この《箱売り》は,前2つの内包量を合成して,新たな内包量をつくります*5.「新たな内包量」なのは,n1[d1/d2]×n2[d2/d3]=n1n2[d1/d3]に出てくる3つの次元がちがっていることから確認できます.
《2つに比例》
これは独自に考案した問題です.
5人家族があります.それぞれ,1日に3個ずつ,ミニトマトを食べます.7日間で,この家族は全部で何個のミニトマトを食べるでしょうか? 式と答えを書いてください.
解答は難しくありません.5人家族で1日に3個ずつ,ミニトマトを食べるというので,この家族が1日に食べるミニトマトは3×5=15で15個です.7日間ですから,15×7=105 答え105個となります.
また別の考え方もできます.1日に3個ずつ,7日間ですから,1人が食べるミニトマトは3×7=21で21個です.5人いますので,21×5=35 答え105個となります.
どちらの方法でも,105個を得るようにするには,ミニトマトの「3個」の量の表現に少し工夫をします.具体的には,「1人が1日に3個」のミニトマトを食べると解釈して,3[個/人・日] という量で表します.
そうすれば,家族で1日に食べる個数に着目するなら,3[個/人・日]×5[人]×7[日]=15[個/日]×7[日]=105[個] を得ますし,7日間で1人が食べる個数に着目するなら,3[個/人・日]×7[日]×5[人]=21[個/人]×5[人]=105[個] を得ることができます.
一般化すると,n1[d1/d2・d3]×n2[d2]×n3[d3]=n1n2n3[d1] となります.
この式には2つの交換可能な箇所があります.「×n2[d2]」と「×n3[d3]」,それと,最初の因数の単位にある「d2・d3」です(n1[d1/d2・d3]=n1[d1/d3・d2]).1番目と3番目の因数の積は意味のある量,という点で,《倍の合成》や,《箱売り》とは異なる関係となっています.
2番目と3番目の因数の積を求めると,どうなるでしょうか.形式的には,n2[d2]×n3[d3]=n2n3[d2・d3] であり,総数の計算式は,n1[d1/d2・d3]×n2[d2]×n3[d3]=n1[d1/d2・d3]×n2n3[d2・d3]=n1n2n3[d1] となります.ミニトマトの問題で考えると,[d2・d3]は「人日」を指します.3個をミニトマトの「1食」と見なし,[人・日]と[食]を同一視すれば,3[個/食]×5[人]×7[日]=3[個/食]×35[食]=105[個] と計算ができます.
「独自」と書きましたが,先例はあります.Vergnaudが,スカウトキャンプでのシリアルの消費量として例示しています.「複比例」と密接な関係のある内容でした.
《3番目まで》
学校図書の6年の算数の教科書には,「ならび方が何通りあるかを,計算で求める」という,発展的内容の出題があります.「Aさん,Bさん,Cさん,Dさんの4人の子どもがいます。4人がならぶと何通りのならび方があるか考えましょう。」という問題です.教科書のヒントにも注意すると,そこで式として,期待されるのは,「4×3×2×1」です.これでは4口のかけ算ですね.
3口のかけ算になるよう,問題をつくってみます.
Aさん,Bさん,Cさん,Dさんの4人の子どもが競走します.
1位,2位,3位の組み合わせは何通りあるか考えましょう.
1位は4人のうちの1人なので,4通りあります.2位は,1位の人を除いて,3通りあります.3位は,1位と2位の人を除いて,2通りあります.ということは,1位から3位までの組み合わせは,4×3×2通りとなります.
ここで少し,「かけ算の順序」について書いておくと,4人が競走して1位と2位の組み合わせは,上と同様の考え方から,4×3で12通りと求めることができますし,Aさんが1位のときの組み合わせは3通り,他の人も同様ということで,3+3+3+3通りを累加と見なして3×4で12通りとすることもできます.3位までを求める式も,同様に2×3×4です.これはボトムアップのアプローチと関わりがあります.それに対し,「1位は…,2位は…,3位は…」とそれぞれ何通りかを押さえてから,順にかけるのは,トップダウンのアプローチです.
この「順列・組み合わせ」のかけ算は,3つの因数に制約があります.トップダウンの場合,1ずつ小さくなります.また上位から,何通りあるかを考える必要もあります.1位の人を決めていない状態で,「2位は3通り」と言えませんし,1位と3位を先に決めた(4人のうちそれぞれ誰なのかが分かっている)ときも,「2位は3通り」と言うわけにいきません.
次元を用いた式ですが,前述の直積に基づいて,n1[通り]×(n1−1)[通り]×(n1−2)[通り]=n1(n1−1)(n1−2)[通り] と表せます.[通り]×[通り]=[通り]が不自然だというなら,「〜通り」は「〜倍」と同じく,無次元量と考えることにすれば,n1×(n1−1)×(n1−2)=n1(n1−1)(n1−2)を得ます.
《直方体の体積》
さっそくですが問題です.
幅が3m,奥行きが4m,高さが2mの直方体の体積を求めましょう.
式は3×4×2=24,答えは24㎥です.
これは,3つの因数をどの順序にしてもいいでしょう.本から,図を(『Teaching Mathematics in Grades K-8: Research Based Methods』p.179).
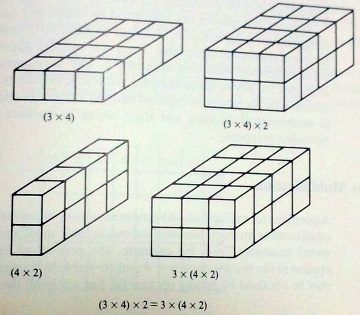
次元を含んだ式は,n1[d1]×n2[d1]×n3[d1]=n1n2n3[d1^3] となります(「^3」は上付きの3).途中の式まで書くのなら,n1[d1]×n2[d1]×n3[d1]=(n1[d1]×n2[d1])×n3[d1]=n1n2[d1^2]×n3[d1]=n1n2n3[d1^3] がその一例です.どの順序で計算しても,長さ(1次元),面積(2次元),体積(3次元)の順に量を知ることになります.
ただし,上の図を,単位立方体の総数を求めるとしたら,次元が変わってきます.具体的には n1[個]×n2[個]×n3[個]=n1n2n3[個] です.すべての次元が同じ「個」なのは,直積を適用したからです.
パー書きを使うなら,n1[個/列]×n2[列/段]×n3[段]=n1n2n3[個] でしょうか.これは,《箱売り》と同じ,2つのパー書きの式です.この式でも,n1[個/列]×n3[段]を求めるとおかしなことになりますが,単位立方体を3次元に配置して直方体を構成しており,幅・奥行き・高さは任意に選べますから,n1[個/列]×n3[列/段]×n2[段]=n1n2n3[個] とすることができます(n1[個/列]×n3[列/段]=n1n3[個/段] も,n3[列/段]×n2[段]=n3n2[列] も,図のどれに当たるか,説明ができます).《箱売り》との類似点・相違点を見ることができました.
まとめ
- 《倍の合成》
- a×b×c=n1[d1]×n2×n3=n1n2n3[d1]
- (a×b)×cとa×(b×c)とで,途中で求める量の種類が異なります.
- a×cの意味を説明するのが困難です.
- 《箱売り》
- a×b×c=n1[d1/d2]×n2[d2/d3]×n3[d3]=n1n2n3[d1]
- (a×b)×cとa×(b×c)とで,途中で求める量の種類が異なります.
- a×cの意味を説明するのが困難です.
- 《2つに比例》
- a×b×c=n1[d1/d2・d3]×n2[d2]×n3[d3]=n1n2n3[d1]
- bとcは交換可能であり,(a×c)×bとしても,同じ量を得ます.
- (a×b)×cとa×(b×c)とで,途中で求める量の種類が異なります.
- 《3番目まで》
- a×b×c=n1[通り]×(n1−1)[通り]×(n1−2)[通り]=n1(n1−1)(n1−2)[通り]
- c×b×aと逆順で表すことが可能です.
- a×cの意味を説明するのが困難です.
- 《直方体の体積》
- a×b×c=n1[d1]×n2[d1]×n3[d1]=n1n2n3[d1^3]…連続量
- a×b×c=n1[個]×n2[個]×n3[個]=n1n2n3[個]…分離量
- a,b,cはいずれも交換可能であり,(a×c)×bとしても,同じ量を得ます.
*1:Lはリットルです.この単位記号を文字と見れば,形式的処理をするのに都合がよさそうですが,0.5L+0.5L=Lではなく1Lなのは要注意です.
*2:「場合の数の積の法則」でもあります.
*3:次元[d1]は,「通り」「個」が典型的です.またアレイを直積に基づいて解釈すると,長方形に並べた机の台数を,4[台]×6[台]=24[台] と表すこともできます.
*4:前者は「量×数」を2回,行っているのに対し,後者は「数×数」をしたあと「量×数」を行います.
*5:「かける数が内包量」を3口のかけ算に拡張して,n3[d3]×n2[d2/d3]×n1[d1/d2]=n1n2n3[d1] とするのは,どうでしょうか? …いえ,不自然です.シュークリームの例に適用すると,「2はこ」が,最初に提示される量となります.買うときにシュークリームの箱の数から着目する人はまずいませんし,シュークリームをもらう立場だとしても,まず箱数,次に箱あたりの個数,最後に単価の順で,情報を知るのが,はたして自然でしょうか?)