いきなりですが問題です.
円の中心と円のまわりの2つの点を結んでできる三角形は,どんな三角形でしょう。
さっそくですが解答です.二等辺三角形ですね.頭の中で描けますが,あとで図を示します.
元ネタは以下のとおりです.
- 前田一誠: 教師のちょっとした言動によって…, 算数授業研究, Vol.102, 東洋館出版社, pp.8-9 (2016). isbn:9784491031798
著者が参観したという,3年の授業の出来事です.三角形,二等辺三角形,正三角形は学習済みです.
板書された上記の課題に対し,児童らがめいめいのノートに,コンパスで円を描き,円周上で自由に2点をとって,円の中心と合わせて3点を結ぶよう,展開していきます.
そんな中,ある男の子が「できない」と言いました.著者はその状況を,アクティブ・ラーニングのチャンスととらえ,肯定的に論評しています*1.
結んで三角形ができた状況と,できない状況は,それぞれ以下のとおりです(p.8をもとにtakehikomが作成).
できた: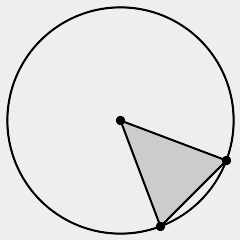
できない: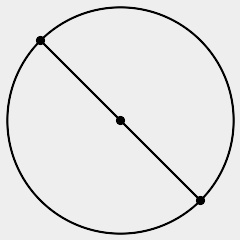
言葉にすると,こうです.3つの点が同一直線上にあるとき,あるいは(同義ですが)円のまわりの2つの点を結んだら,その円の直径となるとき,三角形をつくることができません.
この指摘は確かにその通りと理解した上で,では,この事実が,もとの問題に影響するでしょうか.「できない場合もある」を,答えに加えるべきでしょうか.
そうではなさそうです.というのも数学の読み方として,「円の中心と円のまわりの2つの点を結んでできる三角形」と書かれてあれば,「円の中心と円のまわりの2つの点を結んで三角形にならない」場合は対象外となることを,そこに含んでいるからです.
問題文を「円の中心と円のまわりの2つの点を結んでできる図形は,どんな図形でしょう。」にすれば,話が変わってきます*2.これは,「xの一次方程式ax=bを解け(a,bは定数とする)」とすると,a≠0が暗黙のうちに仮定されているけれども,「一次」を取り除いたら,a=0の場合も考えないといけないのと,類似しています.
とはいえ,p.8の図の直前の段落を読むと,著者が参観したという,授業においても,同一直線上にある場合は対象外となる指導がなされていたと判断できます.(おそらく)その場の先生も(おそらく)子どもも,(おそらく)取り上げた著者も,そして(確実に)読んだ自分も,これは面白いと思うことのできた授業でした.
作図コマンドは以下のとおりです.A2で使用したものを改変しました.実行には,ImageMagickのconvertコマンドが必要です.
convert -size 240x240 'xc:#eee' -draw "translate 120,120 fill none stroke-width 2 stroke black circle 0 0 80 80 fill #ccc polygon 0 0 40 106 106 40 fill black stroke none circle 0 0 3 3 circle 40 106 43 109 circle 106 40 109 43" -quality 95 circle1.jpg
convert -size 240x240 'xc:#eee' -draw "translate 120,120 fill none stroke-width 2 stroke black circle 0 0 80 80 line -80 -80 80 80 fill black stroke none circle 0 0 3 3 circle -80 -80 -83 -83 circle 80 80 83 83" -quality 95 circle2.jpg
*1:それに続く,p.9の「しなければならない」を含む話は,共感できませんでした.「かけ算の順序」論争に対する自分のバイアスが,関わっているのだと思いつつ.
*2:三角形にならない場合は,直径のほかに半径も考えられます.すなわち,円のまわりの1点を「2つとる」ことにして,中心と結ぶのです.とはいえこれは,除外していいでしょう.ところで,3点を結んで直径となる場合なのですが,「直径」あるいは「線分」も,図形であるかどうかは,『小学校学習指導要領解説算数編』『算数教育指導用語辞典』を読んだものの,明らかにされていません.そういった厄介な話を排除するという意味でも,「図形は,どんな図形」よりも「三角形は,どんな三角形」のほうが小学生向けの出題と言えます.