わさっきhb

大学（教育研究）とか ，親馬鹿とか，和歌山とか，とか，とか．

かけ算の式と言葉の順序 メモ

5×3 reprise

1. Nunokawa (2010)

Students are required to clearly distinguish between multiplicands and multipliers at this stage because this distinction helps them understand the meaning of multiplication. Teachers pay attention to whether their students understand that multiplicands express sizes of units and multipliers express numbers of groups. These meanings are reversed from the viewpoint of some educators elsewhere in the world. The amount of oranges in Figure 1 is expressed as 4×6＝24 in Japan. The expression 6×4 is not usually allowed at the introductory stage.
(p.122)

この中の"These meanings are reversed"に，戸惑いを覚えました．これらの意味は逆になる…かけられる数とかける数の意味が逆になる，とは?
対応する日本語は，「ただしこの意味は世界共通でなく，例えば英語ではこれを6×4＝24とするので，被乗数，乗数の意味は逆になる．」(p.50)です．素直に解釈すれば，日本の4×6＝24は，英語では6×4＝24と書くのだよ，となります．
これまでに書いてきたことと，新たに読んだことを整理し，日本語・英語・他の言語での，かけ算の式と言葉の対応関係について，調べてみました．

2. Yoshida (2009)

  • Yoshida, M. (2009). Is Multiplication Just Repeated Addition? ― Insights from Japanese Mathematics Textbooks for Expanding the Multiplication Concept, 2009 NCTM Annual Conference. http://www.globaledresources.com/resources/assets/042309_Multiplication_v2.pdf（デッドリンク）

タイトルを訳すと「かけ算は累加でいいの? ― 日本の算数教科書に見る，乗法概念の拡張の考察」でしょうか．NCTM（National Council of Teachers of Mathematics, 全米数学教師協議会）の口頭発表用スライドです．
かけ算の式の意味を，次のように記しています．

  • Multiplication sentences describe equal set situations.
    • Repeated addition and skip counting are ways to find the total (product).
  • The numbers in a multiplication sentences mean something specific:
    • Number in a group - multiplicand
    • Number of groups - multiplier
    • Total number of objects - product
  • （かけ算の式は，それと数の等しい，決まった状況を表す．
    • 累加や，まとめて数えることは，いずれも総数（積）を求める方法である．
  • かけ算の式に現れる数には，明確な意味がある．
    • 1つのグループに含まれる数＝かけられる数
    • グループの数＝かける数
    • 対象の総数＝積）

(p.11)

3. Multiplication - Wikipedia

Yoshida (2009)は，Wikipedia:en:MultiplicationのNotesの1番目で，かつてリンクされていました．その本文は次のとおりでした．

Multiplication (often denoted by the cross symbol "×") is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic (the others being addition, subtraction and division).
Because the result of scaling by whole numbers can be thought of as consisting of some number of copies of the original, whole-number products greater than 1 can be computed by repeated addition; for example, 3 multiplied by 4 (often said as "3 times 4") can be calculated by adding 4 copies of 3 together:
3 × 4 = 3 + 3 + 3 + 3 = 12.
Here 3 and 4 are the "factors" and 12 is the "product".
Educators differ as to which number should normally be considered as the number of copies, and whether multiplication should even be introduced as repeated addition.[1] For example 3 multiplied by 4 can also be calculated by adding 3 copies of 4 together:
3 × 4 = 4 + 4 + 4 = 12.
（かけ算（よくバツ印「×」で表される）は，一つの数を他の数で拡大するという，数学の演算である．それは小学校の算数で学習する，四則演算の一つである（残りはたし算，ひき算，わり算）．
整数による拡大の結果は，もとになるものに対するある数のコピーと考えられるので，1より大きい整数の積は，累加によって求められる．例えば，3に4をかける（「3かける4」ともいう）と，3の4つのコピーを足し合わせることで計算できる：
3×4＝3＋3＋3＋3＝12
このとき，3と4は「因数」，12は「積」という．
どちらの数がコピーの数になるか，またかけ算は累加で導入するのでいいのかについて，教師らは見解が一致しない[1]．例えば，3かける4は，4の3つのコピーを足し合わせて計算することもできる：
3×4＝4＋4＋4＝12）

"original"の数が，かけられる数で，"copy"の数が，かける数です．multiplicandとmultiplierは，少し下に書かれていました．

The numbers to be multiplied are generally called the "factors" or "multiplicands". When thinking of multiplication as repeated addition, the number to be multiplied is called the "multiplicand", while the number of multiples is called the "multiplier". In algebra, a number that is the multiplier of a variable or expression (e.g., the 3 in 3xy^2) is called a coefficient.
（かけられるほうの数は一般に，「因数」または「かけられる数」と呼ばれる．かけ算を累加で考えるとき，かけられるほうの数を「かけられる数」，複製の数を「かける数」という．代数では，変数または式における乗数（例えば3xy^2における3）は係数と呼ばれる．）

4. Greer (1992)

  • Greer, B. (1992). Multiplication and Division as Models of Situations. In Grouws D.A. (Ed.): Handbook of Research on Mathematics Teaching and Learning, National Council of Teachers of Mathematics, pp.276-295. [isbn:1593115989]

式を使わずに，かけ算が用いられる場面，そして乗数・被乗数を説明しています．

A situation in which there is a number of groups of objects having the same number in each group normally constitutes a child's earliest encounter with an application for multiplication. For example,

3 children have 4 cookies each. How many cookies do they have altogether?

Within this conceptualization, the two numbers play clearly different roles. The number of children is the multiplier that operates on the number of cookies, the multiplicand, to produce the answer. A consequence of this asymmetry is that two types of division may be distinguished.
（いくつかのグループがあって，各グループで同じ個数のモノがあるときというのが，子どもが最初にかけ算を用いる場面になる．例えば

3人の子どもが4つずつクッキーを持っている．全部合わせるとクッキーは何個か？

これをかけ算の式で表そうとするとき，2つの数は明らかに異なる役割を担っている．子どもの数は「乗数」であり，クッキーの数すなわち「被乗数」に作用して，答えとなる総数が得られる．この非対称性から言えるのは，2種類のわり算を考えることができてそれぞれ区別されるということである．）
(p.276)

ただし上記は，かけ算の導入としてよく用いられるタイプであり，小学校で学習するかけ算のすべてではありません．「乗数と被乗数を区別しない文脈」の説明もあり，そこでは，m×nというかけ算の式が出てきます．

Cartesian products provide a quite different context for multiplication of natural numbers. An example of such a problem is

If 4 boys and 3 girls are dancing, how many different partnerships are possible?

This class of situations corresponds to the formal definition of m × n in terms of the number of distinct ordered pairs that can be formed when the first member of each pair belongs to a set with m elements and the second to a set with n elements. This sophisticated way of defining multiplication of integers was formalized relatively recently in historical terms.
There is a symmetry between the roles of the two numbers here, and hence only one type of division problem. Given that there are 12 possible partnerships, there is no essential difference between (a) being told that there are 4 boys and asked how many girls there are and (b) being told that there are 3 girls and asked how many boys. (In fact, it would be unusual to pose division problems of this type.)
（デカルト積は，自然数の乗法に対してまったく異なる文脈を与える．例題を示す．

4人の男の子と3人の女の子がダンスをするとき，男女のペアは何通りできるか？

一般化すると，順序対の総数を求めようということである．その際，各順序対の最初はm個の要素からなる集合に，また2番目はn個の要素からなる集合に属する．そうすると，総数はm×nで表される．このような整数の乗法の定義は，比較的最近になって，歴史的な観点でなされるようになった．
この場合，×の前後に書く2つの数の役割は対称性を持ち，したがって除法の問題は1種類だけとなる．男女のペアは12通りであることを前提として，「(a) 4人の男の子がいるとき，女の子は何人いるか？」と「(b) 3人の女の子がいるとき，男の子は何人いるか？」との間に本質的な違いはない．（とはいえ，こんな形のわり算の問いを出題するのは普通じゃないんだけど．））
(p.277)

こちらの説明では，かけ算の式がある一方で，「乗数」「被乗数」に相当する言葉が出てきません．これは，デカルト積に基づくかけ算の特徴と言ってよさそうです．

"relatively recently historical terms"，「比較的最近になって，歴史的な観点で」というのは，直後のAnghileri & Johnson (1988)，後ろの中島(1968)によると，SMSG（School Mathematics Study Group，学校数学研究グループ）ではかけ算の意味づけに，デカルト積と密接な関係を持つ，アレイを使用していることを指しているようです．

5. Anghileri & Johnson (1988)

  • Anghileri, J. and Johnson, D.C. (1988). Arithmetic Operations on Whole Numbers: Multiplication and Division. In Post, T.R. (Ed.): Teaching Mathematics in Grades K-8, Longman Higher Education, Allyn and Bacon, pp.146-189. [asin:0205110762]

整数を対象としたかけ算・わり算の解説です．
3×4の読み方そして意味には，"3 multiplied by 4"，"3 times 4,"，"3 fours"の3種類があるとしています．

When considering how the symbolic expression 3×4 is interpreted by adults and children, we find the most common expressions are "3 multiplied by 4," "3 times 4," and "3 fours." Some people will use the expressions quite interchangeably on the understanding that all three are equivalent; in the domain of mathematics this may be acceptable but in real life there is an important distinction between these different interpretations. On one hand "3 times 4" and "3 fours" usually relate to three sets of four objects and are consistent with "3 lots of 4."
For children, three lots of four and four lots of three are fundamentally different. They think in concrete terms---three children each having four candies are luckier than four children each having three candies although the total number of candies is the same.
（3×4という式が何なのか，大人と子どもが説明すると，たいてい「3に4をかける」「3倍の4」「3つの4」のいずれかとなる．これら3つの解釈を同じものとして理解し，どれを使っても変わりがないように，3×4という式を使う人もいる．数学的には，その扱いで問題ないかもしれないが，日常生活においては，これらの解釈には大きな違いがある．「3倍の4」と「3つの4」は普通，4つのモノからなる集合が3つある状態に関連づけられ，「4が3つ」に対応する．
子どもたちにとって，「4が3つ」と「3が4つ」は基本的に別物である．具体物で考えると---4つずつキャンディを持っている3人の子どもは，3つずつキャンディを持っている4人の子どもよりも，運がいい．キャンディの総数は同じなのだけれども．）
(p.157)

「大きな違い」というのは，「"3 multiplied by 4"」と「"3 times 4"と"3 fours"」の間の違いと思われます．ただし，"3 multiplied by 4"については，特別な記述は見当たりませんでした．
For childrenから始まる段落については，かけられる数もかける数も，式も出てきませんが，4×3と3×4の違いを説明したものになっています．乗法の交換法則の説明も同様で，次のようになっています．

The balance or symmetry in the multiplication square relates to a very important property called the commutative property of multiplication, which states that for any two numbers a and b, a×b＝b×a (for example, 3×4＝4×3). Note that this is a property of numbers. While it is true that 3×4 is equal to 4×3, 3×4 may not be the same as 4×3 in a real-life situation.
（かけ算の表の釣り合いや対称性は，乗法の交換法則と呼ばれる重要な性質に関連している．すなわち，任意の2つの数aおよびbに対して，a×b＝b×aである．例えば3×4＝4×3となる．注意しないといけないのは，これは数の性質ということである．3×4が4×3と等しいのは事実だが，日常生活においてそれらが同じであるというわけではない．）
(p.177．強調は原文では斜体)

6. Davies (1841)

1841年の本というのは，わくわくします．ともあれ，かけ算の定義，かけられる数とかける数から，確認しました．

Multiplication is a short method of repeating one number as many times as there are units in another.
The number to be repeated is called the multiplicand.
The number denoting how many times the multiplicand is to be repeated, is called the multiplier.
The number arising from repeating the multiplicand as many times as there are units in the multiplier, is called the product.
The multiplicand and multiplier are called factors, or producers of the product.
The sign ×, placed between two numbers, denotes that they are to be multiplied together. It is called, the sign of multiplication.
（かけ算は，一つの数を，もう一つの数の数だけ繰り返すことの簡潔な方法である．
繰り返される数のことを，かけられる数という．
かけられる数が何回繰り返されるかを表した数を，かける数という．
かけられる数を，かける数の回数だけ繰り返すことで生じる数は，積という．
かけられる数とかける数は因数，あるいは積を生成するものと呼ばれる．
記号×は，2つの数の間に置かれ，それらをかけ合わせることを表す．これは乗算記号と呼ばれる．）
(p.42)

p.44では，かけられる数を「×」の左に，かける数を右に置く式が見られます．
間のpp.43-44に，"1 times 0 is 0"から"12 times 12 is 144"までの，かけ算の表があります．timesを前置詞と見ると，その左に書かれる数がかけられる数，右がかける数です．
ところで，p.44，EXAMPLESの1の最後に，"... the number arising from repeating 4 two times."とあります．two timesが「2回」という副詞句になり，repeatingを修飾します．ということは，かけ算の表のa times bも，もしかしてaがかける数（今の英語と同じ）になるのかな，と思ったものの，two timesと4との間には係り受けの関係がないので，別扱いとしてよさそうです．

7. Ask Dr.Math

2001年のフォーラム（電子掲示板）の質問・回答です．「456 x 10」と書くとき，「456がかけられる数，10がかける数」なのか，それとも「456がかる数，10がかけられる数」なのかという質問に対して，回答者(Doctor Peterson)はまず，そんなのどっちでもいいんだよ，"factors"（因数）と呼べばいいんだから，としています．
しかし第2段落は，面白い内容を含んでいます．

I recently saw a facsimile of a 19th-century text that defined the multiplier as the SMALLER of the two numbers, regardless of the order. So there's yet a third definition to use.
（最近，19世紀の文書の複製を見ることがあって，そこでは，2つの数のうち小さい方を，かける数と定義していた．なので3番目の定義もあるってこと．）

目を引くのは，"regardless of the order"という表現です．英語でも，「かけ算の順序」のあるなしを，言ってよさそうです．
それと別に，小さい方がかける数というのは，半九九を連想します．回答者がどんなのを見たのか，不明なのが残念ですが．

8. Math Solutions

  • http://www.mathsolutions.com/index.cfm?page=wp10&crid=137&contentid=463（デッドリンク）

質問の大要は，Ask Dr.Mathと同じです．20 x 5 = 100と書いたとき，"multiplier x multiplicand = product"なのか，それとも"multiplicand x multiplier = product"なのか，です．
Marilyn Burnsの回答は，交換法則があるから，どっちだっていいんだよ，から始まります．
20 x 5を表す言葉に，"20 groups of 5"，"twenty 5s"のほか，"20 five times"というのもあります．
しかし，"twenty $5 bills"を例に挙げて，式表現の注意を喚起しています．経営数学の教科書で"multiplicand x multiplier = product"を採用しているのなら，式は5 x 20です．
"Neither is more precise or accurate than the other."は，「かける数×かけられる数＝積」と「かけられる数×かける数＝積」との間で，どちらが正しい（正確・適切である）というものではない，といったところでしょうか．

9. 中島(1968)

ここから，日本人が書いたものを取り上げていきます．

論争というのは米国の話です．日本では，乗法を加法の特別な場合を簡潔に表わすという立場から意味づけており，乗数が有理数になる場合には，割合の考え，すなわち「A×BはAという単位量のスカラー倍」によって，意味を拡張することを述べています．
「参考文献」として9項目あるうちのいくつかに，式表示の注意書きが記されています．

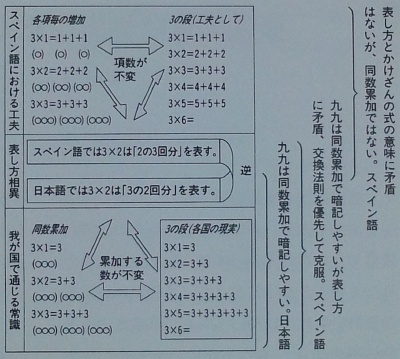
4) 4×2は，英語ではfour times twoまたはfour twosなどという関係で，乗数と被乗数がわが国の場合と反対になっている．
8) 以下では，乗数，被乗数の順については，わが国の表記による．
9) (略)なお，註4)で，アメリカでは，乗数を先にかくとのべたが，最近では，わが国の場合のように，乗数をあとにかく方法（乗数をoperatorとしてみる場合に統一的にでき便利である）をかなり取り入れるくふうがされている．この場合，3×4は3 multiplied by 4などと呼んでいる．
(p.77)

10. 森(1977)

この文章，「かけ算の順序論争」としてだと，見るべきなのはまず，出だしの「掛け算事件」であり，次に，大学入試ではトランプ配りを答案にどう書くべきなのかを提示しているところでしょう．
ですがそれらの間に，日本とヨーロッパとの，式の違いのことが記されています．

じつは，少しも「掛け算の意味」を教えていなかったところが学校側の問題なのだが，親の方もいくらかヘンなところはある．この，4×6とか6×4とかいった順序は，日本とヨーロッパでは違う．日本は「4の6倍」式に4×6と書くが，ヨーロッパでは「6倍の4」式に6×4と書く．これは左側通行か右側通行かみたいなもので，言語習慣から来ている．ただし，日本式の方が合理的というのが世界の相場だが，一方ではヨーロッパ式の方がすでに流通してしまっている．まあ，これはヤクソクには違いない．足すを＋と書き，掛けるを×と書くようなのもヤクソクで，これを勝手に変えたら混乱してしまう．
(p.67)

11. 木村(1936)

  • 木村教雄 (1936): 小学算術教材ノ基礎的研究, 培風館.

(略)
斯様にして，欧米諸国の掛算九九は何れも被乗数先唱であり，我国の実際家にも此の被乗数先唱が便利であるとする者が相当に多い．併し之に対して乗数先唱の利点もまことに注目すべきものであって，我国小学国定算術書は被乗数先唱を採用して居る1)．
(p.23)

欧米諸国がどうなっているかは，本からは見られません．なお，「1)」に関しては脚注に，大正十四年度修正趣意書への参照をつけています．黒表紙・緑表紙の違いなどを考慮すると，「我国小学国定算術書は乗数先唱を採用して居る」が真意ではないかと推測します．

12. 馬場(2002) - タイ

この報告書の目的は，目次の直後，要約のところで，「本報告書では、近年盛んに行われている民族数学研究の整理を通して、数学教育協力の中で特に数学教育のもつ文化的側面を考察する」と示されています．
文化もしくは認識構造の違い(p.35)について，かけ算で例示しています．

ここで問われているのは、先のA型の問題ではない。その意味で教授言語が母語であるとしても、この種の問題が起きないとはいえない。例えば、英語で高等教育を受けた人が帰国して、その国の言語でカリキュラム開発を行う場合を考えるとすると、文化的認識の差異を意識することなしに、元は英語で作成された学習指導要領、教科書などをそのまま翻訳してしまう場合などはB型の問題を含んでいる可能性がある。
具体例を挙げて、少し説明を加える。かけ算の導入は、日本では次のように扱われる。
『しょうがくさんすう2年下』（中原他, 1999, p.16）
みかんがひとさらに5こずつのっています。4さらではなんこになりますか。
この問いに対して、1さらに5こずつ4さらぶんで20 こです。このことをしきで
5×4＝20
とかき「五かける四は二十」とよみます。
それに対して、英語ではかけ算を表す順序が逆で、“four plates of 5 oranges”という英語での表現より、4×5＝20となる。そこで問題となるのは、例えばタイでは自然な語順が日本語式であるにもかかわらず、教科書は英語式の順番に従っている。単にかけ算の順序が逆になっただけで小さなことのようであるが、初めての学習者にとってはかなりの認知的な負担が強いられるだろう。この例に見られるように、認識的な差異を考慮に入れないでカリキュラム開発をするならば、教科書という基本的な教材の中に、基本的な問題を抱えこんでしまう可能性がある。
(pp.37-38)

表にしてみます．

　 語順 かけ算の順序
日本語 かけられる数が先 かけられる数が先
英語 かける数が先 かける数が先
タイ語 かけられる数が先 かける数が先

しかしこのギャップに注意した上で，タイの算数で，かけ算の式を「かけられる数が先」にしていいのかどうかについては，要検討なようにも思います．

13. 柳原(2008) - フィリピン

かけ算について，語順の和英比較そしてフィリピノ語での表現は，次のとおりです．

表2は、教授言語（第二言語）による数学（算数）学習の問題例である。例えば、(1)英語で「One plus one equals two」（1、＋、1、2の語順）は、日本語では「1と1をたすと2」（1、1、＋、2の語順）である。(2)英語で「Two times three equals six」（2、×、3、6の語順）は、日本語では「2と3をかけると6」である。(3)英語で「Two thirds」と分子（基数）、分母（序数）の順に対して、日本語は「3分の2」と分母（基数）、分子（基数）の順である。これら語順のみを取り上げても、教科書の教授言語の語順が母国語で培ってきた自然な語順と違っている場合、初めての学習者にとってはかなりの違和感であろう。

(p.137)

因みにフィリピノ語は次のような語順であり、これに関しては英語と変わらない。(略)
(2) 2×3＝6 → dalawa pinarami ng tatlo ay anim
　　　　（2）（×）（〜を）（3）（は）（6）
(p.138)

柳原(2008)は，先ほどの馬場(2002)を引用しています．「教授言語におけるB型の問題」(p.135)や「認識構造」(p.139)が特徴的です．
そしてこの文献は，昨年2月，2箇所で別々の主張のために，リンクされています．

リンクの意図は，それぞれ異なります．前者は，「こういう様々なところに現れる言語の多様性/複雑さを捨象して、語順と「ひとつあたりの数」/「いくつ分の数」の順番を強く関係付ける議論はちょっと乱暴に思えちゃいます」が主張の中核となりそうです．後者は，数学教育に関わる人々は，文化についても配慮しているのだよという指摘です．

14. 細水(2011) - イスラエル

1つ目の巻き物を出し，ゆっくり広げていく。広げ終わった途端，多くの手が挙がった。

1＋2＋3＋4＋5＋6＋7＋8＋9

(p.48)

その眼はどこかで見たことが。そう，日本の子どもたちと同じ眼をしている。知りたい，わかりたいという知的好奇心，伝えたいという気持ちを持った眼である。
（図省略）
4×10＋5＝45（日本では10×4＋5であるが）
「日本の先生のクラスの子は，5×9＝45と計算して求めたけれど，どうやって考えたかわかるかな？」
と問いかけた。
パラパラ手が挙がり始める。隣同士相談しても良いことにすると，仲良く話し合う姿が見られた。
5×9＝45（日本では9×5＝45であるが）
（図省略）
(同)

15. 磯田 (2012) - スペイン


(p.11)

16. ドミニカ共和国

日本と中南米では、まずかけ算の基本的な部分に大きな違いがあります。日本では「個別量×数量」という考え方をしますが、中南米ではこれが逆になって「数量×個別量」になります。具体的に言うと、例えば「1袋5個入りのパンを3袋買いました。全部で何個のパンを買ったでしょう。」という問題があった場合、日本では“5×3”ですが、中南米では“3×5”になります。かけ算は交換法則（乗数と被乗数を入れ替えても積は変わらない）が成り立つのでどっちでもいいじゃないかと思うかもしれませんが、これが授業をおこなう上で大問題となります。

17. 大田(1992) - 東ドイツ

東ドイツの教科書は，1年生で［20までのかけ算］を扱う。ここでは，2＋2＋2＝6を2・3＝6としている【図6】。ここでの乗数と被乗数の順序は日本式である。ところが2年生の教科書では，2＋2＋2＝6が3・2＝6と，欧米式の順序になっている【図7】。ドイツ語で3・2は“drei mal zwei（3つの2）”であるから，後者が自然である。もっとも，東ドイツの教科書は交換法則を強調しているから，どちらでもよいといえばそれまでであるが。
(p.172)

図6，図7はp.173で横並びになっています．「かけられる数」「かける数」に対応しそうなドイツ語は読み取れませんでしたが，図6で，3と2を囲っている中の"Faktor"は，"factor"すなわち「因数」のことでしょう．
図6中段の「2＋2＋2＋2＝8（2・4＝8）」と「4＋4＝8（4・2＝8）」については，場面に対応する式が一つずつです．
図6の馬，そして図7の行楽については，日本でも，かけられる数とかける数を交換した2つのかけ算の式が，正解になりそうです．それは「交換」というよりも，「一つ分の大きさ」が2種類選べて，一つ選べば「いくつ分」も決まるからです．デカルト積のピクトリアルに載せた「ふしぎな花のさく木」「お菓子」が該当します．

18. まとめ

日本語・英語・他の言語での，かけ算の式と言葉の対応関係について，集約を試みました．
これらから，かけ算の「意味」と「構文」を再確認できました．まず「意味」については，「被乗数と乗数のペア」という，区別される2つの数量によって積を求める場合（倍の乗法）と，2つの「因数」による，実質的な区別のない2つの数量によって積を求める場合（積の乗法）に大別されます．東ドイツで最後に書いた，一つの場面で複数の被乗数（一つ分の大きさ，original）を発見できるシチュエーションというは，倍の乗法と積の乗法のつなぎ目のような存在です．
「構文」についても，基本となるのは「被乗数×乗数」と「乗数×被乗数」の2種類です．日本の算数では，「被乗数×乗数」で一貫していると言っていいでしょう．しかし英語になると，"3 times 4"は「乗数×被乗数」ですが，Davies (1841)のころは「被乗数×乗数」だったのを，うかがい知ることができます．"3 multiplied by 4"は2数の関係から「被乗数×乗数」と理解している人も，"3 times 4"と同義ということで「乗数×被乗数」扱いする人も，いるように思います．
こうしたとき，「適切な式」「正解となる式」を支えているのが，その状況での「構文」と「意味」です．会話する人どうしで，学校なら先生と児童の間で（ときには子どもたちどうしでも），意味すなわち何の話なのか，構文すなわち何に当てはめて表現するのかを，外から観察する者として，一つ一つ，見ていくというわけです．
Math Solutionsの件は，「学校教育のかけ算は，ビジネスの常識と違う」となります．その一方で，「ビジネス（あるいは社会）の慣習を，学校教育のかけ算に押しつけていいのか」についても，よく考えていかないといけませんね．

案内所

  1. 過去に書いたこと
  2. もっと長文
  3. 資料集
  4. 遠山啓
  5. 学校をはなれて