雑報です.1957年の本から1冊,2013年の本から2冊,そして昨日実施された,全国学力テストの問題を,取り上げることにします.
1. 算数科の教育心理

- 出版社/メーカー: 金子書房
- 発売日: 1957
- メディア: ?
- この商品を含むブログ (15件) を見る
- 中野佐三(編): 算数科の教育心理, 児童心理選書 第八巻, 金子書房 (1957).
Amazonマーケットプレイスで購入した本では,奥付に「昭和三十二年五月廿五日 初版発行」「昭和五十一年十一月十五日 十六版発行」「©1975」と書かれています.最後は「©1957」の誤りと思われます.
この中に,「かけ算の順序」に関係する2種類の指導例があります.簡単にいうと,3年生の指導では,ある文章題にa×bの式のみを正解としているけれど,4年生の指導では,a×bだけでなくb×aも正解としています.
三年の指導
1. 必要な条件を抜き出して書かせる指導
問題1 おかあさんが,びわをおぼんにのせて,ぼくたち7人に下さいました。1人が6つずつたべたら,ちょうどなくなりました。はじめに,びわはいくつあったのでしょう。
問題2 はこづめのいちごがならべてあります。1つのはこには5こずつ,4れつにはいっています。いちごのかずはどれだけでしょう。
以上の問題を三年生の42名に回答させた。問題(2)では,ほとんどの子どもが5×4=20と正しく式に表現し,被乗数と乗数とを反対にして4×5=20としたものは,僅かに2名であった。問題(2)に対して問題(1)では,6×7=42としたものが22名で7×6=42と被乗数と乗数とを逆に書いたものは18名の多きに達した。その理由を探求してみると,乗法の文章題として与えられる問題は,問題(2)の形式の類が多くドリルさせられ,問題(1)の形式の類はその練習度が少ないので,しらずしらずの中に,乗法の問題では,文章中の初めに出て来た数を被乗数に,後から出て来た数を乗数にしたらよいのだというふうになっているからではないかということが考えられた。いいかえると,深く問題を読むことなしに,誤った先入観によって式化してしまう悪習慣がついているからであろうと思えた。
そこで,問題を深く読み,乗数と被乗数とを正確に理解させるために,つぎのようなことをした。
- さんすうのテストで3つまちがいました。1つ5てんびきだそうです。なんてんひかれるでしょう。
- こたえのめいすう……いくつ,なんてん
- かけられるかず……( )
- かけるかず……( )
答えの名数の正しいところを,○印でかこませ,かけられる数,かける数を記入させて立式させるようにした。
その結果,在籍42名中,被乗数と乗数とを逆にして式を立てたものは,僅かに5名であった。しかも,5名中,全部の問題(4題提出)を誤ったものは1人もなく,3問まちがったもの1名,あとは1問だけ誤っていた。一応成功したといってよいのである。
(pp.137-138)
2. 四年生の指導例
4年1組45名で,こう堂にいすをはこんでいます。1人が1こずつ4かい運ぶと,みんなでいすは,なんこ運ぶことになるか。
黒板に出てした子どもの解法には2つの型があった。
A 4こ×45=180こ
B 45×4=180
Aは正解であるが,Bは間違っているという意見が出て討論がはじまった。
「Aなら意味がわかるけど,Bでは意味がわかりません。45は人数だから180人になります。」
「Bでも180こになります。」
と2〜3の子どもが主張したが,根拠が薄弱でみんなを納得させることができない。そこで,教師はAの解法の意味をつぎのようにおさえさせた。4こ × 45=180こ……全体で運んだ数 ↓ ↓ 一人が運ぶ数 人数「Aの解き方が正しいことはわかりましたね。こんどはBの解き方がほんとうに間違っているのか。正しいとしたら,なぜ正しいのか。問題を読んで,1つ1つの数に当って,その意味をしっかり考えてごらん。」子どもたちはとうとう発見した。
45こ × 4=180こ……全体で運んだ数 ↓ ↓ 全体が1回 回数 に運ぶ数T「Aの解き方とBの解き方と,どう違うのでしょう。」
P「解く前の考え方がちがいます。」
A,Bの解き方を比較して話し合いながら,問題をとくときの大切な考え方として,つぎのようにまとめた。
- 見とおしをつける。
- それから計算にうつる。
A,Bの見とおしのつけ方のちがい。
A 1人が運ぶ数を考える。それを人数倍したら全体の数がでる。
B 1回にみんなが運ぶ数から考える。それに回数をかけると全体の数が出る。
この指導の後で,1日おいて次の問題を,見透しをまずノートに書いてから立式するように指導した。
四年生96名で,こう堂にいすをはこんでいます。1人が2こずつ4かい運ぶと,みんなでいすは,なんこ運ぶことになりますか。
1つの観点で解決に成功した子どもには,別な観点で解くように指示した。子どもたちが意識して見透しをつけるようにするためには,観点をたてることの指導の最初の段階において,教師は適切な指示を怠ってはいけない。このように観点をたてることの指導は,数の働きがわかることを基礎として,立式指導に関連させ,多方的解法をさせることによってその効果をあげることができる。
(pp.151-152)
前後も含めて読みたい方へ.本を手に入れなくても,汝の隣人のブログを愛せよ | LOVELOGでページの画像が張られています.「かけ算の順序」を学ぶための本など - Togetterには,今年1月の情報交換を保存しています.
3年生と4年生とで,なぜ正解基準が異なるかですが,真っ先に思い浮かぶのは次の文章です.
乗法の場面、「1ふくろにミカンが3こずつ入っています。5ふくろでは、ミカンは何こでしょう。」は、3×5と立式される。立式は、「1つ分の数×いくつ分=全体の数」とまとめられ、それぞれ被乗数、乗数という。ところで、「オリンピックの400メートルリレー」や「このDVDは16倍速で記録できる」、「xのk倍は」の式は、どのように表わされるであろうか。それぞれ、一般的には「4×100mリレー」、「16×」、「kx」と表される。被乗数と乗数の位置が教科書の書き方と逆になっていることに気付くであろう。この例から分かるように、乗法では、数の位置ではなく、数が意味する内容に注目して、どの数が1つ分の数であるか、いくつ分はどの数かをしっかりと読み取ることが大切である。第2学年や第3学年では、読み取った数を、「1つ分の数×いくつ分=全体の数」と表現できることが重要であり、逆に、この立式ができているかで、数の読み取りができているかを判断できる。しかし、高学年になり、乗法では交換法則が成り立つことや外国での立式を知り、数の意味をしっかり理解できていれば、必ずしも第2学年で学んだ順序で立式することを強制しなくてもよい。
(『小学校指導法 算数 (教科指導法シリーズ)』pp.91-92.転載元)
50数年前も,現在も,低学年・高学年で基準が異なっていていいのだ,と思ってよさそうです.
ところで四年生の指導例のうち,「B 45×4=180」に「45こ×4=180こ」という解釈を与える話は,『数の現象学 (ちくま学芸文庫)』pp.67-68と同じです.上に引用した事例だと,問題文の「45名」(45人)を,全体が1回に運ぶ数として「45こ」に転換することが必要となります.
その際,「式に単位をつけるべきか」の確認もしておかないといけません.1957年発行の今回の本,1961年と1971年の2種類の『水道方式入門』,そして読んできた本やWebの情報を総合すると,戦後すぐの算数では,かけ算の式に「4こ×45=180こ」「45こ×4=180こ」と,かけられる数には単位(助数詞)名数を添え,かける数には添えないという式の書き方が,広く認められていたようです.
現在はどうかというと,算数の授業では,数教協スタイルの本で「4こ×45=180こ」や「4こ/人×45人=180こ」の表記を見かけることもありますが,教科書を含め多くが「4×45=180」と,単位なしです.その一方で,学校を出てみると,「4個×45人=180個」と,かける数にあたるものにも単位がつくのが,当たり前になっています.メールでは「45人×4個=180個」と同型の式を受け取ることもあります.
「式に単位をつけない」ことを前提とすると,次のやりとりを生むことになります.「4年1組45名で,こう堂にいすをはこんでいます。1人が1こずつ4かい運ぶと,みんなでいすは,なんこ運ぶことになるか。」の問題文で「45×4=180」と書いた子には,「それだと45人が4つで,180人になっちゃうよ」と言うことができます.上の引用でも,討論の中で「45は人数だから180人になります。」という発言があります.この考え方は,古くは1951年(昭和26年)の学習指導要領試案,平成に入ってからも『板書で見る全単元・全時間の授業のすべて 小学校算数2年〈下〉』や『新版 小学校算数 板書で見る全単元・全時間の授業のすべて 2年下』で,同様のことが書かれています.
別の解釈もできます.「45×4=180」という式は,「4人が1こずつ45回運ぶ」という意味になってしまう,というものです.そのような解釈の事例は,2冊の『板書で見る…』のほか,asahi.com(朝日新聞社):2×8ならタコ2本足 - 花まる先生公開授業 - 教育にも見ることができます.
書いた子が,「1回にみんなが運ぶ数から考える。それに回数をかけると全体の数が出る。」と考えて,45×4=180と書いたとしても,「それだと180人になっちゃうよ」「4人が45かいになるよ」の指摘は成立します.
a×bを期待するところで,b×aの式がどのように解釈できるかについては,式を読み取る練習で整理を試みました.直近の検討としては,子どもたちは,問題解決型の授業で,「式」から「考え方」を推定しているをご覧ください.
2. 算数の学習プリント

算数の学習プリント―学力調査・算数的リテラシーに対応! (教育技術MOOK)
- 作者: 吉川成夫
- 出版社/メーカー: 小学館
- 発売日: 2013/04/06
- メディア: ムック
- この商品を含むブログ (9件) を見る
[もんだい1] つぎのもんだいがあります。
4つのプランターに3つずつチューリップのきゅうこんをうえます。きゅうこんはなんこいりますか。
①たし算の式で答えをもとめましょう。
式 答え
②かけ算の式で答えをもとめましょう。
式 答え
(p.33)
「4つのプランターに…」は,よく目にする,基準量が後に示された問題です.
特色は,先にたし算の式を書かせるところにあります.図を実際に描くなり,頭の中で思い描くなりして,式は3+3+3+3=12,答えは12こを得ます.ここで4+4+4=12と書いたら,プランターが12個になっちゃうよとなります.
次にかけ算ですが,たし算の式を先にやっているので,3×4=12の式へとつながります.答えはたし算で求めても,かけ算で求めても,同じ12こです.①と②の比較によって,かけ算のほうが簡単に書けていいねと見ることもできます.
同じページの下には,[もんだい2]として,①6×4,②4×6,の作問があります.3年に上がっても,p.40の「わり算の式」で,12÷4という式と,けんとさん・あやのさんという2人の問題を見て,たしかめの式が「□×4=12」と「4×□=12」から選ばせるというものもあります.
4年で「どちらでもいい」を見かけました(p.54).
○○○○○○ ○○○○○○ ○○ ○○ ○○ ○○ ○○ ○○
という配置があって,○の総数を求めること…が問題ではなく,式が添えられています.4人の子どもたちの式があって,①は10×2+4です.「どのように区切って考えたのでしょう。区切りの線をかきましょう」と出題しています.
それを踏まえて,次の問題です.
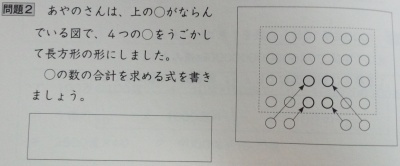
長方形配置だから,4×6でも6×4でもいいはず…解答を見ると(p.115),「4×6または6×4」となっていました.
3. 中1ギャップ撃退トレーニングワーク

数学科 中1ギャップ撃退トレーニングワーク 算数のつまずきを6時間で克服する本
- 作者: 川上公一
- 出版社/メーカー: 明治図書出版
- 発売日: 2013/03/04
- メディア: 単行本
- この商品を含むブログを見る
本のどこにも,□×△が正解で△×□は不正解とするような出題は,ありません.
「文字を使った式」のところが,興味深かったのでした.
[チェック問題]
1本50円の花x本に80円のリボンをつけてもらって花束をつくります。
(1)花束の代金の合計を式に表すと,
( )円になります。
(p.26)
[トレーニング問題]
①〜④の場面について,xとyの関係を式に表しましょう。
①底辺がx cm高さが5cmの三角形の面積は,y cm^2です。
xとyの関係を式に表すと,( )になります。
②3Lのお茶があります。x L飲むと,残りはy Lです。
xとyの関係を式に表すと,( )になります。
③x kgのりんごを0.6kgの箱に入れると,全体の重さはy kgになります。
xとyの関係を式に表すと,( )になります。
④10個でx gの1個の平均の重さはy gです。
xとyの関係を式に表すと,( )になります。
(同)
加減乗除1問ずつです.しかし①では「2で割る」必要がありますし,②は,3−xかx−3かで,少し迷いそうです.
解説も書き出すことにします.
文字を使って式をつくるとき,その表し方は1通りではありません。例えば「②3Lのお茶があります。x L飲むと,残りはy Lです」の場面では,x+y=3やx=3−yでも,xとyの関係を表す式になっています。図で考えるとよくわかります。(図は省略)
(p.27)
指導に当たられる先生へ*1
小学校では,求めたいものがあるときは,○や□を使って数量の関係を表す式をつくり,○や□に当てはまる数を求めます。この考え方は3年から用いられているため,なじみのあるものです。
6年では,数学における文字の式の学習の素地として,数量を表す言葉や□,△などの代わりに,a,xなどの文字を用いることを学習します。文字が本格的に使用されるのは中学校からですが,算数と数学とのなだらかな接続という観点から,小学校でもa,xなどの文字を使って式で表すことのよさを味わえるようにしているのです。
中学校では,文字や文字の式を用いて,数量やその関係を簡潔・明瞭に,しかも一般的に表現することが求められます。そのためには,文字を用いて式を表すことのよさを感得しておくことが大切です。
小学校学習指導要領の算数編では,式の働きとして次の4つが示されています。(略)
(同)
この内容にはなるほど納得です.上の本から離れますが,「x×8」か「8×x」かに関しては,かけ算の順序は,ネットde真実で小中の接続について書いています.数式にすることの意義や,他の表現方法との比較については,かけ算の順序論争に立ち入るより前に,日本語・空間・数式・コードで文章化しています.
4. 今年の全国学力テスト
問題文と正答例は,毎日新聞からダウンロードして読みました.文科省経由で,ここから調査問題・正答例・解説資料*2を取得できます.
「かけ算の順序」に関わる問題は,もちろん見あたらないのですが,式の記述を見ると,興味深いものがあります.まず算数A大問3の
ある数を3でわったら,商が9であまりが2でした。
ある数を求める式を,下の1から4までの中から1つ選んで,その番号を書きましょう。
1 9÷3+2
2 9÷3−2
3 3×9+2
4 3×9−2
では,「9×3+2」や「9×3−2」「3×9+2」や「3×9−2」を選択肢に入れないのは意図的なのだろうなあと感じました.そして数学B大問1に出てくる式
(目標心拍数)=88−0.4×(年齢)+0.6×(安静時心拍数)
は,線形結合*3…じゃなかった,定数88があるので非斉次の式になっているなあと思ったりしました.
*1:これは中学校の教師向けに書かれた文章と思われます.
*2:なぜか解説資料の冒頭だけ「平成24年4月17日に実施した「平成25年度全国学力・学習状況調査」の…」となっています.
*3:「0.4×(年齢)」のうち,年齢が変数になり,0.4はその係数です.「0.4に年齢をかける」ではなく,「年齢を0.4倍する」です.もし単位を添えて考えるなら---一般に心拍数は単位なしですが---,「0.4(回/歳)」となります.「0.6×(安静時心拍数)」についても「安静時心拍数を0.6倍する」です,係数0.6の単位は,「0.6(回/回)」と書くことができます.