いきなりですが問題です.
どうして(-3)×(-2)=6となるのか,説明してください.
こういう説明問題で,次のような書き方は,おそらく,期待されていません.
- 3×2=6の両辺に-1を2回かけると,(-1)×(-1)×3×2=(-1)×(-1)×6.左辺は交換法則と結合法則により,(-1)×(-1)×3×2={(-1)×3}×{(-1)×2}=(-3)×(-2).右辺は6.ゆえに(-3)×(-2)=6(証明終)
ツッコミどころは,a=bならば-a=-bという性質や,正負の数を対象とした乗法の交換法則・結合法則を,証明なしに使っていいのかというところです.とはいえ,正解にしていいか,不正解あるいは減点とすべきかは,出題*1から採点までのプロセスにおいて,どのような取り決めがなされているかによります.
そういった代数的な定理の証明によらず,マイナスかけるマイナスはプラスに,そして(-3)×(-2)=6になることを説明するには…いくらでも食べられる,おいしい料理を用意しましょう*2.私がそれを1分間に3皿食べるとすると,2分間では3×2=6で6皿食べることになります.それだけ食べた時点を基準とすると,その2分前には,在庫は3×2=6で6皿分多いとなります.そこで,残りのお皿の変化に着目したプラスとマイナス*3と,時間のプラスとマイナスをあてはめると,(-3)×(-2)=6と言えます.しかし2種類の正負の数量を必要とし,誤解を招きやすそうです.
また別の手段は,数直線です.次の2冊の本は,負の数のかけ算の説明に,数直線を用いています.
主要部は次のとおりです.
そうなんです。では,負の数のかけ算とは何だろう。まずは
(-2)×3
のような,かけられる数が負,かける数が正のかけ算の意味を考えてみましょう。
女の子 答えは(-6)だよね。
男の子 負の方向へ2進むのを3回繰り返す。
豚 マイナス2の3個分。
(『生き抜くための数学入門』p.38)
3秒前,すなわち,-3秒後には,木よりも西の方向84m,すなわち,-84mのところを走っていました。
(+28)×(-3)=(−84)
(『中学数学再入門』p.34)
『生き抜くための数学入門』ではマイナスかけるプラスから入っています(本文では,その次はプラスかけるマイナスとなる2×(-3),そして両方ともマイナスの(-2)×(-3)と見ていきます).男の子の発言は,累加を表します.負の数の累加も,かけ算で表すことができるという考え方が,そこには含まれています.
一方,『中学数学再入門』の,負の数のかけ算の最初は,プラスかけるマイナスです.引用のあとは,かける数を1ずつ,3まで増やし,それぞれのかけ算の式と答え,その解釈を示しています.マイナスかける(-3から3まで)の式は,p.37に並んでいます.(-28)×(-3)=(+84)を含む,マイナスかけるマイナスの式は,その次のページです.
(+28)×(-3)=(-84)に話を戻すと,式を並べる都合として,この式から始まっていますが,小学生のかけ算の連携あるいは意味の拡張を図ろうとするなら,(+28)×(+3)=(+84)からスタートし,かける数を1ずつ減らしていくのが,分かりやすいように思えます.そこでは,小学校学習指導要領解説 算数編では第3学年で学習するという等式,a×(b±1)=a×b±aを用いることになります.aおよびbがプラス・マイナス・ゼロのいずれであっても成立するという考え方です.
ここまで2回,「考え方」と書きましたが,先に書いたほうは定義,あとに書いたほうは定理となります.ただしいずれも,それまで(小学校の範囲の演算)の拡張になりますので,拡張する前の状況で分かっている性質と矛盾することがないか,確かめることも,実は必要だったりします.
2冊の違いは,2次元平面を使って,次のように表すことができます.便宜上,x軸をかけられる数,y軸をかける数としています.
『生き抜くための数学入門』では,プラス×プラスを既知とし,マイナス×プラス,プラス×マイナス,そしてマイナス×マイナスの答えと見ていっています.
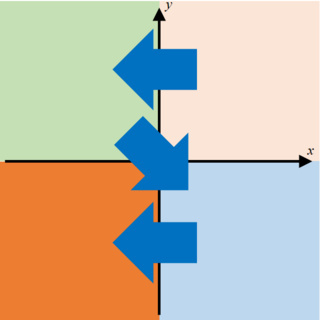
それに対し『中学数学再入門』では,プラス×プラスを既知とし,プラス×マイナス,マイナス×プラス,そしてマイナス×マイナスという順番です.
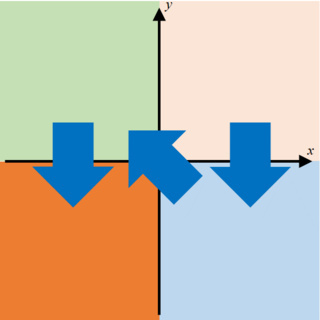
このように,流れは異なりますが,2つには共通点もあります.マイナス×マイナスがプラスになることを説明するときに使う数は,整数を用いており,小数や実数は使いません.もう一つは,かけられる数とかける数の違いに注意しながら,議論を進めているところです.交換法則は現れません.2×(-3)と(-2)×3,あるいはa×(-b)と(-a)×bがが等しいのは,別々の理由でそのかけ算の答えが-6あるいは-abになるため,と言えます.
昨今の「かけ算の順序論争」を踏まえると,小学校高学年になったら,あるいは中学の数学では,かけられる数とかける数の違いなんてないんだよ,というのでは,負の数のかけ算の説明で苦労することになるわけです.中島(1968)では,ラパッポルト氏による反論を紹介する形で,「アレイでも,(-3)×(-4)の説明はできない」と書いています.
とはいえ今回の話を,非順序派への攻撃の材料として使うのではなく,乗法には〈乗数と被乗数が区別される文脈〉と〈乗数と被乗数を区別しない文脈〉(乗数効果より)という大まかな分類が,算数でも数学でも,日常生活にも存在するんだということを,今後も呼びかけていくとします.
『生き抜くための数学入門』は,今月9日に学外の図書館(農民カフェ絆で昼食)で見かけた本で,その後,Amazonで取り寄せました.『中学数学再入門』は書店で購入しました.
はてブとコメントありがとうございます.
ROYGB 縦−3センチで横−2センチの長方形の面積は6平方センチというのはダメか。縦3センチで横−2センチだったら面積がマイナスになる。
符号付きの面積といえば,定積分を使いたいところです.f(x)=3,g(x)=-3(どちらも定数関数)を用いると,
が言えます(定積分の下端が上端より大きいときの扱いは「規約」(wikipedia:積分法)によります).そして最後の定積分が,(-3)×(-2)=6に対応します.
一般には,f(x)+g(x)=0と,いくつか条件を設けた上で,
となります.

