いきなりですが問題です.
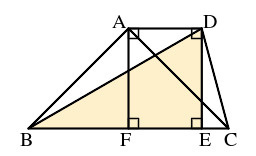
下の図の四角形ABCDで,AD//BC,AB=AC,BD=BC,∠BAC=90°であるとき,∠ABDの大きさを求めなさい。
- 中学数学の範囲内で,理由を説明する.
- ワンライナーで,答えとなる値だけを出力する.
さっそくですが解答です.∠ABD=15°です.
まずは中学数学の範囲内で検討します.三角形ABCは,∠A=90°の直角二等辺三角形ですので,∠ABC=∠ACB=45°です.三角形BCDは,BD=BCの二等辺三角形ですので,∠BCD=∠BDCです.またAD//BCより,平行線の錯角に留意すると,∠DAC=∠ACB=45°,∠ADB=∠DBCです.
これだけ,角度の情報が分かれば,一つの三角形に着目し,内角の和が180°になることを使って,∠ABDが求められそうにも思います.そこで,∠ABD=x°とおいて,三角形ABDの内角の和を考えてみますと,∠BAD+∠ABD+∠ADB=180°のうち,∠BAD=∠BAC+∠CAD=135°,∠ABD=x°はいいとして,ちょっと困るのは,∠ADB=45°−x°となることです.そうすると,∠BAD+∠ABD+∠ADB=180°の式の左辺に代入すると,xが消えてしまい,式は180°=180°となってしまいます.
別のアプローチをとります.AとDから,線分BCに垂線を引き,BCとの交点をそれぞれFとEとします.

AF⊥BC,DE⊥BCと書くこともできます.線分FEは線分BCの一部であることにも注意します.
そうすると,AD//FEですので,四角形AFEDは,すべての角が直角の長方形となります.長方形の向かい合う辺の長さは等しいことから,DE=AFを得ます.
辺の長さについて,三角形ABCが直角二等辺三角形であることに注意すると,AF=BF=CF=BCが言えます.そして,DE=AF=
BC=
BDとなります.
ここで三角形BEDに着目します.
∠BED=90°の直角三角形です.加えて,DE=BDであることから,三角形BEDは,1辺の長さがBDの正三角形の半分の形(正三角形を線分BEでカットしてできる図形)であることが分かります.三平方の定理を学習した後なら,DE:BD:BE=1:2:
と表現するのが,分かりやすいでしょうか.
そうすると,∠DBE=30°(正三角形の一つの角の半分)であり,∠ABD=∠ABC−∠DBE=45°−30°=15°として,求めるべき角の大きさが計算できました.
ワンライナーは,Rubyで実行することにします(本日の記事の図形も,Rubyで座標を求めて,作図したのでした).その前に,AからDまでの4点を,平面座標で表すことにします.Bを原点とします.つまりB(0,0)です.また,C(1,0),A(,
)とします.
Dの座標は計算で求めます.D(x,y)とおいたとき,AD//BCより,DのY座標はAのY座標と等しく,y=です.次に,BD=BC=1であり,BD=
ですので,既知のyの値,およびx>
を考慮すると,x=
となります.D(
,
)というわけです.
ではワンライナーを示します.以下のコマンドで「15」を出力します.
ruby -e "puts ((Math.atan2(0.5,0.5)-Math.atan2(0.5,Math.sqrt(3)/2))/Math::PI*180).round"
Math.atan2は,yとxを引数にとり,y/xの逆正接(アークタンジェント)の値を弧度法で返します.前者のMath.atan2の呼び出しは,∠ABCに対応する角の大きさを,また後者は∠DBEを,それぞれ求めることになります.引き算してから,弧度法を度数法に変換するためのわり算とかけ算を行います.そのままだと,手元の実行環境では「14.999999999999996」と出力してしまうので,四捨五入を行うroundメソッドを入れています.
なお,問題をもらった際には「中3生の模試の問題なのですが,私はもちろん,現役国公立大生や数学科の大学生誰1人解けないという超難問(笑)」が添えられていました.そんなことないでしょう.教科書レベルとは言いがたいですが,中学数学を教えている,塾の先生や家庭教師なら,問題を見て1分もかからずに,生徒に解き方を説明できるのではないかと思います.
さらに言うと,直角二等辺三角形と,30°60°90°の直角三角形の性質を理解していれば,小学生(たとえば私立中学の受験生)でも解くことのできる内容です.
(最終更新:2017-10-10 朝.タイトルを「∠ABDの大きさを求めなさい」から変更したほか,細部を修正しました)
