東大阪市立小阪小学校、2018年春に実施した7段ピラミッドです。これと同じものを今年もやるのでしょう。極めて危険です。即中止してください。最下段中央の最大負荷量は4.8人分です。https://t.co/2ru2L9FnuJ pic.twitter.com/JJdFgaWCOr
— Yutaka Nishiyama (@ma85003) 2019年5月31日
フォローありがとうございます。小阪小学校の7段は画像からみて、上4段が平面型、下3段が立体型(奥行きがある)に見え、平面型7段に近いと判断しました。ところが立体型の7段だといって、計算が間違っているというコメントがあり困っていました。奥行きと言っても2列程度です。 https://t.co/DpQ6i5LliB
— Yutaka Nishiyama (@ma85003) 2019年6月1日
人数が増えれば最大負荷量は小さくなるはず,と思いながら,平面型(俵型,三角形型)と立体型(三角錐型)との混合によるピラミッドの組み方を,検討してみました.
下が平面型・上が立体型というのは,構成できませんので,下の何段かを立体型,それより上を平面型とします.とりあえず7段で考え,他の段でも適用できるようにします.
7段の立体型の構成については,『組体操指導のすべて―てんこ盛り事典』p.145に図があります.横から見た構成で,左側が正面になります.
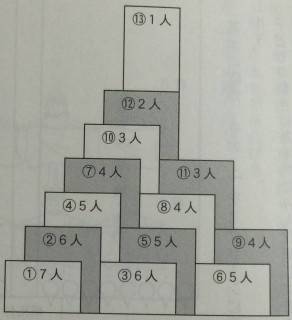
構成の手順は,https://github.com/takehiko/gf/blob/master/text/trigonal.txtの「7段の三角錐タイプのピラミッドをつくるには、55人が協力して行います。」から読むことができます.
図をPowerPointで再構成し,PNG画像にしました.

正面に見えない人を取り除いて,①の人で上の人をすべて支えるとなると,平面型です.

この平面型について,下から2段目だけ,足を地面につけて中腰の姿勢になるのが「足つき」で,組体操のピラミッド(俵型・三角錐型・クイック・足つき)についてで紹介してきました.

立体型に戻ります.この構成から,⑫の人は,中腰ではなく四つんばいになり,膝を⑩の左右に乗せることにします.
そうすると,⑪と⑨を取り除くことができます.構成は以下のとおりです.⑩を筆頭とする5段の立体型ができるので,「下5段立体型」と呼ぶことにします*1.

同様に,上の者で平面型を作るようにすると,7段を維持したまま,ほかのピラミッドを得ることができます.立体型・平面型と合わせて,GIFアニメーションを作りました.

ではそれぞれの負荷量計算といきましょう.最後のコミットが3年前だった,gfのコードを見直して,計算を試みました.今回の件の計算ができるコードを,すでにコミットしています.
以下はgf内の表記を使用します.「平面型」ではなく「俵型」,「立体型」は「三角錐型」,そして「負荷量」のかわりに「荷重」です.
gf/lib/gf/triangle2.rbの中に,build_pyramid_triangle2という名前で,「足つき」のピラミッドを構成するメソッドを,以前に定義していました.その内容を見直しながら,build_pyramid_triangle_trigonalという名前のメソッドを,同じrbファイルに新たに定義しました.引数は,段数(lev)と,下から何段目までを三角錐型にするか(lev2)で,それぞれデフォルトは3と1です.
コーディングにあたり,lev2の値が1のときは,俵型と同じに,2のときは足つきに,lev-1のときには三角錐型と同じになるようにしました*2.
7段(lev=7)で,演技者の体重をすべて1とし,lev2を1から6まで変えてみて,実行したところ,結果は以下のようになりました.
$ for i in 1 2 3 4 5 6; do echo -n "lev=7, lev2=${i}: "; ruby lib/gf.rb -u 7,$i; done
lev=7, lev2=1: 28 persons, total_weight=28, max_load=4.8125, max_rate=4.8125 (name=1.1.4, weight=1, load=4.8125)
lev=7, lev2=2: 28 persons, total_weight=28, max_load=3.8125, max_rate=3.8125 (name=2.1.4, weight=1, load=3.8125)
lev=7, lev2=3: 34 persons, total_weight=34, max_load=3.125, max_rate=3.125 (name=3.1.3, weight=1, load=3.125)
lev=7, lev2=4: 39 persons, total_weight=39, max_load=2.1875, max_rate=2.1875 (name=2.2.3, weight=1, load=2.1875)
lev=7, lev2=5: 48 persons, total_weight=48, max_load=1.8925, max_rate=1.8925 (name=2.2.3, weight=1, load=1.8925)
lev=7, lev2=6: 55 persons, total_weight=55, max_load=2.40612, max_rate=2.40612 (name=1.3.3, weight=1, load=2.40612)人間にとって読みにくいので,Excelで出力しました.
$ for i in 1 2 3 4 5 6; do echo "7,${i}"; ruby lib/gf.rb -u 7,${i} -x triangletrigonal_7_${i}.xlsx; done 一つの構成につき一つのワークシートで出力されます.1個のファイルに各ワークシートを入れ,概要を追加したExcelファイルが,https://drive.google.com/file/d/1sOJ0UHRCIU1v_MBFuVq8nwlbAxU3fURG/view?usp=sharingよりダウンロード可能です.概要以外のワークシートの見方についてはhttps://github.com/takehiko/gf/tree/master/excelをご覧ください.
概要は以下の通りです.上記の読みにくい実行結果に,「正面から見えない人の数」「荷重1以上の人数」「荷重2以上の人数」の列を加えて,表にしました.

6つの組み方の中で,「下5段立体型」の最大荷重が,最も小さくなっているほか,荷重2以上(自分の体重の2倍以上の荷重がかかる人)がいません.
三角錐型(立体型)7段の55人より,下5段立体型の方がなぜ,最大荷重が小さくなるのか,直感的な説明は思いつきません.とはいえ,上で「人間にとって読みにくい」と書いた出力を見て,気になるのは,最大荷重がかかる人が,三角錐型(lev=7, lev2=6)では"name=1.3.3"すなわち最下段(四つんばい)の前から3列目の真ん中の人なのに対し,下5段立体型(lev=7, lev2=5)では"name=2.2.3"で,下から2段目(中腰)の前から2列目の真ん中となる点です.俵型の最大荷重のかかるのは,最下段の中央なのですが,組み方によっては下から3段目の人に最大荷重がかかるというのもあります.
ところで,https://www.mbs.jp/news/kansainews/20190531/GE000000000000028001.shtmlでは「6段で実施する」となっていますが,levを6,lev2を1から5まで変えて実行したところ,立体型の場合を除いて,荷重の減少は見られませんでした.7段に戻って,「-m 4 -z s6 -s 12345」というオプションを入れて,演技者ごとの体重のばらつきを考慮してみたところ,荷重は下がり,下5段立体型の最大荷重(自重に対する割合)は1.45267と出ました.
関連: