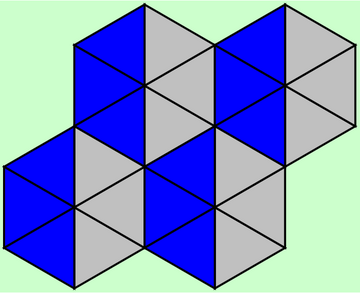
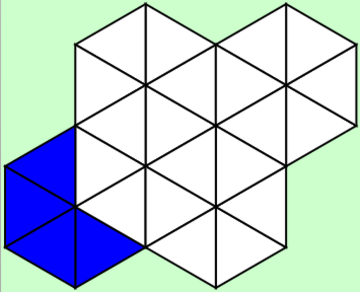
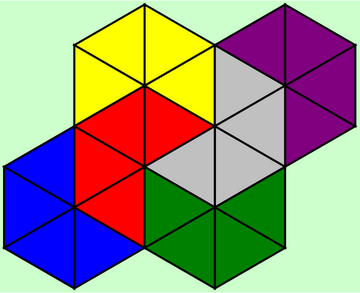
いきなりですが問題です.まずは下の画像をご覧ください.
正三角形が全部で24個あります.「4個ずつ,6つのまとまり」が分かるよう,三角形に色を塗ってください.
元ネタは以下の本のpp.54-57です.色塗りではなく,太く囲ったり,三角形の中に丸囲み数字を書き入れたりすることで,「まとまり」を表しています.
図形に色を塗るのは,以前にSVG画像を作っています.
今回の問題用に,作り直しました.*1
そのままブラウザ上で動作します.画像が表示されなかったら,ページ左上の「Run」を押してみてください.
三角形をクリックすると,青→緑→赤→黄→紫→灰→白→…と色が変化します.
これを活用して,まずは「6個ずつ,4つのまとまり」が分かるよう,色を塗ると,例えば次のようになります.
「3個ずつ,8つのまとまり」は,次の通りです.
「4個ずつ,6つのまとまり」を作る前に,「4個の(1つの)まとまり」を,以下のようにします.正六角形の3分の2の部分です.
これと同じ形状になるよう,残りを塗り分けると,以下のようになります.
ところで,「4個ずつ,6つのまとまり」を,小学校算数で学んだ式に表すと,4×6です.「6個ずつ,4つのまとまり」は6×4,「3個ずつ,8つのまとまり」は3×8です.
積が24になる,かけ算の九九の式には,あと一つ,8×3があります.「8個ずつ,3つのまとまり」を,冒頭の図から得る(塗り分ける)ことができるか…
というと,これまでと同じようにはできません.8つの三角形を選んで,1つの図形とし,合同になるよう3つの図形で,もとの(正三角形24個で構成される)図形を分割することができないのです.この図形は3回対称(wikipedia:回転対称)ではありません*2.
『四則計算』p.56では,先生(T)の質問と児童(C)の発言が,以下のように書かれています.
T: 三角形の数は,他にどんな式で求めることができますか。
C: 三角形の数は24個なので,3×8を反対にした8×3で求められます。
C: 6×4を反対にした4×6でも求められます。
C: 4×6は,「一つ分の大きさ」にした矢印のような図形が6つ,敷き詰められます。*3
C: 8×3はこの模様に合いません。「一つ分の大きさ」の形が変わってしまいます。
C: 「一つ分の大きさ」は,数も形も同じじゃないとまとまりと言えません。そのまとまりの中に三角形がいくつあるのか,そのまとまりが模様にいくつあるのか,かけ算の式で求めることができます。
与えられた図形から「mずつ,nのまとまり」は見つけられるが「nずつ,mのまとまり」を見つけることが困難な状況が,他にないか,探してみると,サブブログで図にしていました.
学校図書『みんなと学ぶ 小学校 算数 3年上』p.24の問題です(略)
他と見比べて分かるように,同心円上の丸の数は8つです。丸をつなぐ線はいずれも水色です。ということで式は,「3×8=24」と「8×3=24」が思い浮かびます。同一直線上に並んだものを,1つ分とみなすと,「6×4=24」という式で表すこともできます。
「4×6」となるよう,同じになるように丸を分けるのが困難です.図形としてみると,6回対称ではありません.
*1:SVGファイルも動作し,gistに登録しましたが,ブラウザ上でうまく動作しなかったため,リンクは差し控えます.
*2:ただし,「図形をn個の合同な図形に分割できること」と「図形がn回対称であること」は同値ではありません.今回の図形は,8個の合同な図形に分割できますが,8回対称ではありません.
*3:「敷き詰める」は,小学校学習指導要領 算数の第2学年に含まれていますhttps://w3id.org/jp-cos/8250225500000000.『小学校学習指導要領(平成29年告示)解説算数編』p.120では,長方形の敷き詰めが図になっています.